Fig. 1
An example of the stimulus artifacts removal in a stimulation task. (a) The first figure shows the communicated sEMG, and the other one is the filtered result. (b) In order to see this result clearly, this is got from the part surrounded by the red rectangle maximized in (a)
2.4 Partial Directed Coherence
To represent the Granger causality on a frequency domain method, partial directed coherence is proposed [13].
Let x = (x(t)) t ∈ z , when x(t) = (x 1(t), ⋯, x n (t))′ is a stable n-dimensional time series that averages zero. Then a short p order VAR model as follows:
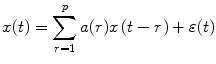
Let the pth order vector autoregressive model describes the set of simultaneously observed second-order stationary time series:
![$$ \left[\begin{array}{c} {x}_1(t) \\ {} \vdots \\ {} {x}_Q(t) \end{array}\right]={\displaystyle {\sum}_{k=1}^p{A}_k}\left[\begin{array}{c} {x}_1\left(t-k\right) \\ {} \vdots \\ {} {x}_Q\left(t-k\right) \end{array}\right]+\left[\begin{array}{c} {w}_1(t) \\ {} \vdots \\ {} {w}_Q(t) \end{array}\right] $$](/wp-content/uploads/2016/09/A315578_1_En_48_Chapter_Equ2.gif)
The linear relationship between x j and x i are described at the by the coefficients matrix A k kth past lag, and the ε(t) is a multivariate Gaussian white noise process.
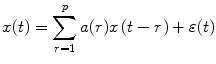
(1)
![$$ \left[\begin{array}{c} {x}_1(t) \\ {} \vdots \\ {} {x}_Q(t) \end{array}\right]={\displaystyle {\sum}_{k=1}^p{A}_k}\left[\begin{array}{c} {x}_1\left(t-k\right) \\ {} \vdots \\ {} {x}_Q\left(t-k\right) \end{array}\right]+\left[\begin{array}{c} {w}_1(t) \\ {} \vdots \\ {} {w}_Q(t) \end{array}\right] $$](/wp-content/uploads/2016/09/A315578_1_En_48_Chapter_Equ2.gif)
(2)
From the joint spectral density estimate x = (x(t)) t ∈ z through:
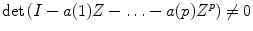
![$$ A_{k} = \left[\begin{array}{c@{\quad}c@{\quad}c} a_{1,1}(k) & \cdots & a_{Q,1}(k)\\ \vdots & \ddots & \vdots \\ a_{Q,1}(k)& \cdots & a_{Q,Q}(k) \end{array}\right] $$](/wp-content/uploads/2016/09/A315578_1_En_48_Chapter_Equ4.gif)
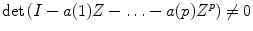
(3)
![$$ A_{k} = \left[\begin{array}{c@{\quad}c@{\quad}c} a_{1,1}(k) & \cdots & a_{Q,1}(k)\\ \vdots & \ddots & \vdots \\ a_{Q,1}(k)& \cdots & a_{Q,Q}(k) \end{array}\right] $$](/wp-content/uploads/2016/09/A315578_1_En_48_Chapter_Equ4.gif)
(4)
Do not like the original granger causality that is double variable time series, partial directed coherence is based on the treatment of multivariable autoregressive time series. To describe Granger causality relations, the concept of partial directed coherence is introduced. So for the autoregressive process of order p partial directed coherence are defined as follows:
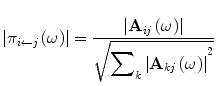
Condition (2) ensures that the denominator is always positive, so the equation can well define directional coherent. As can be seen from the definition, if and only if all the coefficients a ij (r) are equal to zero, |π i←j (ω)| for all frequencies ω do not exist, thus there is no Granger causal connection between x j and x i . This means that the partial directional coherent |π i←j (ω)| delivered a measurement for the directed linear influence in the frequency domain. Also, because Eq. 5 is a normalized form, therefore partial directional coherent takes value in [0, 1]. It compared the influence of the past for and the impact of the past with other variables, therefore, for a given signal source, partial directional correlation analysis can be arranged according to the intensity of the impact of variables.
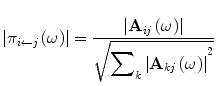
(5)
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree







