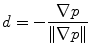Fig. 14.1
Automatic (in green) and manual (in red) delineation of brain organs at risk in radiotherapy. The segmented structures include optic nerves, eyes, brain stem and cerebellum (From Isambert et al. (2008))
Brett et al. (2001) were among the first to explicitly address the problem of missing correspondence in registration of tumor images. They suggested masking the cost function of a combined affine and non-rigid registration method. For this, a manual pre-segmentation of the lesion was required and could be used as a mask for the similarity criterion during the registration. A similar approach was chosen by Stefanescu et al. (2004). A confidence map with zero confidence for all voxels inside the pre-segmented tumor mask was used for the similarity metric during the registration process. Additionally, adaptive regularization was allowed in different tissue regions.
Dawant et al. (2002) placed small tumor seeds in the atlas at the patient’s approximate tumor location. Then, a non-rigid registration was performed, which simultaneously deformed the seeds in the atlas to approximately match the pre-segmented patient tumor. Commowick et al. (2005) employed statistical measures of anatomical variability for guiding the regularization during the registration process, where regions of low variability were more strongly regularized and regions of high variability, like tumor regions, could deform more. Chitphakdithai and Duncan (2010) used an indicator map to model different correspondence assumptions for various tissue classes. Registration was regarded as a maximum a posteriori (MAP) problem and solved in an expectation maximization (EM) framework, whereas the probability term of the transformation could be seen as a similarity metric.
A different idea is to incorporate a lesion model directly into the registration method, which allows for a decoupling of the deformations due to tumor growth and inter-subject variations. In this direction, Bach-Cuadra et al. (2004) suggested a model of lesion growth for atlas-based segmentation of tumor-bearing brain images. To this end, a simplistic radial lesion growth model was incorporated into a Demons-based non-rigid registration method. The lesion growth model modified a healthy atlas and adapted it to the tumor-bearing patient image. Despite having two distinct deformation models, this method relied on registration models only and did not include any kind of bio-mechanical tumor-growth simulation. Later, Bach-Cuadra et al. (2006) from the same group improved their previous method by replacing the SSD-based Demons registration algorithm with an optical flow method employing the more robust mutual information similarity metric, which allowed them to drop the assumption of a linear intensity correspondence relation between the two images. Niethammer et al. (2011) proposed a metamorphosis model, which combined two distinct deformations in order to jointly estimate a deformation in space and a change in image appearance. A global geometric deformation was employed to model changes in image appearance and local matching for considering the tumor was based on an image composition model in an LDDMM framework.
Methods Combining Tumor Growth Modeling with Registration for Atlas-Based Segmentation
Another idea to circumvent the problem of a missing correspondence between the atlas image of healthy individuals and the pathological patient image is to seed the atlas with a tumor before applying the non-rigid registration. Most of the underlying approaches make use of a bio-mechanical tumor-growth model that simulates patient-specific tumor growth in the atlas image, and they finally apply a standard non-rigid registration method to the modified atlas image.
Kyriacou et al. (1999), the first ones to suggest this type of approach, assumed a uniform strain of the tumor and non-linear elastic behavior of the surrounding tissues. In a first step, they shrank the tumor in the patient image to obtain a simulated healthy patient image. Then, the tumor shrinkage process was inverted by performing tumor growth on the registered atlas using a regression method. This allowed them to obtain a patient-adapted atlas including pathology in a final step. Mohamed et al. (2006) grew the tumor in the atlas according to the pathological patient image, instead of shrinking the tumor first. The final adaptation of the modified atlas to the patient image was achieved with a non-rigid registration method. To handle the significant computational cost of the tumor growth modeling in 3D, they employed an approach based on a statistical model using principal component analysis (PCA). For each available case, they estimated the most likely parameters and applied the deformation using the pre-built statistical model. Zacharaki et al. (2008) improved this approach by implementing a multi-resolution framework for registration of brain tumor images. In their so-called ORBIT method, they also used a statistical model of tumor-induced deformation, but they embedded it into a hierarchical framework for parameter optimization. Local information was incorporated into the tumor growth model and the registration methodology was improved. In a further step, the same group improved their tumor growth model compared to the previous method (Zacharaki et al. 2009). They dropped the need for a simplified PCA-based tumor growth model while still achieving computational efficiency. To this end, they employed a piecewise Eulerian tumor mass-effect simulator with a uniform outward-pushing pressure model for the bulk tumor. Parameter optimization was parallelized for further speed improvements.
Recently, researchers from the same group built upon the previous methods by making improvements to the tumor growth model. Instead of considering only bio-mechanical mass effects with a simplified pressure model, they proposed a more sophisticated coupled physio-mechanical model. In GLISTR, Gooya et al. (2011a), employed a diffusion–reaction model for tumor growth, which was coupled with an Eulerian finite element method (FEM) for simulating the mass effect. They operated on multi-sequence images to obtain a probability map of the different tissue classes using classification techniques. In the atlas, a patient-specific tumor was grown and a Demons-like algorithm was finally used for the atlas-to-patient transformation. For this, the tissue probability map output from the classifier was used in the cost function. The process was formulated as an EM problem, which jointly estimated tumor growth parameters and the spatial transformations to adapt the atlas to the patient image. This resulted in a large optimization problem, which had to be solved. In a next step, Gooya et al. (2011b) dropped the requirement for pre-classification and proposed a joint segmentation and registration model, which also included tumor growth. This was again formulated in an EM framework for joint estimation of tumor growth parameters and the deformation field for registration. The posterior tissue probabilities, which had been derived from the deformed atlas, yielded the segmentation of the patient image.
Our own research was inspired by methods which suggested combining tumor-growth modeling for the tumor mass effect and the establishment of initial correspondence between atlas and patient image with advanced non-rigid registration. In our method for atlas-based segmentation of tumor-bearing brain images, we explored two different lines of research: On the one hand, we worked on a simplistic but fast method for atlas-based segmentation, and on the other hand, we explored a more sophisticated but computationally more demanding approach.
For the simplistic but fast approach, in Bauer et al. (2011a), we developed a method, that segmented the healthy tissues surrounding the tumor in a brain image by atlas-based segmentation. These tissues included cerebrospinal fluid (CSF), gray matter (GM) and white matter (WM). The method used a simplistic but computationally fast bio-mechanical tumor growth method to first grow a patient-specific tumor in the atlas and then deform the modified atlas to match the patient image using a non-rigid Demons registration method. We relied on a pre-segmentation of the tumor as an input and performed automatic skull-stripping in a pre-processing step. Then, we aligned the atlas to the patient image using an affine transformation model. From there, we defined a tumor seed in the atlas which was located in the center of mass of the patient tumor. Subsequently, a mesh-free method based on Markov Random Fields (MRF) was used for modeling the tumor-mass effect. We chose a radial expansion model which was propagated by an MRF on the deformation field and which was bio-mechanically justified because it considered the Young’s modulus of different brain tissues during tumor expansion. Tumor expansion was formulated as an energy minimization problem in an MRF context which was solved using the iterated conditional modes (ICM) algorithm. The ICM algorithm had the advantage that it could be parallelized very easily and it was implemented on a massively parallel graphics processing unit (GPU); this led to significant speed improvements. After tumor growth modeling, the final adaptation of the modified atlas to the patient image was done using an ITK implementation (Ibanez et al. 2005) of the Diffeomorphic Demons non-rigid registration method (Vercauteren et al. 2009). Figure 14.2 illustrates the pipeline. A tumor seed was automatically selected in the center of mass of the patient tumor and the tumor was grown in the atlas, deforming the surrounding tissues, before the final non-rigid registration was applied. The results were analyzed on four T1-weighted images from the ContraCancrum database (Marias et al. 2011) and four synthetically generated brain tumor images with a well-defined ground truth (Prastawa et al. 2009). Quantitative evaluation was performed using the Dice similarity coefficient, which measures the overlap with the ground-truth segmentation. The Dice coefficient can range from 0 to 1, with 0 indicating no overlap and 1 indicating perfect overlap. The algorithm achieved Dice coefficients between 0.7 and 0.82 for the relevant tissue CSF, GM and WM within a total computation time of less than 30 min on a GPU.
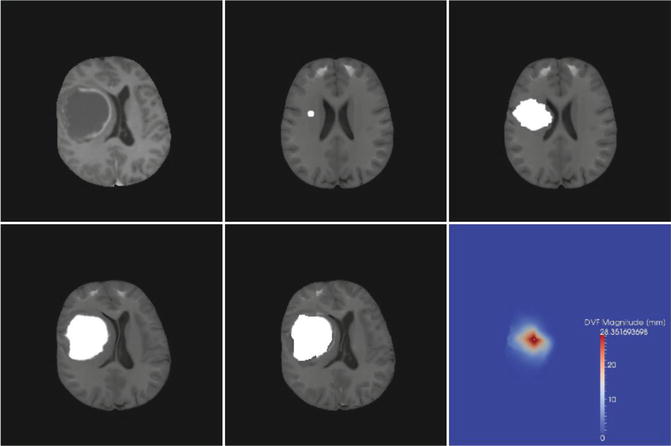

Fig. 14.2
Results of atlas-based tissue segmentation illustrated on one axial slice of a patient image. Top row left to right: patient image, seeded atlas after affine registration, deformed atlas after tumor growth. Bottom row left to right: modified atlas after final non-rigid registration, tissue checkerboard of final result and the magnitude of the displacement field resulting from the tumor mass effect simulation (From Bauer et al. (2011a))
For the biophysically more realistic approach, in Bauer et al. (2012), we explored a computationally more demanding method for multi-scale tumor growth modeling in atlas-based segmentation of tumor-bearing brain images. We chose the same pipeline as in the previous method that included automatic skull-stripping of the patient image, affine registration of the atlas, seeding the atlas with a physically realistic tumor seed in the center of mass of the patient tumor, tumor growth simulation to model the tumor mass effect, and final non-rigid registration. The difference was that, in this case, we replaced the simplified purely bio-mechanical tumor growth model with a more sophisticated tumor growth model which considered multiple scales ranging from the microscopic cellular level up to the macroscopic bio-mechanical level. To this end, a discrete-entity, discrete-event cellular-level based oncosimulator (Stamatakos et al. 2010) focusing on biological phenomena like cell-cycling and apoptosis was coupled with a bio-mechanical stress/strain simulation (May et al. 2011) which could provide pressure gradient information. Since the limit of applicability of the standard Lagrangian formulation of structural mechanics was reached under large tumor-induced deformations, the linear-elastic model was solved in an Eulerian implementation of FEM. Thus, the calculation was performed on a fixed geometrical mesh and material properties were advected to neighboring elements upon deformation. Furthermore, this allowed for operating directly on the voxel mesh obtained from the image, eliminating the need for complex mesh generation procedures. The cell simulator required information on the direction into which new tumor cells would spread. This direction could be decided based on the pressure of the surrounding tissues. The pressure was obtained from the mechanical simulator which in turn required information about the expansion of each geometrical cell. This was calculated from the cellular proliferation model. The direction of least pressure 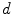 was calculated based on the negative gradient
was calculated based on the negative gradient
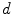 was calculated based on the negative gradient
was calculated based on the negative gradient