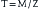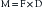Chapter 136 Basic Biomechanically Relevant Anatomy
Biomechanics
Vectors, Scalars, Bending Moments, and the Instantaneous Axis of Rotation
A vector is a force oriented in a fixed direction in three-dimensional space (as defined by the right-handed Cartesian coordinate system previously discussed). It possesses both magnitude and direction (i.e., force and velocity), and it may be broken down into its component vectors. A scalar is a quantity that is direction independent and possesses only magnitude (i.e., time, volume). A bending moment occurs when a force acts on a lever or moment arm. A bending moment, when applied to a point in space, results in a tendency to rotate about an axis. When these principles are applied to a vertebral body, the three-dimensional axis about which a bending moment causes the body to rotate; this is known as the instantaneous axis of rotation (IAR). The IAR is the axis about which a vertebral segment rotates at any given instant, and the IAR itself does not move during this instant of rotation or translation. It may be considered a fulcrum about which a segment moves. When a body moves in a plane, there is a point in the body or some extension of it that does not move, and the axis that passes perpendicular to the plane of motion and through this point is the IAR (as defined by White and Panjabi1). The IAR becomes the center of the Cartesian coordinate system used to define the motion. The IAR is dynamic, and as spinal movement occurs, the IAR of each involved segment moves. The location of the IAR depends on the manner in which it is determined and the theoretical foundation on which it is based, and it is therefore subject to error.
Free Body Analysis
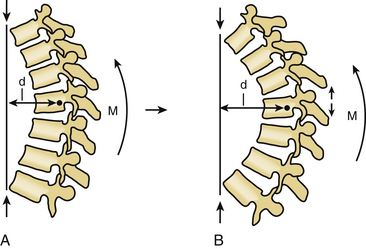
Free body diagrams use the forces, moments, and IAR on various anatomic structures to isolate those forces and assign vectors, so that all the forces are represented. In that way, complex problems can be reduced to their component parts. It is then possible, for example, to determine the force necessary to stand upright or the increase in paraspinal and gluteal force required by leaning forward as in kyphosis. These diagrams help one to understand these complex problems. They also form the basis for understanding why tension band disruption may lead to kyphosis in either the cervical or lumbar spine. As the moment arm moves forward and increases, even small amounts of kyphosis (or loss of lordosis) can have large effects on the forces acting on the spine (Fig. 136-1).
Newton’s Laws
Spine surgery involves the application of force to the spine. Fundamental to understanding the stresses withstood by the spine is the concept of action and reaction.2 Newton’s three laws of motion describe how objects respond to external forces.
1. The first law is the law of inertia, which states that if an object is subject to no net force, it maintains a constant velocity.
2. The second law is the law of superimposition of forces, which states that the momentum of an object is equal in magnitude and direction to the vector sum of the forces acting on it.
3. The third law is the law of conservation of momentum. which states that when two objects collide, the overall momentum is constant such that for every action there is an opposite but equal reaction.
As the spine is subject to various loads, force couples are created (based on the third law of motion), and the vertebral segments may fail. When applying forces to the spine, these same concepts need to be considered. All instrumentation will fail in time, and therefore the bony alignment must respect the body and gravitational forces or it will fail more quickly. The biomechanical environment must maintain a load balance between the implant and tissue environment to improve implant longevity.
Hooke’s Law and Stress-Strain Curves
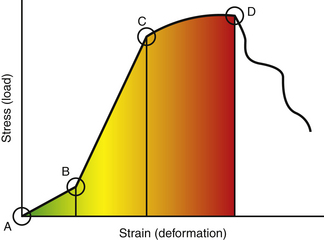
When external forces act on a solid at rest, the solid is deformed. According to Hooke’s law, for small displacements, the size of the deformation is proportional to the deforming force. For solids within the elastic zone, the relationship between deformation and force is linear. To make sense of Hooke’s law then as it applies to the spine, the concepts of stress-strain curves and deformation need to be expanded. Deformation of a solid can be either elastic or plastic. Elastic and plastic are defined by recovery once the deforming force is removed, and they exist on a spectrum that can be best illustrated with a deformation curve (Fig. 136-2). When a solid is subject to an external or deforming force, Hooke’s law applies only when the load and deformation occur within the elastic zone of the solid. The elastic zone is defined by elastic deformation, when a solid totally recovers after removal of a stress. Deformation continues to be proportional to the deforming force until the elastic limit of the solid is reached and the linear relationship between force and deformation no longer exists. Beyond the elastic limit of a material is the plastic zone, and this is the zone in which the solid acquires permanent deformation and does not completely recover once the stress is removed. As force continues to be applied, eventually the point of failure is reached. On a stress-strain curve (see Fig. 136-2), the area under the curve represents the amount of energy absorbed and the ultimate strength of a material (amount of energy required to reach failure). The neutral zone is an area of nonengagement where force is applied but deformation is minimal. It precedes the linear area of the curve.
Elastic Modulus
There are three types of elastic moduli:
1. Young’s modulus, which measures the elastic properties of an object when it is stretched or compressed
2. Shear modulus, which measures the shear deformation that occurs when transverse forces of opposite direction are applied at opposing faces of an object
3. Bulk modulus, which measures the deformation that occurs when a solid is squeezed
Section Modulus and Moment of Inertia
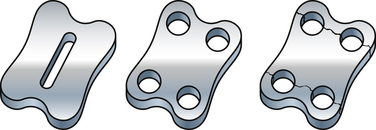
The section modulus is a concept that is calculated and used to define the strength of an object. It is applicable here with regard to spinal implants and instrumentation as an indicator of the overall strength and, more importantly, potential failure of an implant. The section modulus or strength of a screw is exponentially related to the diameter of the screw. As this diameter increases, the strength increases by the power to the fourth. This concept is also applicable to plate design. The strategy for hole placement for screws must be carefully designed because the holes reduce the section modulus. This then causes failure of the plate at a lower load (Fig. 136-3).
where T is stress, M is bending moment, and Z is section modulus. The bending moment (M) is also defined by an equation:
where M is bending moment, F is the force applied, and D is the distance of the moment arm through which the force is applied.
Basic Biomechanics of Bone
Bone fractures and the fracture patterns also follow the magnitude and direction of the forces applied. Wolff’s law, a theory developed by the German anatomist/surgeon Julius Wolff (1836–1902), states that bone adapts to imposed stress. If loading on a particular bone increases, the bone remodels itself over time to become stronger to compensate for greater load requirements.3
Rapidly applied loads to the spine may result in failure of the ligaments or bone, or both. The direction of force application, magnitude, and bony integrity all play a role in the fracture pattern and displacement. Several distinct failure patterns can be observed.
Avulsion Fracture
These occur as a result of the strong ligamentous attachments to the spine. The ligaments, which are strongest in tension due to their high collagen content, can avulse bony fragments (Table 136-1). An example of this is the bony avulsion seen with Jefferson burst fractures, where the transverse ligament avulses a portion of the lateral mass of C1.
TABLE 136-1 Spinal Ligament Forces
| Ligament | Cervical (N) | Lumbar (N) |
|---|---|---|
| ALL | 112 | 450 |
| PLL | 75 | 324 |
| ISL | 240 | 125 |
| SSL | 36 | 150 |
ALL, anterior longitudinal ligament; ISL, interspinous ligament; PLL, posterior longitudinal ligament; SSL,supraspinous ligament.
From White AA, Panjabi MM: Clinical biomechanics of the spine, ed 2, Philadelphia, 1990, Lippincott, p 22.
Flexion-Distraction Fracture (Chance Fracture)
These fractures occur with a significant flexion moment, with the axis of rotation anterior to the spinal unit. This large moment (mass times acceleration times moment arm) results in a tremendous extension force to the spine. The mode of failure is tensile through the posterior elements and then progresses through the vertebral body. The classic example of this type of injury was described by Chance in 1948 and bears his name.4 The bony or ligamentous component of the fracture is determined by the difference between the tensile strength of the bone and ligaments, and the force travels through the path of least resistance.
Burst Fracture
The burst fracture typically has both axial load components as well as a flexion moment. Comminution is a function of the magnitude of force that was transmitted to the bone. It can be graded on the amount of the vertebral body that is involved and the amount of displacement. These grades have been used to understand the ability of that bone to support the anterior spine. Gaines described this load-sharing classification and the necessity for long-segment fixation or supplemental anterior support based on the concept of vertebral body comminution and fracture displacement.5 In healthy bone, this energy results in a burst pattern rather than a compression pattern. With failure of the anterior support, the spine falls into flexion with continued energy. The resultant disruption of the dorsal tension band or posterior bony fractures is usually the primary predictor of stability. Most classification systems recognize this, and posterior stability is a primary predictor of necessity of operative stabilization.6
Torsion
Complex fracture patterns often have a torsion component and can be responsible for fracture-dislocations with complete disruption of the anterior, middle, and posterior columns. Torsion injures are also common in the more flexible cervical spine. Typically, the failure is through the ligamentous structures because the oblique nature of the cervical facets allows for significant rotation. Torsional forces are the primary forces responsible for unilateral facet dislocations.7
Basic Anatomy of the Spine
These curves function to increase the flexibility and shock-absorbing capacity of the spine. The overall physiologic alignment must be maintained to prevent construct failure and accelerated degeneration. Sagittal balance is an indicator of physiologic alignment and is particularly important in lumbosacral procedures. In a normal spine, a plumb line called the sagittal vertical axis (SVA) can be dropped from the C7 vertebral body through the lumbosacral junction (Fig. 136-4). If the SVA is ventral to the lumbosacral junction, it is called positive sagittal balance; if the SVA is posterior to this junction, it is negative. Positive sagittal balance has significant implications for body mechanics and muscle work. Many authors describe a positive sagittal balance as an important factor in outcomes and muscle mechanics.8,9 To compensate, the pelvis shifts posteriorly and allows the patient to continue to maintain his or her global balance even with a positive SVA.10 The pelvis may also retrovert and move the center of gravity posterior to compensate for the positive SVA. Additionally, patients maximally extend their hips. Once this fails, they are forced to bend their knees and flex the hips in a biomechanically disadvantageous position.
Vertebral Body
The vertebral body is the bony cylinder that makes up the ventral aspect of each vertebra, except C1, which has no vertebral body. Each vertebral body consists of an outer rim of cortical bone surrounding a core of softer cancellous bone. The vertebral bodies resist much of the compressive loads placed on the spine in physiologic situations.
In general, the height, width, and depth of the vertebral bodies increase as the spine is descended, which seems to account for this increased strength at lower levels in the spine.1 As previously alluded to, there is a regional variation to the shape of the vertebral body. In the thoracic spine, the anterior border is shorter than the posterior border, creating a structural kyphosis in the thoracic spine. The outer shell of cortical bone is more rigid than the softer cancellous core because it is arranged in vertical lamellae to resist compressive forces. The cancellous bone is made up of trabeculae that are arranged to resist a variety of loads. There is greater compressive deformation of the cancellous bone prior to failure than of the cortical bone because of the increased rigidity of the latter.11,12 Numerous studies regarding the load-sharing properties of the cortical and cancellous bone have been performed showing that the load carried by the trabecular bone varies anywhere from 35% to 90%, depending on age and mineral content of the bone,13,14 and that the strength of the vertebral body decreases with age. Bell et al.15 have shown that there is a direct relationship between the mineral or ash content of the bone and the strength of the vertebral body. A 25% decrease in mineral content resulted in a greater than 50% decrease in vertebral strength due to loss of the trabecular columns that formed the core of the vertebral bodies. In osteoporosis, the mineral content of the bone is affected and results in loss of the horizontal trabeculae within the vertebral body core, thus lengthening the trabecular columns and compromising vertebral body strength.1 In the thoracic spine, the vertebral bodies articulate with the ribs. This articulation with the rib cage significantly augments the strength of the thoracic spine. This articulation with the rib cage and the sternum significantly augments the stiffness of the thoracic spine by as much as 110% in extension and 30% to 45% in the other planes of motion.
The vertebral end plates are formed from the concave, 1- to 2-mm thick cortical bone at the rostral and caudal surface of the vertebral body. These are fused to the cartilaginous end plates of the intervertebral disc by a calcified layer of tissue known as the lamina cribrosa, which permits osmotic diffusion of nutrients for the intervertebral disc. In 1957, Perry16 extensively studied failure of the end plates under compression and noted that one of three mechanisms of failure occurs, depending on the condition of the surrounding discs. Fractures occurred centrally or peripherally or encompassed the entire end plate. In specimens with nondegenerated discs, the fractures typically occurred centrally, and in specimens with degenerated discs, the fractures occurred peripherally. At high loads, the fractures encompassed the entire end plate regardless of degeneration. The strength of the end plate itself has been evaluated as well with regard to resistance to penetration by graft material (subsidence) or disc material (Schmorl node). Kumar et al.17 determined the greatest resistance to penetration to be within the first 4 mm of depth and the end plate to be strongest at the periphery closer to the cortical margin. In fact, the weakest portion of the vertebral end plate is at the center, where it is the thinnest. With a nondegenerated nucleus, axial compression creates a central increase in pressure and deflection of the end plate. This leads to increasing bending stresses in the center of the vertebral end plate and ultimately results in its failure.1 In contrast, in the degenerated disc, the nucleus lacks water content, and there is no build-up of central fluid pressure. The load is transmitted primarily through the anulus at the periphery of the disc and end plate, resulting in fracture in the same location or in the underlying vertebral body.1
Intervertebral Disc
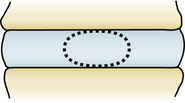
The vertebral bodies are separated at each level by the intervertebral disc. This viscoelastic structure is made up of a central nucleus pulposus, peripheral anulus fibrosus, and cartilaginous end plate of the disc, which separates it from the vertebral bodies above and below. Viscoelasticity is defined as a property of a material that exhibits both viscous and elastic characteristics when undergoing deformation. The material then has different mechanical properties that vary depending on the different loading rates. That is, if a load is applied slowly, the disc can respond with greater deformation, whereas if a load is applied rapidly, less deformation occurs. This property also changes as people age; with increasing age, there is a corresponding decrease in the ability of the disc to deform. There are 23 intervertebral discs starting between C2 and C3 and ending at L5 and S1. They make up 20% to 33% of the total height of the vertebral column, and there are regional differences that seem to parallel those of the vertebrae. The cross-sectional area of the discs increases in the rostrocaudal direction.
The central nucleus pulposus is composed of mucopolysaccharides and mucoprotein, forming a gel with water content ranging from 70% to 90%.1 The water content is highest at birth and decreases with age.18 The nucleus pulposus makes up approximately 30% to 50% of the cross-sectional area of the disc, and it seems to lie more posterior in the lumbar spine at the junction of the middle and posterior thirds of the disc in the sagittal plane.1 The viscoelastic properties of the nucleus pulposus allow it to act as an effective shock absorber for the spine. Surrounding the nucleus pulposus is the anulus fibrosus, which is made up of collagenous fibers in concentric laminated bands, with each band oriented 90 degrees to the adjacent bands and 30 degrees to the disc plane (Fig. 136-5). The inner fibers of the anulus are attached to the cartilaginous end plates, and the outermost fibers, known as Sharpey fibers, are attached to the cortical bone of the vertebral body. Because of the orientation of the fibers, the intervertebral disc effectively resists rotational, tensile, and shear stresses. The anulus does not resist compressive forces.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree