Basic Nerve Conduction Techniques

Robert J. Weber

Margaret Turk

Introduction

Nerve conduction studies (NCS) are the backbone of the electrodiagnostic evaluation. NCS are the most objective of the routine measures used in electrodiagnosis, and, not coincidentally, they produce the bulk of electrodiagnostic clinical fees. The accessibility of many peripheral nerves makes nerve conduction useful for survey approaches to peripheral nerve involvement in generalized diseases, for defining the nature of injury, and for the prognosis in focal peripheral nerve injuries. NCS are almost embarrassingly simple in concept: to determine the nerve conduction velocity (NCV) between two points along the nerve, record the amplitude of the response, and compare these values to the values of a normal population. But for the challenge of proper recording and interpretation, it would be duck soup! It’s worth noting that pioneer electrodiagnostic investigators would easily recognize current studies despite a half-century of rapid advances in medical technology. While much is similar, our understanding is far deeper and new challenges are always at hand. This chapter reviews the clinical challenges and physiologic principals of adult and pediatric NCVs. Understanding nerve structure and function at the molecular level is essential to incorporating the growing knowledge base of genetic and molecular-level pathology into daily electrodiagnostic practice.

Axolemma

Electrodiagnosis is the applied physiology of the peripheral nerve and muscle systems. Only neurons, muscle, and Schwann cells, plus several associated structures, directly participate in peripheral nerve conduction. These structures exhibit only a limited repertoire of electrodiagnostically detectable responses to injury. As if to emphasize the simplicity of the NCS, all of the signals used in clinical NCS are generated by only one structure, the cell membrane. Beneath this veneer of simplicity lies a billion years of evolutionary adaptation of the cellular structures that generate nerve signals. If our evolution began in a chemical soup of increasingly complex proteins and interdependent chemical cycles, then a necessary step to life is the packaging of this soup within a vessel that can carry it into less supportive environments. The cell membrane provides that function, and the self-assembly characteristic of its phospholipids is likely to have played a key evolutionary role in creating the living cell. While enclosure can create an autonomous cell, it also creates a need for the means to maintain a stable internal environment.

The cell membrane is composed of a 5-nm-thick, ordered, bilayer sheet of phospholipid molecules. Phospholipids are clothespin-shaped molecules with a charged, hydrophilic phosphorus-based head and two uncharged, hydrophobic, straight-chain hydrocarbon legs. If suspended in
water, these amphipathic molecules naturally form into capsule-like micelles with the water-loving, phosphoric heads outward facing, or they form into double sheets with each exterior surface composed of all phosphorus heads and an internal double layer of the water-avoiding hydrocarbon legs; thus, the interior of the membrane is highly hydrophobic. Such membranes are semipermeable. They exclude large molecules, water-soluble molecules, and all charged molecules (e.g., Na⁺, K⁺), while small, unpolarized, lipid-soluble molecules and some gases can diffuse through the membrane. The membrane interior is in fact a liquid, as described in the fluid mosaic membrane model of Singer and Nicholson (1), with the phospholipids able to move about easily within the membrane and the interspersed proteins able to migrate about, albeit more slowly. The phospholipid molecular structure and the type and volume of proteins seated in the membrane vary among different cell types. The fluidity of the membrane is affected by the inclusion of molecules such as cholesterol into the membrane, which stiffens in a warm membrane and increases the fluidity of a cold membrane, and by kinking of the hydrocarbon tail chains of the lipoproteins (double-bonding), which reduces the tight packing of the lipoprotein sheets by decreasing the Van der Waals bonding forces between the hydrocarbons and thus increases membrane fluidity.

Membrane Proteins

With cells enclosed by a barrier membrane that prevents simple diffusion of many essential substances such as charged ions, a transport mechanism across the membrane becomes essential for electrophysiology. This is achieved through the special association of adapted protein molecules with the membrane. While it has long been recognized that proteins are a major constituent of the membrane, their actual structure and functional organization have only recently been detailed. Membrane proteins can be described as extrinsic (peripheral)—that is, merely attached to the membrane surface—or as intrinsic (integral), those seated into and often completely spanning the membrane. Integral membrane proteins can insert into the membrane with their “waist” compatible with the hydrophobic, internal environment of the membrane and their terminal segments compatible with the hydrophilic intracellular and the extracellular environments into which they project. Those that function as passageways through the membrane are termed pores, channels, or pumps. These proteins are able to transport ions with or against a concentration gradient and be gated (switched on and off), and they are highly selective of the substances to be transported. Transport against an ionic gradient (active transport) requires added energy expenditure, while transport down a gradient (passive transport), here termed facilitated diffusion (facilitation refers to the channel function of opening a path through the membrane), uses the stored energy in the gradient itself. Gating (opening or closing a channel) can be triggered by many means: voltage changes, chemicals, Ca⁺⁺, and mechanical forces. The proteins essential to axon signal conduction are voltage gated and will be the focus of discussion; however, recall that the myoneural junction is chemically gated with neurotransmitters, while muscle is Ca⁺⁺ gated.

One of the core functions of membrane proteins is to maintain the intracellular concentration of Na⁺ below and K⁺ above that of the external environment. This condition is essential for life processes. Signal conduction along the axon uses a highly adapted exaggeration of this basic cell function that can produce episodic, very high ionic fluxes across the membrane. Since cell membranes are essentially impermeable to charged ions, this homeostasis is achieved through the active transport of Na⁺ and K⁺ cations across the cell membrane during the “charging” of the membrane potential and facilitated diffusion during depolarization. The membrane constrains protein anions from leaving the cell cytoplasm by providing an internal, positively charged component and prevents the passive diffusion of Na⁺, K⁺, or Ca⁺⁺ cations back across the membrane in response to their transmembrane concentration gradients once these gradients have been established by active transport of the ions. The concentration difference (i.e., gradient of each specific ion) across the cell membrane (inside versus outside the cell) creates an electrical potential at the cell membrane that can be summed for the membrane as a whole through application of the Nernst equation. For mammalian nerve cells, the sum typically is 70 mV,
with the external surface positive in respect to the interior. Thus, a static electrical potential exists at the membrane in its normal “charged,” homeostatic state. This potential can do work, including that of signal conduction.

The work required to transport ions across the membrane is reduced if the protein structure forms a physical void on the membrane, thus permitting ions to diffuse into the cavity and shorten the transport distance. Once an ion transport candidate enters the portal, protein pumps bind the ion to a specific site inside the protein and then must pass it stepwise through the membrane using a series of conformational changes and sequential binding sites along the path inside the protein. While this is cumbersome, it is well suited to propelling the ion against the gradient, with the added benefit that the passageway is firmly blocked by its conformation to prevent passive ion leakage or passage of competing ions. Channels, in contrast, enable the high ionic fluxes essential for creating a depolarization spike by offering a more straight-through path, with selectivity based on a close match between the physical characteristics of the ion and those of the channel, and employing a more limited, charge-based selectivity. These channels are voltage gated (i.e., opened by electrical field effects) to alter their conformation in order to permit a rapid flow of the selected ions through the pathway.

MacKinnon’s work demonstrated that selectivity of the K⁺ channel results from a filter effect that uses the significant difference in diameter of Na⁺ and K⁺ ions, and the geometry of their respective linkages to water in solution and to the dipolar oxygen atoms exposed in the internal protein channel pathway. The fit of K⁺ bound to water into the similarly scaled, charged environment of the protein path promotes the energy-free stripping away of the water and the subsequent progression of the K⁺ into and through the channel. This structure provides the model for high-flow, facilitated-diffusion–type ion channels that are necessary to produce the sharp, ion-generated voltage changes needed to open more membrane channels and propagate axon membrane depolarization. Actual conduction of electrical signals along the membrane is accomplished by sequential, voltage-dependent opening of sodium conductance channels along the axon membrane. Once triggered at any point on the axon, the signal propagates both centrifugally and centripetally along the full surface and length of the membrane (axolemma).

Resting Membrane Potential

The axolemma exhibits an electrical charge of -70 mV on its inside compared to its outside surface when in its resting (i.e., standby) state. This is due in part to passive and in part to active processes: membrane permeability, ion gradients, electrical gradients, and sodium pumps. The membrane structure absolutely prevents the movement of the negatively charged protein anions from the cell (some are physically anchored, and others are too large to squeeze through pores), creating a permanent, negative charge within the cell that attracts cations. While the membrane is effective in blocking ion passage, there are pores that permit some passive ion migration. This permeability is very much greater for K⁺ ions, the relationship being K⁺ >> Cl⁺ >> Na⁺. Since the K⁺ ion is the species most able to diffuse into the cell and its positive charge is electrically attracted to the negatively charged anions inside the cell, its concentration inside the cell increases. As the K⁺ ion concentration inside the cell increases, entry is progressively opposed by the increasing K⁺ osmotic gradient across the membrane until the electrical attraction of K⁺ into the cell equals the concentration gradient force to move it out. At that point a relative equilibrium for K⁺ is established. For K⁺ this occurs at a membrane voltage of -90 mV, and similarly the equilibrium is +60 mV for Na⁺ and -70 mV for Cl⁺. Other factors complicate the picture, such as increased K⁺ ion positivity inside the cell provides electrical attraction for Cl⁺ and simultaneously further impedes Na⁺ entry.

An entirely passive process cannot maintain the membrane charge, and the active work of maintaining the axon membrane potential is provided by the sodium-potassium-ATPase pump. This membrane protein internally binds three intracellular Na⁺ ions and a single adenosine triphosphate (ATP) molecule. Hydrolysis of the ATP to ADP energizes the change in the protein conformation, and the three Na⁺ ions are subsequently exposed to the extracellular environment and expelled. This external conformation of the protein then binds two extracellular K⁺ ions,
the ADP is released, and the protein reconfigures such that the K⁺ ions are exposed to the intracellular environment and released. This series of reactions by a single membrane protein very neatly addresses the active transport requirements for the two key cations involved in axon signal conduction.

Action Potential

The charged, resting membrane stores energy in the form of its voltage gradient as well as its Na⁺ and K⁺ concentration gradients across the membrane. These stored assets are converted into an active electrical field (the action potential) by a sudden influx of sodium ions through the membrane. The propagation of this local potential along the full length of the axon constitutes nerve conduction. Hodgkin and Huxley described the basic physiology of nerve conduction based on the squid giant axon in a series of papers in 1952. In the resting state, the negative internal membrane charge and the low intracellular Na⁺ concentration present a strong attraction for extracellular Na⁺ ions to enter the axon. However, the intact membrane precludes Na⁺ entry. Sodium conductance protein channels are present in the membrane but remain closed at rest. These channels are voltage gated, meaning that they open due to changes in their protein conformation caused by a sufficient local voltage change. In axons, the Na⁺ channels open if the membrane voltage moves to approximately -55 mV (changes by 15 mV) in response to an applied electrical field. Smaller stimulations are insufficient to open the channels since the resting membrane potential is stabilized by compensatory outflows of potassium. Thus, a sufficient stimulus must exceed the compensatory capacity of the K⁺ ion outflow current. A sufficient stimulus electrically charges the capacitance feature of the channel protein, which then conforms so that its principal extracellular gate is in the open position. Na⁺ rapidly flows through the membrane, and this ion flux creates an electrical field that can be recorded with proper instrumentation. This is the all-or-none aspect of nerve action first described by Cajal. The free flow of Na⁺ into the cell alters the membrane charge, creating a further positive change to +35 mV, a total increase of +105 mV. This large spike will be useful later as we review the propagation of the depolarization wave. If left to flow to equilibrium, the Nernst equation predicts an even higher membrane voltage, but two factors blunt this response. First, a second gated protein formation on the channel closes after about 1 ms and stops Na⁺ flow cold. This structure is not voltage sensitive but rather is a time-dependent reconformation of the protein. Second, there is a delayed, gated opening of potassium channels accelerating K⁺ efflux from the axon that offsets the positive Na⁺ spike. K⁺ efflux continues until the membrane charge actually falls below the resting value (hyperpolarization) before returning to baseline status.

Signal propagation transmits information by moving a coherent signal along the axon to the endplate or soma. This involves translation of the active area of the membrane steadily along the course of the axon. This is possible because the electrical field generated by the opening of local Na⁺ channels is sufficiently strong to open adjacent channels and thus propagate the signal in a stepwise manner along the membrane. You’ll recall that the local voltage changes at the membrane during the Na⁺ spike described previously were about 105 mV. This compares very favorably with the voltage change needed to open a Na⁺ channel of about 15 mV (the threshold voltage is -55 mV). Thus, local ion currents are able to flow along the axon, spreading from channel to adjacent channel once they are initiated. Normal conduction signals start at one end of the axon and propagate to the other, while those initiated at intermediate points propagate simultaneously in both proximal and distal directions.

This can raise the question of why a propagating wave front does not propagate back along the axon to form a reverberating circuit. This is prevented by absolute and relative refractory periods (i.e., a period of complete or reduced axon response to stimulation), which are present as the membrane recovers from an action potential Na⁺ spike. The absolute refractory period lasts about 1 ms, during which time there is no axon response regardless of how strong a stimulus is delivered. This occurs because:

Every Na⁺ channel in the area was opened during the initial (all-or-nothing) action potential.
Every Na⁺ channel is temporarily blocked from “recycling” to its ready state.
The second arm of the protein channel that reconformed and shut down Na⁺ flow (described above) still physically blocks the channel.
The second arm is not sensitive to voltage (remember that it switches based only on elapsed time).
The second arm is conformed to prevent the voltage-sensitive gate protein from returning to its ready position.

In this physiologic refractory state, no matter what the voltage change, no sodium channels are available to open. The relative refractory period begins when Na⁺ channels begin reconfiguring to their ready state. Reconfiguration occurs after different intervals in different channels. Both the opening and resetting of these channels are stochastic (i.e., it occurs randomly) once conditions are possible. What is seen is that progressively more Na⁺ channels are responsive to stimulation and the voltage change needed to trigger depolarization gradually returns to normal. Note that hyperpolarization of the membrane is not a factor in the absolute refractory period since it modulates only the voltage intensity required to stimulate, not the ability of the membrane to respond. The refractory period of an axon determines its maximum firing frequency by setting the minimum interval between conducted signals. This in turn sets the limit on the amount of information a single axon can deliver, since the axon’s all-or-nothing depolarization strategy keeps the amplitude of the discharge constant and frequency modulation (firing rate) is the only factor that can be varied for encoding information.

Conduction velocity is a critical factor in effective information transmission. The time required to deliver certain urgent signals can be critical to the survival of large, complex organisms. The simplest protective reflex response of the human foot travels a 2-m-long circuit. This signal must be transmitted along an extremely thin axon with a diameter of less than 20 μm, and so it has a length-to-diameter ratio of 50,000 to 1 or more. All of the axon’s structural components and energy sources are transported from the soma via a highly structured active transport system. The most rapid physical movement of moieties down the axon (rapid transport) requires many hours. With physical transport of information obviously far too slow, the rapid depolarization wave method of signaling is a necessity. Both the speed and the reliability of this signal are important and are insured through numerous cellular-level adaptations.

Each opened Na⁺ channel generates a finite flow of ions and thus a finite electrical field change. The effective force for opening a distant channel is the sum of the field forces generated by currently active channels. Because channel opening is stochastic, it requires a finite time for completion in any area, and so the electrical field generation is incremental. Electrical currents travel at the speed of light, so, practically speaking, they act instantaneously. Therefore, the speed of conduction along the axon can be explained in relation to characteristics of the channel protein and characteristics of the axon. The Na⁺ channel protein has capacitor-like characteristics in that it must be electrically charged before changing its conformation to open. This requires time and affects the conduction of current in the axon. An additional time increment is required for the protein to shift to its open configuration. Since there is a degree of randomness in the total time required to complete this transition, it contributes an irreducible component of the limit on conduction speed. The size of the axon strongly affects conduction velocity, with larger-diameter axons conducting faster. This relates to the decrease in electrical resistance through the cytoplasm with increasing axon cross-sectional area and is similar to the reduction in electrical resistance seen in larger-diameter wires. While the electrical current generated by the Na⁺ flow travels at the speed of light, the distance down the axon over which there is a sufficient stimulus to open (charge) channels is controlled by the axon characteristics. First, the axon has cable properties (an electrical insulator, the membrane, sandwiched between two conductors [the intracellular and extracellular fluids] makes up a capacitor) and the current in the axon must charge that capacitance, giving up energy that might otherwise open channels. Second, the channels themselves add more capacitance to the axon; thus, greater channel density on the membrane further slows conduction speed. All things being equal, larger axons have fewer channels per axon volume, lower cable capacitance and axonal resistance, and faster
conduction velocities. Since the channel opening speed is a constant between axons, conduction velocity in bare (nonmyelinated) axons increases by a factor of the square root of the diameter (√D). Thus, doubling the speed of conduction in unmyelinated axons requires increasing the diameter by four times.

All species scale up the diameter of axons to attain greater speed. The classic example of increased diameter in nonmyelinated axons is the giant axon of the squid. This axon functions in the animal’s propulsion system and is an essential component for escape from danger, and thus its conduction speed is vital. It is the largest known nonmyelinated axon, reaching 1 mm in diameter, roughly 50 times greater than the largest human axon. Its size has made it the preferred experimental model for nerve membrane since it permits easier intracellular instrumentation. Nonmyelinated axons in humans are typically less than 2 μm in diameter and conduct at a speed of a few meters per second (m/s). This is fast enough for autonomic regulation of internal body functions but far too slow for critical motor responses or complex cognitive functions. Axons in humans used for time-critical signaling can conduct at over 100 m/s. What are the prospects for scaling up the axon diameter like the squid to achieve this speed? The squid giant axon can conduct at 25 m/s, or one fourth of our 100 m/s target. Using the √D to reach this speed, the “human giant axon” could increase its velocity 4 times by increasing the diameter 16 times (i.e., reaching a 16-mm diameter). The cross-sectional area of this axon would be 200 mm⁺. Assuming that a typical peripheral nerve has 10,000 axons, a peripheral nerve of human giant axons could reach to 2 square meters in area (2,000,000 mm⁺)—not really a practical option!

Myelinated axons overcome this limitation by greatly extending the distance over which the propagating electrical wave front can open Na⁺ ion channels, thus enabling depolarization to leapfrog along the membrane in larger segments, a process known as salutatory conduction. This results from a beneficial association between the axon and a specialized neural support, the Schwann cell. Myelinated axon fibers are concentrically wrapped by the Schwann cell’s membrane. This divides the axon into electrically insulated segments, one segment per Schwann cell, with each segment stretching from 0.3 to 2 mm in length. The Schwann cell membrane has a high-lipid and low-protein content with little cytoplasm in the wrappings, making it an excellent insulator. Gaps between the segments, called nodes of Ranvier, contain essentially all of the conductance channels, creating a discrete electrical field generator. The internode segments covered by myelin have few protein channels and thus have reduced capacitance. This myelin cover improves the cable properties of the axon, reducing resistance and enabling the generators at the nodes to act at a greater distance. This moves the area of membrane depolarization two to three nodes along the nerve. This leapfrogging of the depolarization across nodes is saltatory conduction, and it greatly speeds conduction. Based on these changed axonal conditions, the conduction speed in myelinated axons increases in direct proportion to axon diameter rather than to the square root of the diameter, as seen in nonmyelinated axons. Myelination is critical for normal human nerve function, and both myelin pathology and the adaptive changes of the axon membrane in response to myelin play key roles in clinical disease and NCS.

Pathology

Myelinated axons demonstrate just three states of altered function: slowing of conduction, segmental conduction block, and loss of conduction along the full length of the axon. Myriad subtle modifications in the cellular chemistry and protein functions that accompany these changes lie beyond the reach of electrodiagnostic tests, in part obscured by the “all-or-none” character of axon function. The terms neurapraxia, neurotmesis, and axonotmesis appear frequently but offer more confusion than explanation. First, they indicate end effects rather than the underlying pathophysiology of nerve dysfunction. Second, they suggest a single status for the nerve when we usually deal with mixed pathology—fostering confusion between the status of individual axons and that of the total nerve. Finally, they are often simply misused. A more direct approach is to report a description of the nerve status using estimates of the
proportion of axons exhibiting diffuse slowing, focal slowing, focal block, or death.

Figure 3-1 • Demyelination pictured immediately following the onset of injury (A, A¹) and 6 weeks later (B, B¹) after myelin debris has been removed. The evoked responses with stimulation proximal (left) to and distal (right) to the lesion are demonstrated at A¹ and B¹ at the bottom. The demyelinated membrane (B) is able to restore some membrane proteins to restore propagation of the action potential, although at a slow velocity.

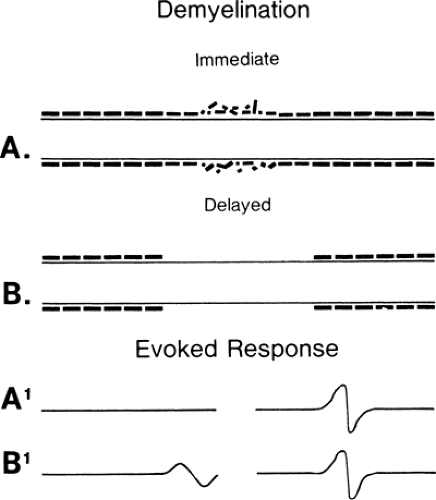
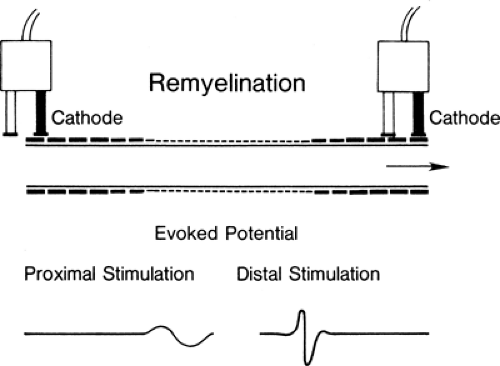
Conduction slowing occurs in three pathophysiologic conditions: demyelination, in which (after an interval) function resumes, as in an unmyelinated axon (Fig. 3-1) (see conduction block); remyelination, in which internodes are shorter because the new Schwann cell produces a shorter, thinner myelin cover; and reinnervation, where the axon diameter is smaller and Schwann cells also produce shorter segments (Fig. 3-2). In each of these cases, conduction time along an axon is increased because reorganization of the membrane proteins results in higher capacitance in the axon (see conduction velocity) due to the increased number of discrete depolarization points (channels) that must be charged. In practice, many variations on these extremes are possible: spotty demyelination, with demyelinated internode segments interspersed with normal ones; demyelination mixed with partial or light remyelinization; and partial remyelination mixed with normal segments. When myelin is absent along a long segment, the conduction velocity will be less than 20 m/s. Faster velocities suggest that demyelination is confined to a short segment that is “diluted out” by inclusion of a contiguous normal segment in the test segment, or that a mixed pathophysiology exists. When a segment is successfully remyelinated, the NCV often remains slightly slowed and may appear to be electrodiagnostically identical to large-fiber neuropathy. Compression neuropathies produce both demyelination and large axon loss. After surgical decompression both of these factors can result in residual slowed conduction despite “optimal” recovery. Distinguishing this optimal-but-slowed conduction state from a recurrent or persisting injury has become a cottage industry. In almost all instances this distinction is possible only with serial conduction studies that demonstrate change over time, or, in some instances, an unexpected failure to improve, or unusually good improvement following decompression.

Conduction block often occurs at a discrete location along the axon. Frequent causes include local stretch or compression, ischemia, trauma, or autoimmune or vascular disease. By definition, conduction block indicates an injury in which the axon survives (apraxia) despite the inability to
transmit a signal along a local segment. The segments of the axon above and below the block are normal and still conduct a signal when appropriately stimulated. Investigators have attributed conduction block to mechanical distortion of the axon (2) (Fig. 3-3) and to an impedance mismatch (3,4) at the junction of the myelinated and the demyelinated segment. The absence of cell membrane proteins on bare internode segments provides a convincing mechanism for conduction block in demyelination (5) since conduction through the demyelinated region would fail due to extinction of the Na⁺ depolarization current when the demyelinated region extends more than the two or three internodes across which the electrical field of the last intact node of Ranvier is able to produce an action potential. Thus, an axon exhibits conduction block once a multi-internode area is denuded. It can resume conducting only if additional membrane proteins are inserted into the membrane so that it can function in a nonmyelinated mode, or when it becomes remyelinated.

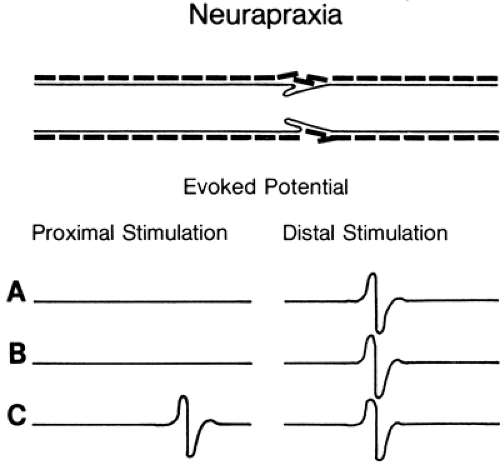Figure 3-2 • Remyelinated axon; note the decreased internodal distance and decreased thickness of myelin. The evoked potential with stimulation above and below the lesion that would be obtained from a nerve with all axons remyelinated is seen below. Conduction is slowed, and the response is temporally dispersed across the lesion.

Figure 3-3 • Evoked responses from stimulation proximal (left) and distal (right) to the lesion (A) immediately after injury, (B) 7 days after injury, and (C) some weeks following injury after neurapraxia has resolved. Compare to Figure 3-4.

Axon death results from a wide range of injury and disease. When the neuron cell body itself dies, there is no possibility of nerve regeneration. However, when only a portion of the axon has been disrupted, the surviving portion may die back to an intact node, stabilize, and attempt regeneration. Wallerian degeneration occurs in the axon segment distal to the point of axon disruption. Wallerian degeneration is the process of axon necrosis that dissolves and removes the disrupted neural segment and reorganizes the metabolism of any viable proximal segment. Axons are dependent on the neuron cell body to generate the energy and major subcellular structures needed for their function. These structures are transported down the axon as part of axoplasmic flow. Enough critical materials are present in the axon for it to continue functioning for several days independently. An axon cleanly separated from the rest of the neural cell will continue to conduct an action potential for 3 to 7 days (Figs. 3-4 and 3-5). During this period, responses of the separated distal axon segment to an adequate stimulation will remain essentially normal. This makes it impossible to distinguish
between a focal conduction block (neurapraxia) and the early stages of Wallerian degeneration. At the end of this 3- to 7-day period, axon conduction abruptly fails—that is, there is not a gradual decline but rather a precipitous one (recall the all-or-none rule). Once conduction fails, physical dissolution of the axon segment beyond the injury is rapid. The delay between injury and axon conduction failure means that electrodiagnostic distinction between conduction block and axon death can be made only at some point from 3 to 7 days after the injury (see Figs. 3-4 and 3-5). Nevertheless, electrodiagnostic studies should be performed as early after injury as possible to determine if some function is preserved and to obtain a baseline evoked response to compare with subsequent responses. It is very helpful to see the failure in conduction between two studies rather than simply not see a response in a traumatized limb! Electrodiagnosis can never determine if a nerve remains in structural continuity when there is complete loss of response to distal stimulation (Wallerian degeneration present), nor in cases of complete conduction block earlier than 7 days after injury (Wallerian degeneration not yet certain). Thus, the prognosis for axon regeneration that depends largely on the preservation of the nerve “skeleton” can be divined only by clinical judgment based on the mechanism of injury or by surgical exploration. By the same logic, the diagnosis of axonotmesis, which by definition is complete axonal degeneration with preservation of neural architecture such that regeneration can occur (6), cannot be distinguished electrodiagnostically from neurotmesis (loss of the neural skeleton).

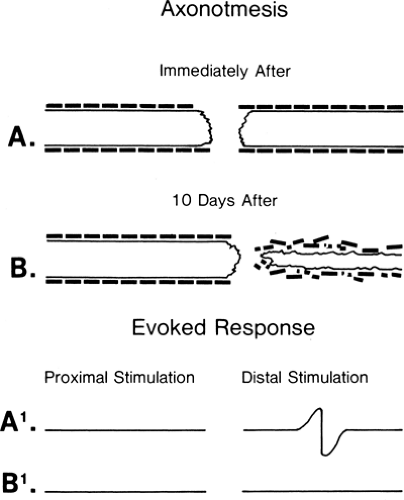Figure 3-4 • Axonotmetic lesion with axon changes demonstrated (A) immediately after injury and (B) 10 days after injury. The evoked responses obtained by stimulation proximal (left) and distal (right) to the lesion of the corresponding times (A¹ and B¹) are demonstrated at the bottom. In contrast to Figure 3-3B, the response is absent at 7 to 10 days.

Figure 3-5 • CMAP recorded from the thenar eminence with median nerve stimulation at the wrist in an individual with surgically demonstrated complete section of the median nerve following a stab wound in the upper arm. The top response was recorded 4 days after injury, the middle response 7 days after injury, and the bottom response 10 days after injury. (Sweep = 1 ms, gain = 1 mV.)

Up to this point we have worked with single nerve fibers, either nonmyelinated or myelinated axons. Single fibers generally exhibit a simple injury picture with only one pathophysiologic change, such as conduction slowing, conduction block, or axon death. In contrast, injured nerves in situ have thousands of individual axons and are capable of demonstrating combinations of these changes. Multiple abnormalities may be found within a short segment, at separate points along the nerve, or even at separate points on an individual axon. Interpretation of NCS can be complicated, and this highlights the importance of integrating the clinical and the electrodiagnostic examination when formulating the diagnosis.

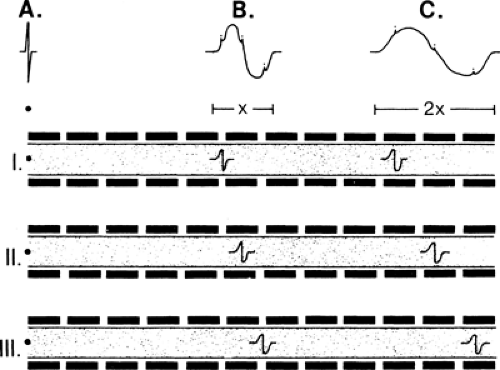
Evoked responses are signals produced by the artificial, simultaneous stimulation of the nerve’s axons, with electronic recording at a site somewhat distant from the stimulation. They represent the basic data of NCS. Stimulation of a motor nerve and recording the depolarization of a muscle it supplies produces a compound muscle action potential (CMAP) (Fig. 3-6). Similarly, stimulation of a sensory nerve and recording the signal of the nerve depolarization wave from a different point along the nerve produces a sensory nerve action potential (SNAP). Each of these signals has a distinct, consistent shape (Fig. 3-7) that, except for amplitude differences, varies little from nerve to nerve.

The recorded SNAP signal represents the summated action potentials (both negative and positive voltage components) from each of the nerve’s axons. The consistency of the shape comes from the consistent “normal” distribution of axon velocities in human nerves, which in turn creates a typical summation pattern. The summation of

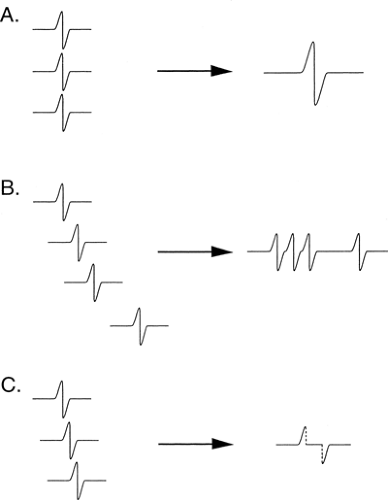
individual axon responses into an extended response is illustrated in Figure 3-8. If each axon conducted at the same velocity, then the duration of the summated evoked response would be the same as that of a single axon action potential, and the amplitude of negative and positive components would be in proportion to the number of axons (Fig. 3-9A). Conversely, if each axon conducted at very different velocities, the compound signal over a sufficiently long segment would be a sawtooth, with each deflection produced by one individual axon (see Fig. 3-9B). In the real world, axons exhibit a relatively narrow range of conduction velocities, and the pattern of velocity distribution is consistent among nerves. Although the signals do not arrive simultaneously from all of the axons, the variation of their arrival times is well grouped, and there is significant overlap of the axon signals. This spreading out of the evoked potential is called temporal dispersion. This staggered arrival of individual axon potentials at a recording electrode produces overlap of positive and negative components, resulting in cancellation of part of the signals, which is called phase cancellation (see Fig. 3-9C). Thus, a nerve with a normal complement of healthy fibers will produce a signal with normal temporal dispersion and typical phase cancellation, resulting in the standard shape. However, phase cancellation eliminates any simple correlation between signal amplitude (or area) and the number of axons contributing to the response.

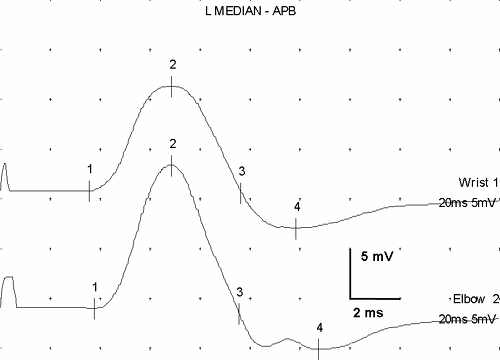
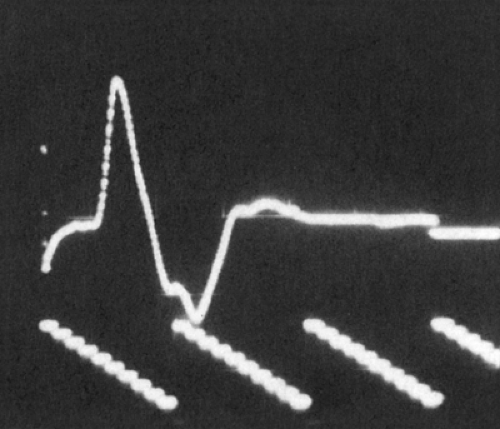Figure 3-6 • CMAP with recording electrode over the motor point of a single muscle. Note initial negative deflection (negative is upward in the figure).

Figure 3-7 • SNAPs recorded from three different nerves demonstrate similarity of shape despite anatomic and (mild) pathologic differences. Median nerve recorded from digit 3 after wrist stimulation (14 cm) shows mild delay (upper) compared to ulnar response from digit 5 at the same distance (middle), and this latency difference suggests mild entrapment. Lower trace is from a 10-cm segment of the lateral antebrachial cutaneous nerve. (Sweep = 1 ms, gain = 20 μV.)

Figure 3-8 • Temporal dispersion. Three axons of various conduction speeds, I (slowest) to III (fastest), are illustrated. The summated response of the signals from each of these axons is shown (A–C) at distances along the nerve. Conduction begins at the left and proceeds to the right. At point A, the signals in each axon arrive almost simultaneously, producing a very compact recorded response. At point B, the signals are less well synchronized, producing a smaller-amplitude and longer-duration response. This spreading is increased by the time the signals arrive at point C. The first potential to arrive establishes the take-off latency time, and delayed arrivals will increase the response’s duration. The greater the number of axons contributing to the signal, the smoother the curve of the recorded evoked response.

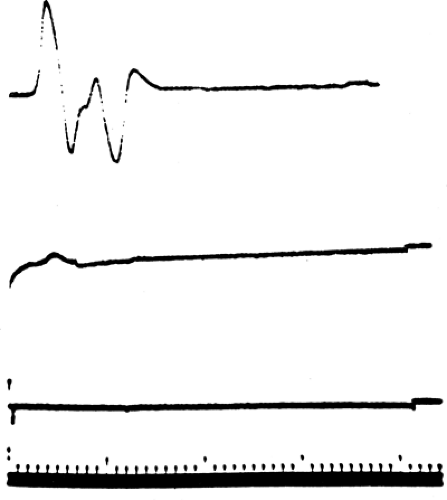
It follows that a different mix of individual fiber velocities would create a different normal evoked potential shape, which is precisely the situation seen in nerve pathology (Fig. 3-10). Computers enable us to mathematically model the way in which evoked potential shape varies with the distribution of individual fiber conduction velocities. These models demonstrate that up to 50% of the amplitude of the evoked potential of a typical nerve can be eliminated merely by altering the conduction velocity mix of its fibers. Thus, the recorded evoked response can be significantly reduced in nerve injury without any conduction block. This forces us to abandon the older concept in NCS that a “significant” (often 10% or 15%) drop in the size of the evoked potential across a point of injury indicates conduction block. Evoked potential decreases of at least 50% can be entirely due to the increased phase cancellation of increased temporal dispersion. In typical patients it is likely that a combination of conduction block and temporal dispersion will be in play, with each axon suffering a degree of myelin disruption and repair, or change in diameter. Needle electromyography can be helpful in separating blocked fibers from those that are slowed, since blocked axons cannot contribute to the voluntary recruitment pattern of motor unit potentials (MUP), whereas axons that are merely slowed will still activate MUPs and produce contractile force. Therefore, relatively good preservation of the recruitment pattern in the face of a major drop in the size of the evoked potential across the lesion indicates predominantly conduction slowing (phase cancellation) rather than conduction block, while a major-amplitude drop coupled with a greatly reduced interference pattern favors conduction block.

Temporal dispersion is an important, normal aspect of nerve conduction, and its exaggeration in
injury or disease is a key electrodiagnostic finding. This exaggeration cannot only reduce the amplitude of the response and prolong its duration, but also prolong its duration to such a degree that additional phases can appear in the response. Signals recorded directly from nerves (e.g., SNAPs) are briefer than the CMAP responses of motor conduction studies recorded over muscle because they contain only axon depolarization waves. The CMAP has a longer duration due to the longer time period of action potential propagation (slower conduction) of muscle membranes. Normal nerve evoked responses (SNAPs) are briefer than 2 ms, whereas motor responses (CMAPs) in hand and foot intrinsic muscles are less than 5 ms in duration (negative peak). Evoked responses longer than
these indicate increased temporal dispersion, either from disease or technical error (Fig. 3-11).

Figure 3-9 • Summation and phase cancellation. A. Simultaneous signal arrival (all axons at same conduction velocity) amplitude and area are a summation of the individual signals, while duration is the same as a single axon. B. No overlap (all axons have distinct velocities) leads to the greatest duration of signal, as the difference between the fastest and slowest axon is maximal. C. Phase cancellation due to overlap of negative and positive components of axons of slightly different velocities.

Figure 3-10 • Hypothenar muscle CMAPs from ulnar nerve stimulation at the wrist, below the elbow, and above the elbow. Note the loss of amplitude and area of the evoked response with conduction across the elbow, demonstrating mixed neurapraxia and conduction slowing with temporal dispersion. (Sweep = 10 ms, gain = 5 mV.)

Figure 3-11 • Median motor CMAP is recorded with E1 over motor point of the abductor pollicis brevis and stimulation 8 cm away at the wrist (upper trace). Excessive stimulation without movement of any electrodes activates the ulnar nerve (lower) by volume conduction. This adds the ulnar-innervated thenar muscles’ depolarizations to the recorded potential, creating an erroneously large and misshaped M-wave. (Sweep = 2 ms, gain = 5 mV.)

Where is the Lesion? Intraneural Anatomy

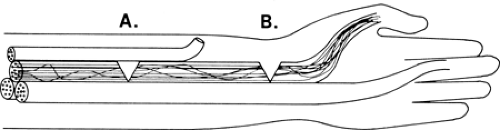
The interior architecture of nerves has evolved into a clever arrangement that protects against the catastrophic loss of whole functions from partial nerve injuries. The arrangement also turns out to be a key aid to the electromyographer’s ability to localize the point of injury along the course of the nerve. A typical telephone or fiberoptic cable has its individual fibers bundled into subclusters and the grouping remains unchanged throughout the length of the cable. All the telephone lines from “XYZ, Inc.” travel together in one of these small bundles and may take up the whole bundle. If someone cuts that bundle, “XYZ, Inc.” loses all of its telephones, but no other subscriber is affected. Similarly, neurons are grouped by function both in the brain and in the spinal cord, where focal lesions often cause discrete motor losses. If motor axons were grouped in nerves analogous to the arrangement in telephone cables, partial nerve injury might completely denervate one or two muscles while leaving others unaffected, even though their branches arise distal to the injury (Fig. 3-12). That arrangement also would make it difficult to locate the site of injury because there would be no difference in the observed effect of partial injury regardless of where it was located in the nerve.

Peripheral nerves, like cables, are also partitioned into bundles known as fascicles, and for much the same reason as cables: to provide better internal support and strength. However, unlike the wires in cables, the body employs a different
scheme of continually exchanging axons between the several fascicles within the nerve. This scheme continuously alters the axons that are traveling together and their location within the nerve as they move along its course (Fig. 3-13). With this arrangement, a partial nerve injury tends to spare some of the axons to each of the muscles supplied distal to the injury, since some fibers to each muscle are likely to be in spared fascicles, which results in partial function of most muscles. In addition, it is likely that each of the nerves supplied distal to the injury will have at least some abnormality, so that the distribution of abnormalities clearly locates the point of injury. Intraneural anatomy is thus the key to both reduce the functional impact of partial nerve injuries and also to better pinpoint the lesion.

Figure 3-12 • Hypothetical nerve in which all axons stay in a single fascicle until they exit the nerve. Note that a lesion at A or B would appear identical on needle EMG examination of both the distal muscle and the one innervated by the midforearm branch.

Reference Values

Nerve conduction reference values are established by performing a standardized testing method on a group of individuals that meet a pre-established set of qualifications. These usually include subjects who do not have neurologic complaints or disease; who are in appropriately good general health and without previous severe injuries or illness, environmental exposure, or special circumstances that would affect testing; and who collectively match the distribution of age, sex, and other features representative of the population to be tested. Notice that the group does not match the total population, but rather the population that is likely to be tested. If a clinical condition is found in a specific group, then normals should match that group if it has general characteristics that affect NCS values. Testing for chronic toxicity of an industrial solvent used for 50 years in a plant would require at least age-matching the subjects. “Normal” is usually defined statistically as the mean value plus or minus two standard deviations (SD). Although this approach is helpful, problems such as nonparametric distributions of population characteristics in the reference group can result in skewed statistics (as Mark Twain said, “There are statistics, damned statistics, and lies”). Examples of this type of characteristic are extreme limb length and height or extremes of age. Though not an indication of nerve pathology, groups with one of the characteristics would have mean nerve conduction values different from those of the total population.

Only gold members can continue reading. Log In or Register to continue