Fig. 1
Basic structure of the model. The model consists of multiple layers, of which the unit is given as spiking module (S-module) and oscillatory module (O-module). The unit receives inhibitory input from the units within the layer and excitatory input from the units in the neighbor layers
The S-module is described by a leaky integrate-and-fire model. It receives excitatory input from the S-modules in the neighboring layers, and from the global inhibition in the same layer. The S-module is also modulated by oscillatory activities of the O-module in the same unit. The activity of the i-th S-module in the k-th layer, v ik , is given by,
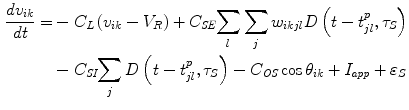 with
with
![$$ D\left({t}^{\prime },\tau \right)=\left\{\begin{array}{cc} 1 & \left(0\le {t}^{\prime}\le \tau \right) \\[4pt] {} 0 & \left(\mathrm{otherwise}\right) \end{array}\right. $$](/wp-content/uploads/2016/09/A315578_1_En_32_Chapter_Equb.gif) where D(t,τ) denotes a connection delay of a time constant τ, w ikjl denotes synaptic weight from the l-th unit in the j-th layer (1 represents the existence of connection and 0 represents no connection), t p denotes the time of the P-th spike, cosθ ik denotes the modulation from the O-module in the same unit, I app denotes the input current, ε s denote perturbation, and the capital letters are constants.
where D(t,τ) denotes a connection delay of a time constant τ, w ikjl denotes synaptic weight from the l-th unit in the j-th layer (1 represents the existence of connection and 0 represents no connection), t p denotes the time of the P-th spike, cosθ ik denotes the modulation from the O-module in the same unit, I app denotes the input current, ε s denote perturbation, and the capital letters are constants.
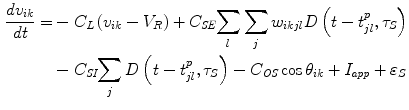
![$$ D\left({t}^{\prime },\tau \right)=\left\{\begin{array}{cc} 1 & \left(0\le {t}^{\prime}\le \tau \right) \\[4pt] {} 0 & \left(\mathrm{otherwise}\right) \end{array}\right. $$](/wp-content/uploads/2016/09/A315578_1_En_32_Chapter_Equb.gif)
The O-module models neural oscillations of EEG described by a phase oscillator [6]. In contrast to the neural mass model [5] in which variables are given by the sum excitatory and inhibitory activities in a local region, the phase model does not directly associate with physiological parameters, but it is nonetheless able to sufficiently describe the temporal dynamic of neural oscillator [7]. The O-module is activated by the S-module in the same unit and modulates its spike timing. The O-module also receives excitatory input from the O-modules in the neighboring layers and from the global inhibition within the same layer. The phase of the i-th O-module in the k-th layer, θ ik , is given by,
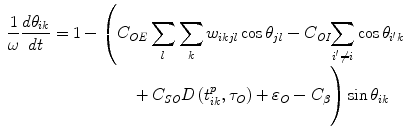 where ε O denotes perturbation, and capital letters are constants.
where ε O denotes perturbation, and capital letters are constants.
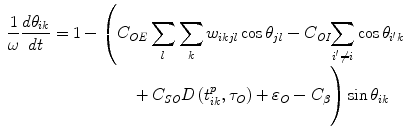
The spike transmission through multiple layers in the network is evaluated by the uniqueness of the activity propagation pathway organized in the network. To measure the uniqueness of the pathway, a pathway formation index, P, is defined as follows,
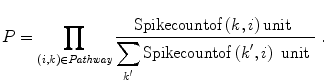 where P ranges from 0 to 1 and it becomes large in the case of a continuous pathway without branches and segmentation.
where P ranges from 0 to 1 and it becomes large in the case of a continuous pathway without branches and segmentation.
Parameters of the model are given as follows; C L = 50, V R = − 65, C SE = 4800, τ S = 0.01, C SI = 3000, C OS = 4000, ω = 10π, C OE = 0.15, C OI = 0.2, C SO = 1, C β = 1.2. These parameters were chosen to balance the excitatory input and the global inhibitions in each module. The frequencies of S- and O-modules’ activities are given around 40 and 10 Hz, respectively.
3 Results
The Units’ Activities in a Small Circuit
Figure 2a shows the temporal evolution of the S- and the O-modules’ activities in a single unit. The application of the input current to the S-unit resulted in the generation of spiking activity. This activity evoked neural oscillation in the O-module. Then, the spiking activity became bursting by receiving the modulation from the O-module. When the input current was turned off, both activities went back to resting states.
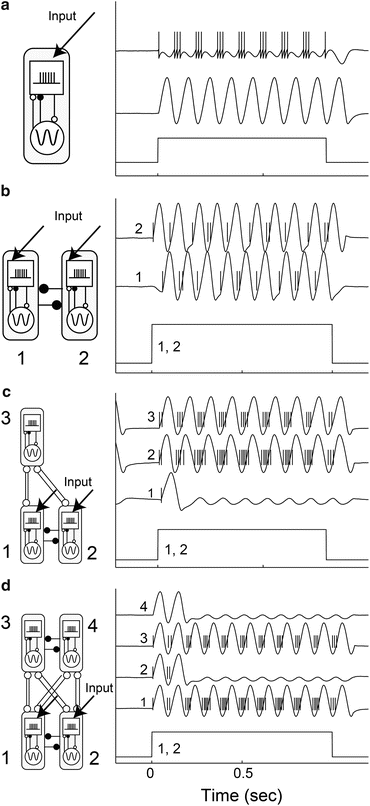

Fig. 2




Temporal evolution of each module’s activity in various small circuits. (a) A single unit, (b) a network of two units reciprocally inhibited, (c) a network of three units in which the two units are reciprocally inhibited and the other unit reciprocally activates both of them, and (d) a network of four units forming two layers. In (b)–(d), activities of S- and O-modules are shown in the same raw format
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree







