Considering Limb Impedance in the Design and Control of Prosthetic Devices

Fig. 3.1

Intrinsic stiffness of muscles and joints. (a) Short-range stiffness (SRS) for the plantaris muscle of the feline cat limb. Circles show experimental data from a single animal. Solid line shows short-range stiffness estimated from only the architectural parameters of the muscle. Similarity between experimental and modeled results illustrates how muscle short-range stiffness depends largely on muscle architecture (Adapted from [29]). (b) Stiffness for the human ankle joint during isometric dorsiflexion (triangles), plantarflexion (circles) and co-contraction with nearly zero net torque (squares). Figure illustrates how selective muscle co-contraction can be used to regulate joint stiffness independent from joint torque (Adapted with author permission from [58])

The impedance of a joint is determined by the inertial properties of the segments distal to that joint, and the viscoelastic properties of the passive tissues and the muscles acting across that joint. At a given joint angle, this impedance can be modulated through changes in muscle activation. The stiffness contributed by each muscle is scaled by the square of the muscle moment arm. There is also a kinematic stiffness proportional to the muscle force and the change in moment arm with joint angle [48]. Both of these factors emphasize the importance of geometry in determining limb stiffness [54, 53]. Due to the redundancies in the neuromuscular system, the stiffness of a joint can be modulated independently from the position and torque about that joint by selecting the muscles to be used for a given task and the relative activation of those muscles (Fig. 3.1b; [58]). These principles were a motivating factor in the development and use of impedance control in the field of robotics, and the recent application of these techniques to prosthetic control [1, 2].

Although assessments of muscle and joint impedance have contributed much to our understanding of the physiological mechanisms underlying stiffness regulation, few tasks are completed using individual muscles or joints. Rather, it is the coordinated activities of multiple muscles and joints that allow us to perform the vast repertoire of tasks we complete each day. For this reason, there has been much research into the regulation of multijoint impedance [19, 32, 39, 43, 77, 85], which is typically quantified by the endpoint impedance of a limb. Endpoint impedance describes the mechanical properties of a limb at the point of contact with the environment. As such, it is particularly relevant to understanding how we interact with our physical world and also for designing prosthetic devices the aid that ability. For most joints and limbs, impedance can be characterized well by a system having inertial, viscous and elastic (stiffness) properties [44, 58, 83]. To date that vast majority of studies considering endpoint impedance have focused on the arm, and many have only considered the stiffness component of impedance, thought to be most relevant for postural control (Fig. 3.2).

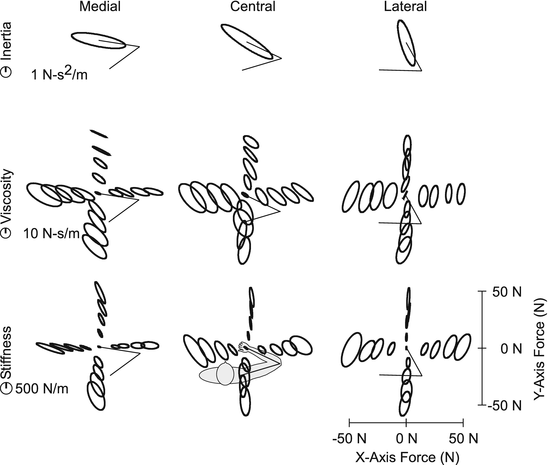
Fig. 3.2

Endpoint impedance of the human arm for different postures and endpoint forces. Three postures were tested, as indicated by the stick figure of the arm. Impedance was estimated for 17 different voluntary loads at each posture. The inertial, viscous and stiffness components of impedance are represented by an ellipse; the size of the ellipse represents the magnitude of the impedance component, and the orientation illustrates the direction in which each component most resists external perturbations of posture. Each ellipse is centered about a location corresponding to the average force exerted by the subject, except for the inertial ellipses which only changes with posture. These results indicate how both posture and muscle activation (i.e. voluntary force generation) influence the viscous and elastic components of endpoint impedance (Figure adapted from [83])

Hogan first proposed that the nervous system may explicitly control stiffness and that the redundancy of the human motor system may allow stiffness to be regulated independently from movements or forces required to complete a given task [49]. For a multi-joint system such as the human arm, impedance can be regulated not only by changes in volitional muscle activation described above, but also by changes in limb posture [38, 77]. Indeed, when subjects are free to choose between changes in muscle activation or changes in posture, they first choose to select postures that match the mechanical properties of the limb to the task being performed [118]. This approach likely reduces the effort required to complete the task, and may also increase performance through the reduction of motor noise associated with increased contraction [102]. The coupling between joints can be regulated by activating multi-joint muscles, which have an important role in transferring loads throughout the limb [130]. Selective activation of multi-joint muscles also provides a method for manipulating the spatial characteristics of endpoint stiffness (e.g. the direction of maximal stiffness and the relative stiffness in different directions), and maintaining stability [39, 44, 49, 72]. These important coupling issues have been considered for some time in the design of passive lower limb prostheses, but not upper limb prostheses. The advent of powered devices provides an opportunity to reconsider the potential benefits of inter-joint coupling and whether or not it might be beneficial to the use of upper limb prostheses.

3.2.2 Neural Feedback

There are numerous feedback mechanisms that can alter muscle activation and therefore change how the neuromuscular system responds to external perturbations of posture. These mechanisms thus influence the apparent mechanical properties of a muscle, joint or limb. Importantly, the behavior of many feedback mechanisms changes in a task-dependent manner [76, 90, 110], potentially providing insight to how the behavior of prosthetic devices might also be controlled to improve human performance in a wide range of tasks.

Rapid feedback mechanisms that occur prior to the onset of volitional activity are often described as reflexes or rapid motor responses. Those elicited by displacements of a muscle or limb are coined stretch reflexes. Houk was among the first to propose that spinally mediated stretch reflexes serve to regulate muscle stiffness [52]. Nichols and Houk [79] demonstrated this role in the cat soleus muscle, showing that stretch reflexes can compensate for nonlinearities, such as yielding, keeping stiffness relatively constant during stretch and release. Hoffer and Andreassen [47] extended these results throughout the physiological range of length and tension. They demonstrated that reflexes contribute to the stiffness of the muscle throughout this range and that they serve to keep stiffness nearly constant for muscle forces above approximately 25 % of maximum. Spinal stretch reflexes are similarly active for intact joints and limbs, and it has been suggested that they can contribute as much as 30–50 % of the net torque generated in response to postural perturbations [6, 21, 59, 84, 113]. The precise estimates depend on the joint being studied, as well as the techniques used to estimate reflex contributions to the net stiffness of a limb.

Reflex contributions to the mechanical properties of a limb can be varied in a task-dependent manner. Ludvig et al. [70] demonstrated that spinal reflex contributions to joint stiffness can be controlled independently from the intrinsic (e.g. short-range stiffness) contributions that vary with changes in steady state muscle activity. Longer latency stretch-evoked reflexes, including those mediated by supraspinal structures [22, 37, 81, 86], display even more task-dependence. One role particularly relevant to the regulation of impedance is that the sensitivity of longer latency stretch reflexes has been shown to increase to compensate for changes in the mechanical properties of the environment with which a limb is interacting. Specifically, reflex sensitivity increases during interactions with compliant environments relative to that observed during interactions with more rigid environments [4, 33, 34]. These results suggest that longer-latency stretch reflexes may serve to increase joint stiffness and stability during tasks in which that stability is not provided by the environment.

Stretch-evoked reflexes are also important for coordinating mechanical coupling throughout the limb. Many tasks, such as tool use, compromise arm stability along specific directions relative to the tool [93]. Stretch reflexes tuned to those directions could present an efficient mechanism for regulating arm impedance in a task appropriate manner. To be effective, such tuning would need to coordinate the activity of muscles throughout the limb so as to match the mechanical properties of the limb to those of the environment. Evidence for such adaptation and coordination was recently provided by examining how stretch reflexes throughout the arm adapt to environments that compromise limb stability along specific directions (Fig. 3.3; [62, 63]). A related role of long-latency reflexes is to compensate for the coupling torques between joints that arise during multi-joint movements [64].

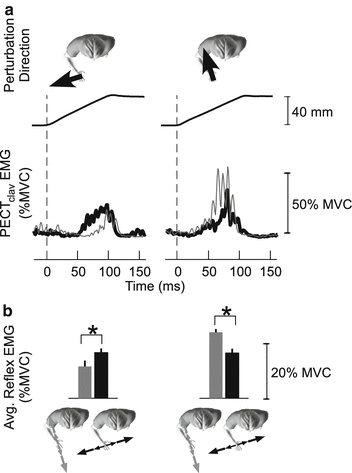
Fig. 3.3

Long-latency reflex adaptation in the human arm. Electromyogram (EMG) responses are from the clavicular head of the pectoralis muscle (PECT_clav) in response to ramp displacements applied to the hand. Displacements perturbations were applied as subjects interacted with unstable loads oriented along the hand-shoulder axis (gray lines and bars) or orthogonal to that direction (black lines and bars). Background muscle activation was constant for both loads. Results from one subject are shown in (a); group results from 5 subjects are in (b). Stretch reflex responses elicited by identical perturbations depended on the orientation of the unstable load illustrating how these feedback responses can compensate for changes in the mechanical properties with which a subjects interacts. Further details can be found in [63, 62]

Together, these findings highlight how the nervous system uses feedback to regulate limb mechanics and to adjust those mechanics in a task-relevant manner. These behaviors have already motivated some prosthetic designs [35] and may provide insight to how more complex behaviors, requiring the coordinated activity of multiple joints, may ultimately be implemented in a robotic device.

3.3 Estimating Impedance Relevant to Prosthetic Use

Whereas much has been learned about the regulation of human limb impedance, most studies have been performed under conditions relevant to only a limited repertoire of functions. These include tasks performed at a single posture and at fixed levels of muscle activation. These conditions allow for precise estimates of the limb mechanics, but it can be difficult to extend them to more dynamic conditions. Some elegant work toward this goal has been completed during upper limb movements [8, 19, 42], and for rapidly varying changes in muscle activation [71], though each of these studies still involved constraints not present during most natural tasks.

One of the most striking omissions in the literature is a lack of information regarding whole leg impedance during locomotion. This omission is due largely to the challenges associated estimating leg during all phases of the gait cycle. Experimental estimates of limb impedance require controlled perturbations to be applied to the limb, and the relevant forces and displacements to be measured [58]. These tasks are very difficult to achieve during gait, especially without disrupting natural gait patterns. Numerous studies have characterized the torque-angle curves during various locomotor tasks, but these cannot be used to estimate impedance [96]. Hence, the full information required to replicate the impedance of an intact leg in a prosthetic device is not yet available.

Two recent studies have made strides toward this goal by partially quantified leg impedance during locomotion. Each focused on the ankle. Rouse et al. [97] used a robotic platform to perturb the ankle during the stance phase, while Lee and Hogan [69] used a robotic exoskeleton to perturb the ankle during swing. Together, these studies provide the first glimpses into how ankle impedance is modulated throughout the locomotor cycle (Fig. 3.4). An interesting finding of each is that the estimated stiffness is low relative to that estimated when similar torques are produced during isometric conditions (for comparison see [55]). Furthermore, Rouse demonstrated that the estimates ankle stiffness was not significantly different than the slope of the torque-angle curve for this joint, which would not be expected a priori [96]. This empirical finding suggests that ankle stiffness during a large portion of stance phase can be approximated by a nonlinear spring, as described in more detail below. While the results shown in Fig. 3.4 were restricted to ankle motion in the sagittal plane, Lee et al. [67, 68] have also reported passive and active measures of ankle impedance in multiple degrees of freedom, including plantarflexion-dorsiflexion and inversion-eversion, which could ultimately be useful for generating more naturally compliant ankle motions in a prosthetic device.

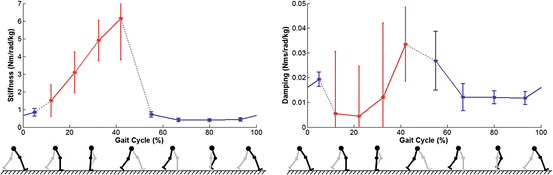
Fig. 3.4

Stiffness and damping properties of the human ankle during locomotion. The stance phase accounts for approximately 60 % of the gait cycle, beginning with heel-strike and ending with toe-off of the same foot, and the swing phase accounts for the remaining 40 % of the gait cycle. Ankle stiffness (left) and damping (right) values were normalized by bodyweight. Asterisks and error bars denote the mean and standard deviation, respectively. Red and blue colors denote results from Rouse et al. ([98]) and Lee and Hogan ([69]), respectively. No results were available for the regions indicated by the dashed gray lines. Note that the ankle stiffness showed an increasing trend throughout the stance phase until the contralateral leg hits the ground, and remained relatively constant during the swing phase. The damping also showed the similar trend as the stiffness, except for possible the drop in the early gait cycle

Due to the experimental challenges associated with estimating the impedance of the whole leg during locomotion [61], a number of alternative methods have been proposed. Pfeiffer et al. [87] developed an indirect method based on scalable models of muscle stiffness [29, 53]. This approach requires knowledge of only muscle activity, which is relatively easy to obtain, rather than the ability to perturb the limb throughout all phases of the locomotor cycle. This technique has been validated for the isometric conditions during which leg impedance can readily be measured experimentally, but stiffness estimates obtained during isometric conditions appear to be larger than those during dynamic conditions even for matched torque levels [69, 98]. Nevertheless, this modeling approach could be useful for providing an upper bound on the stiffness of the entire limb.

A very different strategy was recently developed by Aghasadeghi et al. [3], who used a parameter estimation algorithm to learn the impedance parameters of an equivalent leg controller that can replicate an observed locomotor trajectory. It is important to note that the goal of this work was to develop a controller that could replicate the kinematics of unimpaired gait (Fig. 3.5) without regard for how well these parameters matched the true impedance of the underlying system. The initial results of using this approach for prosthetic control are described below. They are promising, suggesting that it may not be necessary to precisely determine the mechanical properties of the intact limb as long as an equivalent controller can be obtained. To maintain perceptual and kinematic symmetry, however, it is likely that any equivalent controller will need to have mechanical properties reasonably similar to the intact limb. The exact degree of similarity remains to be determined.

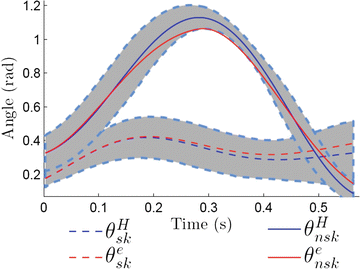
Fig. 3.5

Measured and modeled kinematics of the knee during the swing (θ _nsk) and stance (θ _sk) phases of locomotion. Superscript H corresponds to measured angles from a healthy subject walking at a self-selected pace. Superscript e corresponds to the angles obtained when simulating an equivalent impedance controller at the knee (Figure adapted from [3])

3.4 Mechanics of Traditional Prosthetic Limbs

The previous section discussed some of the physiological mechanisms contributing to the mechanical properties of human limbs, how those properties can be estimated, and how they are varied across tasks. While many of these issues remain active research areas, the importance of limb mechanics and the need to replicate some of their essential features in the design of prostheses has been appreciated for some time. This section provides an overview of some traditional approaches towards achieving this goal.

One critical feature influencing the performance of a prosthetic device is the mechanical interface that it presents between the user and the environment. This interface is affected by how the prosthesis is attached to the user, and by the mechanical design and control of the device itself. The net impedance of the prosthesis-user system is the serial connection of these two components. If there is a large discrepancy between the impedance of each component, the net impedance can be dominated by a single component. Although both the interface with the user and the design of the device are critical, few studies have considered each of these components in detail, even when the main objective has been to develop a system that presents an appropriate impedance to the environment. Therefore, a brief history of prosthetic design may be instructive for understanding how mechanical considerations have enhanced or limited prosthetic performance.

3.4.1 Mechanical Interfaces Between the User and Prosthesis

Almost all prostheses are attached via a socket covering the residual limb; much like a shoe covers a foot. These sockets are custom-made for each patient, usually by a certified clinician. A socket is normally placed over a substantial amount of soft tissue that surrounds a bone, except in the case of joint disarticulations. This soft tissue interface results in significant compliance that can limit the impedance between the user and the environment [132]. For a transhumeral prostheses, the rotational stiffness of this interface ranges from 40 to 120 Nm/rad [107]. Thus, it is not possible to create a trans-humeral prosthesis with a stiffness greater than this value when using a traditional socket. There are two promising alternatives to the socket interface. The first is osseointegration [15–17, 120], in which a steel connector is implanted into the residual bone. This connector protrudes from the bone through the skin, and is attached directly to the prosthesis providing a rigid interface from the prosthesis to the user. Invented in the 1990s, there are still concerns regarding deep infection of the bone [13], although progress continues to be made both in the implant design and in care of the insertion point. A more conservative interface is the SISA implant [100], a T-shaped device embedded in the distal end of the residual limb to replicate the function of the condyles present after a disarticulation. A less aggressive historical variant is the Marquardt osteotomy [80], in which the bone is broken and reset at 45° angle, or for lower-limb, the Ertl osseoperiosteal tibiofibular synostosis [57], in which a bone-bridge fuses the tibia and fibula together. With any of these approaches, the prosthesis can use these ‘condyles’ to achieve a more rigid connection, although one that is still substantially more compliant than the intact skeletal system.

3.4.2 Mechanical Design and Control of Prostheses

3.4.2.1 Upper Limb Prostheses

The mechanical designs for upper limb prostheses can be segregated in to four broad categories: (a) passive cosmetic devices, (b) activity-specific devices (e.g. a swimming paddle or screw-driver attachment), (c) body-powered devices, and (d) externally powered devices, of which the majority are myoelectric prostheses [126]. Here we will focus on the latter two categories for which general considerations of impedance control are most relevant.

In North America the majority of users prefer body-powered devices, due to the greater function they currently provide [114], their light weight and rugged design [41], and the simple manual control and associated proprioceptive feedback via extended physiological proprioception [112]. Though in common use, body-powered devices are often overlooked by researchers who tend to favor robotic prostheses, even though the performance of commercially available body powered devices has been estimated to exceed that of robotic devices by approximately 200 % [114]. Control of body-powered prostheses is commonly achieved through a Bowden cable that couples motion of an intact joint to movement of the terminal device. For example, using movements of the shoulders to control the grasp of a prosthetic arm. This direct coupling to the motions of the user allows for more accurate control of position and force [125], and more intuitive sensory feedback to the user [112] than can presently be obtained with myoelectric prostheses [74, 131]. Although there are many benefits, there are also limitations associated with body-powered devices. Most are associated with the limited motion of the intact joint used to control the device, especially since sufficient slack must be left in the cable to ensure that the prosthesis is not unintentionally activated when the intact joint is moved for purposes other than prosthetic control. For transhumeral prostheses, in which enough cable excursion must be available to operate both the terminal device (50 mm of excursion required) and the elbow (an additional 63 mm of excursion required), cable excursion is even a more limited resource [31, 40]. This limited excursion also restricts the options for implementing biomimetic impedance levels in a body-powered device because a compliant mechanism requires more cable excursion to achieve the same endpoint position than a rigid mechanism. This tradeoff has been seen most clearly by several groups designing body-powered continuously-variable transmissions (CVTs) [108, 123]. These devices operate similar to Robogrip™ pliers, in that they move quickly until an object is grasped. Further displacement shifts the gear ratio, such that user forces result in higher end-point forces. However, the excursion necessary to shift the gear ratio is often an expense prosthetic users are not willing to pay [123].

Myoelectric devices are becoming more common in North America, and many people alternate between body-powered and myoelectric prehensors, since almost all end-effectors are interchangeable. In Europe, the majority of upper limb prosthetic users with an active prehensor prefer myoelectric devices to body-powered devices [66]. This increasing use of myoelectric devices creates opportunities with respect to impedance control.

There are two important factors influencing the impedance that can be rendered by a myoelectric prosthesis. The first is the gear ratio between each actuator and the motion of the corresponding degrees-of-freedom. The intact musculoskeletal system employs strong actuators (muscles) with a limited range of excursions and speeds. Muscle actions are transmitted to appropriately scaled endpoint motions using bones as lever arms to amplify motions and scale down forces. In contrast to muscles, electric motors are generally weaker than required, thereby limiting size and weight, but have high speeds and an unlimited range of excursions. We accordingly use substantial transmissions to increase the force and decrease the speed into a functionally relevant range. These transmissions are often substantial (e.g., 600:1–1,500:1), and have two important effects. First, these high gear ratios improve the ability of the prosthesis to render positions, but drastically reduce the ability to render forces since the influence of the gear ratio has an opposite effect on these two quantities. Second, transmissions create amplify the motor impedance by the square of the gear ratio [26], making it difficult to obtain biomimetic impedance values. Of particular importance is the inertia of the rotor. Although some have advocated impedance-rendering control strategies [5, 45], the inertia of the rotor, amplified by the square of the gear ratio, tends to dominate the net impedance above moderate frequencies (e.g., 10 Hz) [107, 133].

The second factor limiting the impedance of myoelectric devices is that end-users often need to hold an object for extended periods of time. Weight is of paramount importance in prosthesis design [9–11], and even 50 g can result in the rejection of a device. Because electric motor-transmissions are inherently inefficient, particularly at stall-torque (0 % efficiency), current myoelectric prostheses use non-backdrivable 2-way clutches [28] to conserve power during periods in which it is necessary to forcefully grasp an object or maintain an arm against gravity for extended periods. It is possible but non-trivial to render impedances in light of these clutches [106].

3.4.2.2 Lower Limb Prostheses

For the reasons described above, both body-powered and myoelectric upper limb prosthesis have avoided compliance in their mechanisms. In contrast, impedance has been more widely considered in the design of lower limb prostheses, which are repeatedly used as a mechanical interface between the user and the ground. Many elegant mechanical designs have emerged over the last 500 years, with perhaps the most notable being the Anglesey leg, which used compliant cat-gut tendons to couple ankle and knee joints [14] as do the gastrocnemius muscles in an intact limb. A more recent incarnation of this leg is the hydraulically coupled Hydracadence 2 [99], which also couples the ankle and knee joints.

Prosthetic feet and ankles are a common place to incorporate mechanical compliance. Prosthetic feet serve four purposes: they absorb impact energy at the heel during initial contact; they store energy during mid-stance; they release energy during toe-off, and they provide stability during standing. SACH (solid ankle, cushioned heel) feet became popular in the 1950s due to the energy-absorbing properties of their cushioned heel, which serves as a damper. More recently dynamic feet with flexible carbon plates have become very popular; these can store up to 90 % of the energy placed into them during stance. Multi-axis feet add moderate compliance in other directions, including for torsional and side-to-side motions [57].

The mechanical properties of prosthetic knees have traditionally been designed to be dissipative, since the knee does not generate positive net power during level-ground walking [128]. Although simple friction joints work well at a single cadence, pneumatically or hydraulically regulated knees function better over a wide range of cadences, since the viscosity of their dissipative elements can be tuned appropriately [101]. More recent knees use microcontrollers to fine-tune dissipation over a range of speeds and activities [65]. Lower-limb prostheses that actively generate power have recently received renewed attention in light of improved actuator capabilities (e.g. [35, 46, 117]). Many of these legs actively exploit tunable impedance characteristics [82], some of which are highlighted below.

In summary, many prosthetic feet have substantial compliance, typically designed as an energy-storing element. In contrast, the majority of prosthetic knees have notable damping, either static or variable in nature.

3.5 Innovations in the Mechanical Design and Control of Prostheses

3.5.1 Mechanical Design

Continuously variable transmissions, which have not worked well for body-powered prostheses due to the excursion issues described above, have improved the performance of myoelectric prosthesis, where excursion is not a concern. For example, the Otto Bock Dynamic arm uses an elegant transmission in the elbow joint that couples with a cable, such that the arm reverts to zero impedance at full extension [91]. Zero impedance during full extension is important to facilitate a natural free-swing during walking, both to minimize energy consumption by the user and to facilitate a cosmetic appearance.

Series elastic actuators [88, 89] are a promising technology for regulating the impedance of a prosthetic device. The intentional introduction of compliance within an otherwise rigid electromechanical actuator has conventionally been avoided, because it reduces high-frequency performance and high-magnitude force generation; it also has the potential to introduce substantial dynamics between the sensors and actuators, which can limit the gains of a feedback controller. Nevertheless, for many applications these disadvantages are outweighed by the many advantages. These include: improved force rendering, improved force sensing fidelity [109], larger stable feedback gains when the sensors and actuators are collocated [127], and improved power densities that can be obtained by storing energy in the elastic transmission as is done in biological tendons [94]. This property of a series elastic actuator is often described as a catapult effect [5, 82]. Finally, series elastic actuators limit the maximum impedance at high frequencies [88, 89], which can be used to purposefully limit force levels, as an elastic transmission will reduce environmental contact forces transmitted through the actuator [5, 133]. For actuators with low endpoint inertia and viscosity, an elastic transmission also would limit the magnitude of the forces exerted on the environment. For these reasons, series elastic actuators are well suited to applications involving robot-human interaction. Accordingly, they been researched for application in rehabilitation devices including prosthetic ankles and elbows [7, 46, 105], rehabilitation robots for stroke therapy [115, 124], and other devices [119]. Active modulation of the impedance of these devices has been investigated for upper limb prostheses [12, 23, 36, 105], but has not yet been clinically implemented.

Only gold members can continue reading. Log In or Register to continue