Fig. 1
A unified view of motor control theories. Motor commands are generated according to an optimal feedback control policy, which embeds the requirements of the task. Body and environment react to these commands, and move to a different state. The sensory system measures the new state but, due to time delays in the neural pathways, it provides “out-of-date” measurements. Optimal feedback control, however, needs updated, rather than delayed, feedback information in order to generate optimal motor commands. Such an updated information is provided by a fast-state estimator, which integrates the sensory measurements (that possibly arrive from a variety of sensory streams) with a prediction of the sensory consequences of motor commands; hypothetically, this integration is performed according to the Bayessian framework. Predicted sensory consequences are generated by a forward model. This scheme has been adapted with permission from Shadmehr and Krakauer [104]
2.4 Equilibrium Point Hypothesis
An alternative to the models discussed so far is the so-called equilibrium point hypothesis (EPH) [32, 33]. This hypothesis assumes that the CNS controls body parameters rather than variables directly related to the task, and that movements emerge from the physical interaction between the appropriately tuned body dynamics and the environment. In particular, it is hypothesized that descending motor commands adjust parameters of the tonic stretch reflex in order to produce a desired equilibrium point of the limb [31]. Thus, the EPH exemplifies the main idea of the dynamical pattern theory of motor control, i.e., movements are emergent properties [102, 114].
To understand the EPH it is necessary to spend a few words on its key ingredient, the tonic stretch reflex. This is defined as a sustained muscle contraction in response to slow stretching [72]. When a muscle is slowly stretched by an external load, initially it produces an opposing force due to its passive elastic properties. If the muscle length overcomes a certain threshold, the subsequent activity of muscle spindles leads to the recruitment of a group of motor neurons, which causes the muscle to contract producing an active force that opposes the stretch. This force increases nonlinearly with the amount of stretch. For a given constant load, the muscle stabilizes at a given length called equilibrium point.
In the context of the EPH, the position of a limb results from the equilibrium points of the muscles around its joints. In order to generate voluntary movements, the brain sends descending commands that modify the threshold of the tonic stretch reflex arcs. As a result, new equilibrium positions are defined, and the limb moves accordingly. This idea has a few implications that are worth discussing. First, muscle activation is not directly controlled by descending motor commands, rather it results from the tonic stretch reflex. In other words, for a constant motor command (which defines the threshold of the reflex), different muscle activations as well as limb positions can be obtained depending on the external load. Second, there is no need to estimate the body state to compute appropriate motor commands. Indeed under an assumption of stability, the body will move toward the equilibrium point independently on its initial condition.
The problem of motor coordination is not solved by the EPH. A great number of variables, in this case the parameters of the stretch reflexes across muscles, should be coordinated in order to accomplish the desired task. How does the CNS solve such a redundancy? To this end, the uncontrolled manifold hypothesis (UMH) has been suggested as a general principle of coordination that could be applied at any level of details of the CNS. The idea is that the controller tries to keep the values of a group of task-related “elemental variables” (e.g., joint angles, muscles forces, muscle activations, thresholds of tonic stretch reflexes), named structural unit or synergy, within a subspace corresponding to successful task achievement (the uncontrolled manifold). Thus, the controller does not specify a single task solution (as in the case of optimal control), rather it facilitate variability within the uncontrolled manifold. In principle, this is the same behavior of an optimal feedback controller, which only reacts to deviations on task-related dimensions (see Sect. 2.2). The UMH and the notion of structural units have been used to explain postural control [42, 71, 74, 123] and manipulation [22, 73, 108, 127].
Usually, scientists who support the EPH are rather skeptical about the idea that the CNS learns and use internal models. Instead, they are more inclined to think that no heavy computations are performed, and that movements emerge from the interaction between body and environment. As a matter of fact, however, there is the need for the CNS to compute how to modify the parameters of the tonic stretch reflex in order to accomplish a desired task. Thus, a mapping between motor commands (i.e., reflex thresholds) and output variables (i.e., an internal model) might still be needed.
3 Motor Learning
Humans show a remarkable capacity to learn a variety of motor skills, whether it is adapting to changes in our environment, acquiring new skills, or improving existing skills. A lot of progress has been made on motor learning over the last few decades; however, researchers have a fair understanding of motor learning only of a narrow range of tasks, including simple reaching task in which different types of perturbations are applied. One of the exciting challenges ahead includes bridging the knowledge on simple movements to ‘real-world’ motor learning, and translating this knowledge to neurorehabilitation paradigms.
Motor learning is a broadly defined term referring to improvement in motor performance through practice [69]. It is believed that motor learning consists of multiple processes, of which motor adaptation and skill acquisition are considered to be the main processes in the literature [64, 69]. Motor adaptation is commonly defined as the response of the motor system to perturbations, such as changes in the environment, to regain a former level of performance in the new, changed environment [106]. Skill acquisition is considered to be a process in which task performance is improved beyond the baseline, mostly in the absence of perturbations. Researchers posit that skill acquisition is manifested by reduced motor variability and achieving higher levels of performance without a reduction of speed [69, 94, 109].
The goal of this section is to provide an overview on motor learning. Note that excellent reviews are already available describing the substantial progress of our understanding of the mechanisms of motor learning over the last decades (e.g., see Refs. [69, 106, 125]). Here, we give a short overview of the most important aspects of these mechanisms as a background for the other sections and chapters of this book.
3.1 Motor Adaptation
Motor adaptation has been investigated extensively using error-based learning paradigms, such as visuomotor rotations or force fields [105, 106]. In these paradigms, participants experience a perturbation resulting in a discrepancy between the predicted and executed hand trajectories; for instance, due to a perturbation in visual information (visuomotor rotations), or to perturbing forces (force field paradigms) [69, 106], see Fig. 2 for an short description of a visuomotor learning paradigm. Adaptation is the process that reduces the systematic error induced by the perturbation, and it is believed to occur through trial-by-trial adjustments of an internal model (the forward model) that maps motor commands onto predicted sensory outcomes. By doing so, error-based learning keeps movements well calibrated and correct for systematic biases [106].
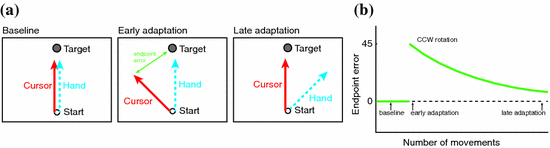

Fig. 2
A visuomotor rotation is a commonly used error-based learning paradigm. a Participants are asked to make movements with their hand so that a cursor moved from a starting position to a target. In the baseline condition, hand and cursor movement are congruent. In the adaptation phase, a visual rotation is imposed (45 degrees counterclockwise in this case) on the cursor movement; e.g., when moving the hand straight forward, the cursor would move at an angle. Studies have shown that participants gradually learn to move their hand in a way that compensates for the rotation, such that the cursor moves to the target again. b This figures shows a typical adaptation curve. When the rotation is introduced, the error at the end of the reaching movement initially is large, followed by a gradual decline of endpoint errors with increasing number of movements. At some point, the movement error is similar to the baseline, indicating that the participant is adapted to the visual rotation. Adapted from [82, 106]
3.1.1 Error as a Learning Signal
The learning signal driving adaptation in error-based learning is, as the name implies, the error signal between a desired and actual action, as well as the particular way the desired action was missed [106, 125]. The error signal is believed to adapt the motor commands, such that the error decreases in consecutive movements [106]. Wolpert and colleagues reported that in order to adapt to perturbations, the nervous system also estimates the gradient of the error with respect to each motor command component [125]. This means that the motor system needs to have an idea of how components of the motor command attribute to the error, and subsequently how the motor system can reduce the error. Wei and Körding posited that the sensorimotor system might adapt to errors in a nonlinear fashion [124]. They suggested that the sensorimotor system must weigh the information, in this case the error, provided by the uncertainty the information has in the signal. The ideal strategy, they argue, is therefore nonlinear, where small errors are compensated in a linear fashion and large errors would be disregarded. Errors that fall within the expected variance will be adapted for in a fairly linear way, whereas participants showed nonlinear and nonspecific adaptation to single trials containing error signals that exceeded expectation [41, 124].
3.1.2 Different Processes of Motor Adaptation
Temporal processes Smith and colleagues [111] proposed a model in which two parallel temporal processes drive motor adaptation: (1) a fast-acting process that learns and forgets quickly and (2) a slow-acting processes that learns and forgets more slowly. This model is able to explain complex features of motor learning such as spontaneous recovery of learning, savings (relearning of a perturbation or skill is faster than the initial learning), anterograde learning (the ability of a previously learned force field task to reduce the learning rate of a different subsequent task) and even patterns of 24-hour retention [61, 110]. More recent studies suggested that additional learning processes also need to be present to fully explain the temporal evolution of motor adaptation. Lee and Schweighofer [76] proposed a model with a single fast process combined with multiple slow processes, that could explain different types of adaptation tasks. An advantage of such a multi-rate learning model is that it can account for different temporal changes of the sensorimotor system, such as fatigue or injury [76, 125].
Model-based and model-free processes It is likely that multiple processes occur during motor learning, which are often classified as model-based learning processes (e.g., adaptation of the internal model) or model-free learning processes (e.g., use-dependent plasticity and reinforcement learning). For instance, studies have shown that several (model-free) processes occur besides error-based learning (adaptation): use-dependent plasticity [28, 56, 121] and reinforcement learning [56].
It has been shown that repeating a movement in a particular direction does not only reduce movement variability, but also creates a bias toward that direction in future movements [121]. This repetition-induced bias has been termed as use-dependent plasticity [69]. A couple of studies showed that when performing a reaching task in a perturbed environment, adaptation and use-dependent plasticity occur simultaneously [28, 56]. Huang and colleagues used a modified visuomotor rotation paradigm to show that participants, when adapting to the visuomotor rotation, create a bias toward the adapted movement direction [56].
In addition, Huang and colleagues [56] hypothesized that, during a visuomotor rotation adaptation task, hitting a target is a form of implicit reward driving a reinforcement process whereby successful error reduction is associated with the motor commands. They also showed that the model-free reinforcement learning process is independent of model-based learning (adaptation). Combining the model-based adaptation process with the reinforcement process leads to faster relearning (i.e., savings).
3.1.3 Structural Learning
Structural learning is a framework to explain the learning-to-learn phenomenom [14, 15]. Structural learning can be considered as learning certain features of a learning task, such that learning of similar tasks is facilitated. Braun and colleagues found support for structural learning by having participants perform reaching movements, during which random visuomotor rotations were imposed. The participants then adapted to a constant visuomotor rotation. They found that being exposed to the random visuomotor rotations facilitated learning in the constant rotation [14]. Braun et al. suggested that training with the random rotations allowed the participants to extract relevant features, or structures, of the task; all tasks were rotations. Structural learning is also consistent within the Bayesian framework, in that it would correspond to learning new prior distributions on the parameters of the perturbation [9, 10, 34].
3.1.4 Neural Correlates of Adaptation
Although the notions of different learning processes are intriguing, it is still not completely known how the brain performs all these hypothesized actions. Evidence suggests that the cerebellum plays an important role in trial-by-trial error-based learning [8, 26, 29, 117]. More specifically, some studies posit that the cerebellum computes the prediction error-driving adaptation [99, 113]. Patients with cerebellar lesions showed substantial impairment in fast adaptation across different tasks [26, 117]. Brain stimulation studies found that enhanced cerebral activity using transcranial direct current stimulation resulted in faster adaptation [44, 47, 100]. Where different types of adaptation are neurally stored remains an open question [125].
3.2 Skill Learning
Whereas in error-based learning, the motor system aims to reduce the error to zero, it does not systematically improve performance beyond baseline, a feature that is considered to be crucial in skill acquisition [82, 94, 109, 125]. Unlike adaptation, skill acquisition is studied for tasks where often no perturbation is present. Although different learning processes, such as reinforcement learning, are likely to play important roles in skill acquisition, they are not as well understood compared to the mechanisms underlying error-based learning.
3.2.1 Reinforcement Learning
To achieve an increase in performance, such as a reduction in error variability, reinforcement learning can help to find a solution to a movement problem. Reinforcement learning is driven by a reward signal; for instance, the information about the relative success and failure of a movement [41, 125]. In contrast to the error signal in error-based learning, a reward signal does not give information about the direction of required behavioral change [125]. Therefore, reinforcement learning tends to be slower than error-based adaptation. However, when a complex sequence of actions is necessary to achieve a goal, reinforcement learning can be used to explain what actions led to success and which led to failure, whereas error-based learning might be less successful.
3.2.2 Speed-Accuracy Trade-Off
Recent research has defined skill acquisition as a shift in the speed-accuracy trade-off function (SAF) [94, 109]. Reis and colleagues argue that defining skill acquisition as a shift in SAF is necessary, otherwise it is not clear how to relate changes in speed and accuracy to a change in skill. For instance, one could reduce execution speed and obtain a higher accuracy by “moving” along the same SAF, which would not reflect a change in skill.
Furthermore, Shmuelof et al. posit that a crucial concept regarding skilled performance is that successful execution and the trajectory kinematics associated with this execution are distinct. This is the case because only the task success is explicitly required, whereas there may be multiple kinematics that reach the desired goal [109]. In an experiment where subjects were instructed to follow a curved path without perturbation using wrist motions, the authors examined changes in the SAF and trajectory kinematics during learning. They found that practicing in restricted speeds led to a global shift of the SAF. Improved performance largely resulted from reduced trial-to-trial variability and increased movement smoothness. The authors propose that motor skill acquisition can be characterized as a slow reduction in movement variability, which is consistent with previous studies [85, 86] but distinct from faster model-based learning, which reduces error in adaptation paradigms.
3.2.3 Skill Learning and Optimality
Optimal feedback control (OFC), as described in Sect. 2.2, could be used to study skill learning [27, 69]. Although OFC has not been used to describe the learning process itself yet, it has been used to explain how we learn to control complex objects with internal degrees of freedom [87], see Fig. 3. For these tasks, there is no simple one-to-one mapping from the hand state to the state of the object (i.e., there are uncontrolled degrees of freedom). During training, participants interacted with the objects and showed improvements in meeting an accuracy criterion even though they had to move faster (i.e., shift in SAF, which is considered to be an improvement in skill). The hand kinematics after training could be described by OFC using a relatively simple cost function. The authors assumed that during training, the participants adapted to the complex dynamics in accordance with a model-based optimization of the cost function [87]. One could speculate that only the model-based optimization part would lead to skill acquisition; however, since the training was not the focus of Nagengast’s study, insufficient data were available. Krakauer and Mazzoni suggested that two processes could occur during training, leading to better performance: convergence to the optimal policy, or improved execution of the control itself. Either of these processes could lead to a shift in SAF [69] and to reductions in movement variability [85, 86].
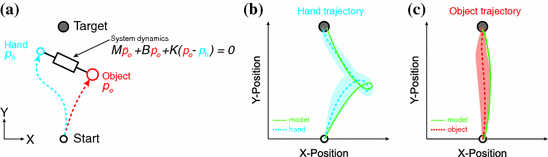

Fig. 3
Optimal feedback control could be used to study motor skill learning. as Schematic representation of the task. Participants were asked to move both their hand and and the object from a start position to a target within a prescribed time window. The hand and object were connected through the complex dynamics of a mass-damper-spring system. b The recorded hand trajectory (blue dashed line) and simulated hand trajectory (using OFC) are shown for a particular mass-damper-spring system. Note that a relatively complex hand trajectory was necessary to move the hand and object to the target. Nagengast et al. concluded that the simulated hand trajectory fits the measured hand trajectory well. c The measured object trajectory and simulated object trajectory describe a relatively straight line from the start to the target. As mentioned before, the simulated object trajectory described the measured object trajectory well. Adapted from [87]
4 Application to Upper Limb Prosthesis Users
“Neurorehabilitation is based on the assumption that motor learning principles can be applied to motor recovery after injury, and that training can lead to permanent improvements in motor function in patients with motor deficits”. Considering this statement of [63], the reconstruction of upper limb prosthesis user joint functions appears as a special case of neurorehabilitation.
Amputees have quite different medical history than, for example, stroke survivors. This is because prosthesis users have either lost one or more joints due to an accident, or they have already had received a surgery for reconstruction that unfortunately ended up in an amputation. Besides pain and physiological problems, prosthesis users become substantially influenced by psychological factors, such as (i) learning ability, (ii) cognitive skills, (iii) motor skills, and (iv) mental status (e.g., motivation, will, stress), which are situated in their mental–body. Thus, a prosthesis user needs time for adaptation and reorganization of the neuronal network to the new setup. It seems that they feel and imagine their original joints and they can also move them, a phenomenon called phantom limb [91], and that they can even feel phantom-limb pain [39, 101].
Reasons for amputation can be different; however, all amputees have to struggle with the new situation: some structure of their limbs is no longer present, but their synaptic input connections to the brain, say the neural network, is still present. Some afferent connections are lost, where the synapses are then somehow floating, say they are simply left open; and some efferent connections (i.e., axons from neurons that formerly have had controlled muscles of the lost joints) also end up. Patients have been able to perform mental finger motions right after amputation and after several years they are still capable of controlling their forearm muscles. This has been attributed as evidence to brain plasticity and reorganization [91].
Hence, exploiting the phantom-limb phenomenon could enable more intuitive prosthesis control to users. They may simply try to move the phantom-limb joints as if they used their original joints. In particular, contractions of residual muscles of the stump can be captured by means of surface EMG electrodes, and they can be used for the control of the prosthesis.
4.1 Prostheses of Today
Standard applications of prosthesis control use two EMG electrodes, one on the flexors’ side and one on the extensors’ side of the residual part of an amputated upper limb, either on the forearm or the upper-arm. Such a setup enables the control of at least one degree of freedom (DOF). In order to support more DOF, a switching mechanism is used to switch between available DOF. This switching mechanism can be implemented by co-contractions or other muscle activation sequences. Although this works in principle and it is relatively simple, the downside is that the full prosthesis control has a low chance to be integrated over time into dedicated motor programs by the user brain, because of the required switching actions.
In the last years, more dexterous prosthesis components and systems emerged on the market providing more DOF, e.g., the Michelangelo®-Hand Advanced Prosthesis System (Otto Bock Healthcare Products GmbH, D), the iLimb Hand (Touch Bionics, UK), the be-bionics-Hand (RSLSteeper, UK), or the Vincent Hand (Vincent Systems GmbH, D), to name a few. An EMG controlled prosthesis consists of an inner shaft and an outer shaft. The inner shaft carries the EMG-electrodes and fits the prosthesis user stump very tightly in order to provide a vacuum in the socket for fixation. The outer shaft is made of carbon or other material for protecting the prosthesis equipment and providing the carrier for the hand component. Fitting the prosthesis to its user is a mandatory step toward a successful prosthesis utilization.
For the control of advanced devices, more signals are required, and can be obtained using additional electrodes. However, muscles do not work independently, because of synergies that include groups of two or more muscles. Therefore, separability between single muscle contractions is not naturally given and can be achieved only approximately by intense training.
4.2 Prosthesis Control, Machine and Human Learning
It is assumed that a prosthesis user has at least residual understanding of doing phantom movements [91]. In addition, motor programs are assumed to work also for voluntary controlled joint movements [43] as they work for continuously repeated movements. The more degrees of freedom a multifunctional prosthesis provides, the more factors of user performance become important. These factors originate from users‘ motor abilities, such as the discriminability of their EMG signal pattern vectors between different phantom-like and the precision of repeating them always in the same manner.
During assessments, psychometric measures of user ability and classification performance for rating user performance in laboratory [45] and real-life scenarios [4] have been applied. When a novice prosthesis user tries to perform repetitions of the same movement, using a certain joint and using the same contraction, it can happen that the resulting outcomes are not always the same. This observation can be attributed to variability in motor control.
In order to face the variability of motor control, statistics and machine leraning are often used to control robotic prostheses. To this end, it is crucial that the collected training set provides sufficient information on the realtionship between EMG signals and desired movements. Figure 4 shows three exemplary training sets: (i) a small training set (pictured in red), which can be obtained with minimal training effort; (ii) a huge training set (black), which is robust to variability but it requires a very high training effort; and (iii) a medium training set (blue), which represents a trade-off between variability and learnability. In Fig. 4, a mean-shift1 between training and test data D is depicted. It is possible to notice that, while there is no overlapping between the small training set and the test set, the medium training set comprises the test set, thus it can lead to satisfactory performances.
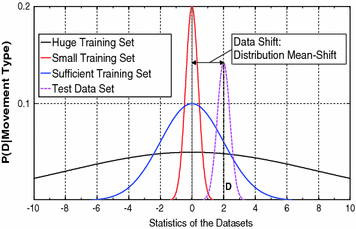

Fig. 4
Toy example of the statistics of three training sets with different data sizes and one test set D. The small set is out of only few training trials and a small mean-shift of the test set D distribution leads to nonfunctional behavior. The huge set is robust against mean-shift, but needs too much training effort. Thus, the sufficient set uses an optimized trial set and is more robust to slightly changed distributions
In conclusion, different phantom movements should result in differentiable muscle contractions with no overlapping EMG patterns. This can only be achieved by repeated training, perhaps with visual feedback to speed up the learning process.
4.3 Optimization of Training
Training amputees to use robotic prostheses should be divided in two components: (i) training for machine learning, which identifies a mapping between EMG readings and prosthesis joint control signals; and (ii) training for human learning, which should train amputees to perform stable and repeatable phantom movements..
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree





