Fig. 1
Phase lag values (vertical axis) in the neuropercolation model with excitatory-inhibitory layers; x-axis: time steps; y-axis: spatial steps (channels from 1 to 256). (a) Noise level 13 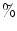 (subcritical): high synchrony is seen across the array; (b) Noise level 15
(subcritical): high synchrony is seen across the array; (b) Noise level 15 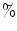 (critical): observe intermittent desynchronization across the array; (c) Noise level 16
(critical): observe intermittent desynchronization across the array; (c) Noise level 16 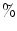 (supercritical): the synchrony between channels is diminished [9]
(supercritical): the synchrony between channels is diminished [9]
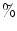 (subcritical): high synchrony is seen across the array; (b) Noise level 15
(subcritical): high synchrony is seen across the array; (b) Noise level 15 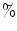 (critical): observe intermittent desynchronization across the array; (c) Noise level 16
(critical): observe intermittent desynchronization across the array; (c) Noise level 16 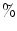 (supercritical): the synchrony between channels is diminished [9]
(supercritical): the synchrony between channels is diminished [9]Near critical state, we observe intermittent desynchronization over large cortical areas for a short period, see Fig. 1b. This is the period of phase transition, when large phase gradients travel rapidly across the cortex. This rapid propagation of phase synchronization-desynchronization resembles the rapid propagation of conscious broadcast as described by the Global Workspace Theory [1]. Recent ECoG experimental studies indicate that phase desynchronization and the collapse of analytic amplitudes are associated by the ‘aha’ effect of cognitive processing [11]. This leads us to the hypothesis that cortical singularities and phase dispersion could serve as neural correlates of the conscious broadcast.
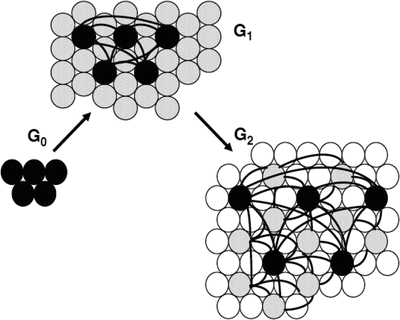
We have developed the Exponentially Expanding Graph model (EEGm) for brains based on planar geometric principles [4]. The development of brain structures can be described as the evolution that starts from an initial set of N pioneer neurons. N is typically a small number compared to the size of the fully developed brain. Pioneer neurons are modeled as small balls densely packed in a small area of characteristic size. During the developmental stage, this tiny cortical tissue with multiplies about 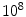 -fold, to have the fully developed brain with about
-fold, to have the fully developed brain with about 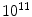 neurons. The evolution of the brain is described as the inflation of the initial graph
neurons. The evolution of the brain is described as the inflation of the initial graph 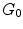 formed by the interconnected pioneer neurons, see Fig. 2. As the cortex develops, the space spanned by the neurons expands so that the distance between the original neurons increases. The space created by this expansion is filled with the newly created neurons. These new neurons grow connections to the existing ones. In the exponential model, an arriving new node makes connection to the existing neurons in its neighborhood within a disk D. A schematic view of the initial stage of development, from
formed by the interconnected pioneer neurons, see Fig. 2. As the cortex develops, the space spanned by the neurons expands so that the distance between the original neurons increases. The space created by this expansion is filled with the newly created neurons. These new neurons grow connections to the existing ones. In the exponential model, an arriving new node makes connection to the existing neurons in its neighborhood within a disk D. A schematic view of the initial stage of development, from 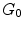 ,
, 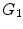 , to
, to 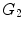 graphs is shown in Fig. 2. It is shown mathematically that the in-degree distribution approximately follows exponential distribution. The edge length distribution follows a power law. The exponent is 2, which equals to the dimension of the space in which the evolving neuronal population lives.
graphs is shown in Fig. 2. It is shown mathematically that the in-degree distribution approximately follows exponential distribution. The edge length distribution follows a power law. The exponent is 2, which equals to the dimension of the space in which the evolving neuronal population lives.
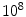 -fold, to have the fully developed brain with about
-fold, to have the fully developed brain with about 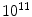 neurons. The evolution of the brain is described as the inflation of the initial graph
neurons. The evolution of the brain is described as the inflation of the initial graph 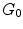 formed by the interconnected pioneer neurons, see Fig. 2. As the cortex develops, the space spanned by the neurons expands so that the distance between the original neurons increases. The space created by this expansion is filled with the newly created neurons. These new neurons grow connections to the existing ones. In the exponential model, an arriving new node makes connection to the existing neurons in its neighborhood within a disk D. A schematic view of the initial stage of development, from
formed by the interconnected pioneer neurons, see Fig. 2. As the cortex develops, the space spanned by the neurons expands so that the distance between the original neurons increases. The space created by this expansion is filled with the newly created neurons. These new neurons grow connections to the existing ones. In the exponential model, an arriving new node makes connection to the existing neurons in its neighborhood within a disk D. A schematic view of the initial stage of development, from 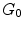 ,
, 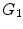 , to
, to 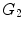 graphs is shown in Fig. 2. It is shown mathematically that the in-degree distribution approximately follows exponential distribution. The edge length distribution follows a power law. The exponent is 2, which equals to the dimension of the space in which the evolving neuronal population lives.
graphs is shown in Fig. 2. It is shown mathematically that the in-degree distribution approximately follows exponential distribution. The edge length distribution follows a power law. The exponent is 2, which equals to the dimension of the space in which the evolving neuronal population lives.
Fig. 2




Sequential evolution of the neuropil starting from a small set of pioneer neurons (black circles) 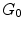 , through exponentially increasing neural populations of grey and white circles,
, through exponentially increasing neural populations of grey and white circles, 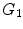 and
and 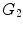 , respectively [4]
, respectively [4]
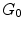 , through exponentially increasing neural populations of grey and white circles,
, through exponentially increasing neural populations of grey and white circles, 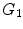 and
and 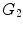 , respectively [4]
, respectively [4]Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree







