Field Dynamics and the Development of the Cerebral Cortex

Fig. 1

Left: idealized diagram of organization in V1 of OP, 0–180°, about singularities, and with marginal continuity, within an hexagonal framework composed of superficial patch connections. Right: experimental data [18]. The black areas are patchy synaptic connections

Hubel [4], in his Nobel address, hailed Mountcastle’s original proposal that columns formed fundamental building blocks of cortex as “Surely the most important contribution to understanding of cerebral cortex since Ramon y Cajal”. Enthusiasm for the explanatory power of the concept has since waned. Horton and Adams [5] described the cortical column as “a structure without a function”, and terminology describing them has become confused [6].

Difficulties arise partly because columnar structure is not clearly apparent outside V1 and S1, and because there is marked interspecies variation in definition of columns even in V1, to the point of apparent absence in small animals. Attempts to model the emergence of columnar organization of OP have also struck considerable difficulty. In some species there is clear emergence of structure ante-natally, rather than post-natally, yet models of the macrocolumn are generally dependent on response to visual features [7]. Which “features” are regarded as fundamental is also controversial, and how this relates to signal processing is problematic.

We have proposed a theory of emergence of cortical columns and their functional significance [8], which differs considerably from all other explanations. We base our explanation on two findings: (1) in vitro, embryonic neurons fire synchronously and self-organize into “small worlds” [9] and (2) synchronous firing of neurons prevents their apoptosis [10].

We assume synchrony and cell survival are causally linked – perhaps because some collective pumping action allows a synchronously coupled assembly of cells to increase their uptake of one or more vital metabolic substances. Therefore the emergent cell network would be that selection of cell types, and their arrangement, that maximizes the amplitude of synchrony for a given limit of total metabolic supply. The consequences of these assumptions are as follows.

2 Selection for “Small-World” Connectivity

Our arguments are based upon properties demonstrated in simulations of cortical gamma synchrony, and travelling waves [11, 12]. Closely situated cells are able to exchange synchronous pulses with smaller phase difference of afferent and efferent pulses. Therefore minimization of the total axonal lengths of their interconnections maximises synchrony magnitude (and uptake) while minimizing axonal metabolic cost.

In the dilute network of neuronal connections, the metric distance of soma separation is proportional to “degree of separation” in the topological sense. Therefore maximization of synchrony, by minimizing axonal lengths, selects a neural network with “ultra-small world” connectivity. This requires, in turn, that the average density of synaptic connectivity decline with distance as a power function [13].

A power function is the sum of exponential functions, and pre-synaptic densities of cortical neurons decline roughly exponentially with distance from the cell body [14]. Therefore small-world connectivity can be approximated from populations of neurons with differing characteristic ranges.

3 Local Variability of Axonal Ranges in the Selected Population

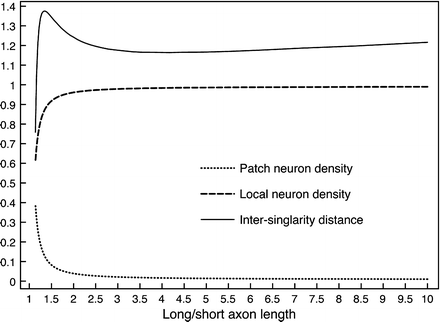
Equal approximations to a power function can be achieved by combining different relative densities of a variety of cell types, each type characterised by axonal length. Simplifying to only two types, Figures 2 and 3 show where long/short axon length is large (λ _β ≫ λ _α) approximation of a power curve requires the ratio of local neurons to patch neurons be large (N _β ≫ N _α).

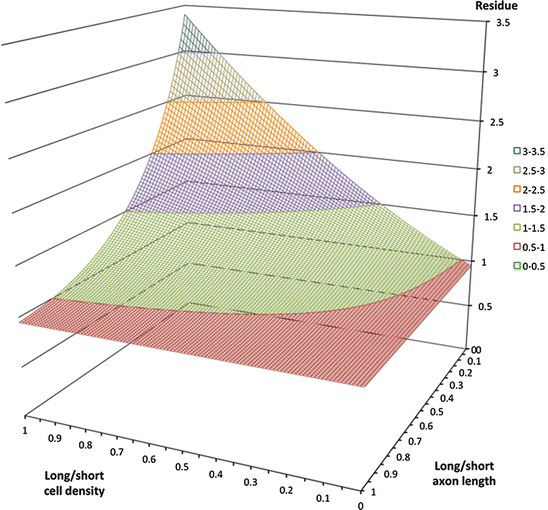
Fig. 2

Equal approximations to a power function can be achieved with a variety of combinations of cell densities and axonal ranges. Colour margins show fit-residual isocontours

Fig. 3

Cell densities and axonal ranges of local and patch neurons vary approximately inversely for equivalent fits to a power function obtained along the lowest-residual iso-contour in Fig. 2. Intersingularity distance (cp Fig. 4) is comparatively invariant over this range

4 Resolution into Macrocolumns

It can be shown that, where J is the magnitude of synchronous oscillation, and q,r are positions of excitatory neurons in the cortex,

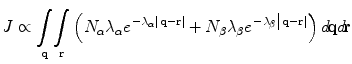$J\propto \underset{\mathbf{q}}{\int}\underset{\mathbf{r}}{\int}\left({N}_\alpha{\lambda}_{\alpha }{e}^{\left.-{\lambda}_{\alpha}\right|\left.\mathbf{q}-\mathbf{r}\right|}+{N}_{\beta }{\lambda}_{\beta }{e}^{\left.-{\lambda}_{\beta}\right|\left.\mathbf{q}-\mathbf{r}\right|}\right)d\!\mathbf{q}d\!\mathbf{r}$

Therefore synchrony is maximized by selection of that ensemble of cells in which the cells with relatively short but dense axons are closely situated to each other. Such packing forces the cells with long-range axons to form connections at longer range, enforcing a “patchy” connection system. Arrangement in an hexagonal patchwork optimizes this synchrony-facilitating orderliness, but a clearly demarcated arrangement of this type is only possible where

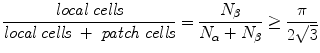$\frac{\textit{local}\; \textit{cells}}{\textit{local}\; \textit{cells}\; +\; \textit{patch}\; \textit{cells}}=\frac{N_{\beta }}{N_{\alpha }+{N}_{\beta }}\ge \frac{\pi }{2\sqrt{3}}$

This follows simply from the ratio of area of a circle to a hexagon, when local cells are enclosed within an hexagonal patch-connection frame. Therefore the absence of a clearly columnar arrangement does not imply a loss of the small world organization, nor does it deny that both short-range local connections, and longer-range functional connections are present – the distinct types are merely more entangled with each other (See Fig. 4).

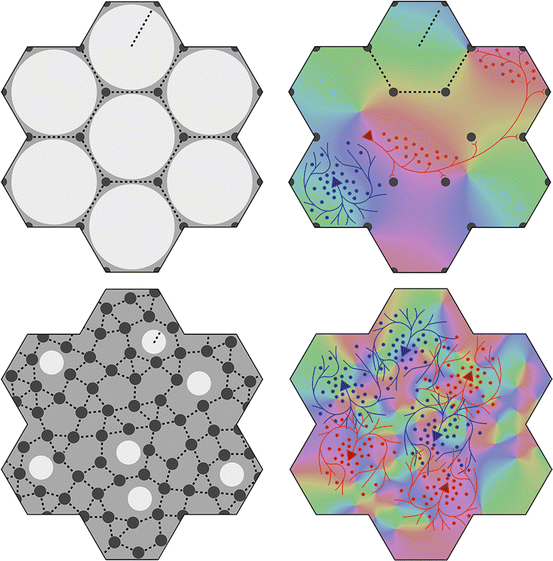
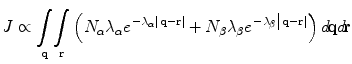
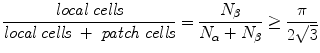
Fig. 4

Variation of the structure of macrocolumns at extremes of the axonal lengths and cell numbers in Fig. 3. Top: With large long/short axon length ratio, clearly resolved hexagonal organization emerges, with long (red) patch connections linking “like to like”, and highly clustered short intracortical axons (blue). Bottom: near-complete loss of resolution when long/short axon ratio approaches 1

Thus, variation of the clarity of demarcation of columns in differing cortical areas, and between species, need not reflect major differences in function.

5 A Mobius Map Within Macrocolumns

Restated in physical terms, the maximization of J requires the populations of cells of differing axonal range be geometrically arranged so as to permit maximum resonance throughout the system. Since the amplitude of synchronous oscillation declines with distance of separation of cell bodies, then the system of patch connections and the local neurons within each macrocolumn must achieve a 1:1 connection system, promoting resonance between cells in each macrocolumn, and the surrounding patch system, and thus forming an input map of the cortical surround, projected onto each macrocolumn. If it is additionally assumed that the competition for crucial resources is not simply between individual neurons, but also between closely situated pre-synapses arising from the same cell, then “winner take all” competition between closely situated synaptic connections would develop, and at equilibrium each cell would then require high firing correlation with some of its neighbors, and low firing correlation with other neighbors – and be correspondingly strongly linked to some neighbors by “saturated” synapses, and weakly to others by “sensitive” synapses. This intra-cellular constraint, along with the requirement to form a 1:1 map of connections between each macrocolumn and its patchy-connection surround, can be met if the connections within the macrocolumn form a closed system analogous to a Mobius strip. Figure 5 (left) shows how a dynamic equilibrium of synaptic connections can thus be struck. The mapping of the patch system onto the macrocolumn can be expressed as

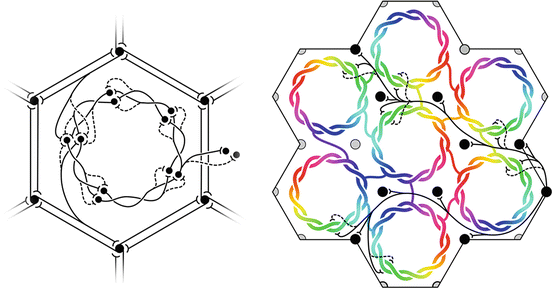
Fig. 5

Maximization of synchrony with local synaptic competition leads to Mobius ordering, within macrocolumns. Left: Equilibrium disposition of saturated (solid) and sensitive (dashed) synapses in the developing neocortex. Right: “Like to like” saturated patchy connections map the same part of the surrounding cortical field onto homologous cell positions on the Möbius configuration

Only gold members can continue reading. Log In or Register to continue