(1)
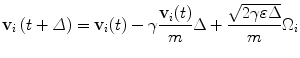
(2)
m, the molecular mass; γ, a friction term, which depends on the absolute temperature: γ = kB · T/D, where kB is the Boltzmann constant, T is the absolute temperature in Kelvin degrees, and D is the diffusion coefficient of Glutamate; ε = kB · T.
Concerning the GLUT/AMPAR binding we note that the results in experimental literature were obtained by imposing unrealistic conditions: stationarity of the Glutamate concentration within the synaptic cleft and a long period, of the order of milliseconds, for the exposition of receptors to Glutamate [2]. Conversely, when the neurotransmitters are released by a docked vesicle, the flow of neurotransmitters within the cleft is much faster and far from stationarity. In the lack of correct experimental data for the binding rates, we attempted a computation of the binding by using probabilistic arguments. We searched the unknown value of the binding probability on the base of a geometrical reasoning and through comparisons of the peak amplitudes between the computer simulated and the experimentally recorded mEPSCs. The main hypothesis is based on the experimental observation that the binding takes place when the GLUT presents a particular arrangement with respect to the binding site: the γ-carboxyl group of GLUT is in front [1]. To compute the binding probability we assumed an elongated shape for GLUT and we made the hypothesis that GLUT binds to the site only when the directions of the long axis belong to a restricted range of values. By considering a GLUT as a spindle set at center of a unit sphere, we hypothesized that only the directions contained within a (unknown) spherical cone, could produce the binding. Thus, the binding probability was computed as the ratio between the volume of the spherical cone and that of the unit sphere and, by varying the angle of the cone, we observed the effect of different binding probabilities on the synaptic response. In all our simulations only the AMPARs contributions have been considered for the computation of the mEPSC, since under normal conditions the ionic channels of NMDARs cannot convey currents. Thus, NMDARs were considered only as competitors of AMPARs for GLUTs binding.
The discretized Langevin equations were implemented in a parallel FORTRAN program by using MPI (message passing interface) routines. The paths of all the GLUTs were computed up to the occurrence of one of the following events: a re-uptake, a receptor binding or the spillover. The program was run on a computer based on a cluster of workstations. Single and double binding times between GLUTs and AMPARs/NMDARs were recorded in two matrices and used for the subsequent computation of the mEPSC by a program which produced the random transitions to/from open and close states and to the single binding states.
3 Simulation and Results
The new computer simulations investigated more thoroughly the phenomenon of the dispersion of the synaptic response. We analyzed the results obtained with three values for the binding probability, BP: 0.00496, 0.00874, 0.01360 (related to Spherical Segment Angle: 18°, 24°, 30°, respectively), and, for each probability value, two values for the number of AMPARs, one normal and the other very high: (A) 55 and (B) 154. (The respective values for NMDARs were 13 and 18.) For each couple (BP, AMPARs Number), six simulations with different GNR seeds were accomplished, for a total of 36 computer simulations. In all these simulations the vesicle was located at X0 = 0 and released 775 GLUTs. The total height of AMPARs (and NMDARs) was 17 nm, while the height of the portion of receptor protruding in the synaptic cleft was 6 nm. The relevant statistical values of the amplitude peaks of the computed mEPSCs are reported in Table 1.
Table 1




The first column, Case- with Low and High, is related to the number of AMPARs
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree







