(1)
where
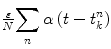 is the input to the jth neuronal oscillator from the kth neuronal oscillator, ε is weak coupling constant, N is the total number of neuronal oscillators, t n k is the nth firing time of the kth neuronal oscillator, α(t) is a causal coupling function. θ j is the phase of jth neuronal oscillator, ω is the natural frequency of a neuronal oscillator, Z(θ) is a phase response curve of a neuronal oscillator, c sin(ω 0 t) is an external periodic force with a strength c and frequency ω 0.
is the input to the jth neuronal oscillator from the kth neuronal oscillator, ε is weak coupling constant, N is the total number of neuronal oscillators, t n k is the nth firing time of the kth neuronal oscillator, α(t) is a causal coupling function. θ j is the phase of jth neuronal oscillator, ω is the natural frequency of a neuronal oscillator, Z(θ) is a phase response curve of a neuronal oscillator, c sin(ω 0 t) is an external periodic force with a strength c and frequency ω 0.We assume that the mutual interaction shift the frequency of the mean phase of these oscillators by εΩ from the natural frequency ω, and define the relative phase ψ j = θ j − (ω + εΩ)t. The relative phase ψ j changes slowly compared with and will hardly change during the oscillation period θ j . Therefore, we substituteψ j into Eq.(1), and average Eq. (1) over one period keeping ψ j constant, so the relative phase ψ j obeys the following equation:
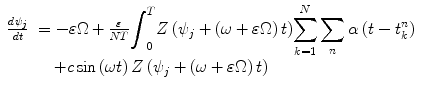
In order to investigate the dynamic response of neural population, we introduce complex order parameters describing synchronized phenomenon in the neuronal population
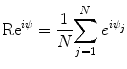
where R is the amplitude of the order parameters describing the degree of synchronization of neuronal oscillators, 0 ≤ R ≤ 1, the bigger R show that synchronous activity is stronger, ψ is the average phase of the neuronal population.
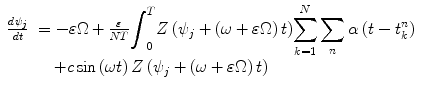
(2)
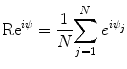
(3)
3 Result
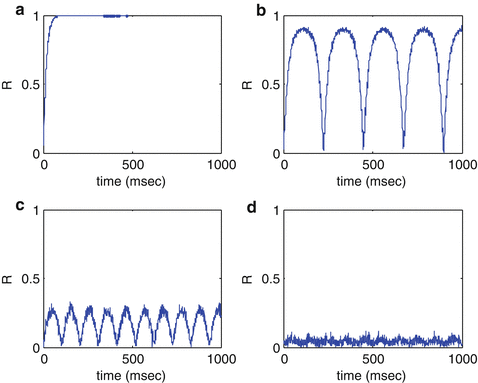
We investigate the response property of neuronal population to external periodic stimulus. The phase sensitivity function Z(θ) is considered as a sinusoidal sensitivity function sin(θ) as in Ref. [15]. As synaptic time constant τ is smaller, the neuronal population quickly synchronized in-phase (Fig. 1a); but with τ increased, periodic synchronization occurred, and as the synaptic time constant is larger, the synchronization become weaker (Fig. 1b, c); even more, synchronized activity can be lost (Fig. 1d). This shows that synaptic time constant is an important condition under which the global neural network synchronized.