Inspired Models of Decision Making

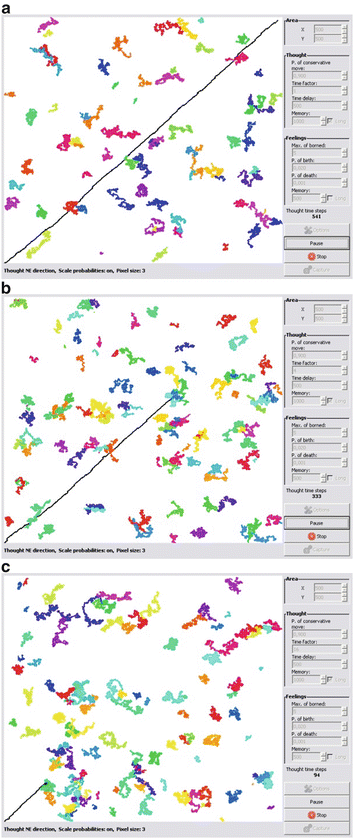
Fig. 1

Preference matrix; columns – subjects (11); lines – objects (22); greenish – rather ‘yes’, p > 0.5; reddish – rather ‘no’, p < 0.5

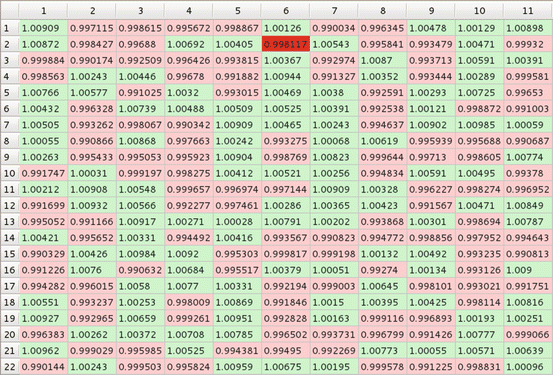
Fig. 2

Impact matrix; columns – subjects (11); lines – objects (22); greenish – rather ‘positive’, i > 1.0; reddish – rather ‘negative’, i < 1.0

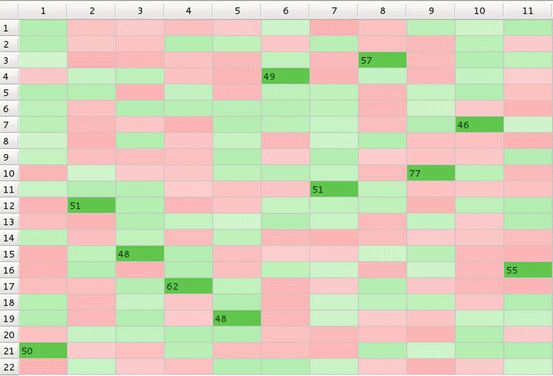
Fig. 3

Natural GoC – ‘monogamic model’ (additional material: mono.mpeg)

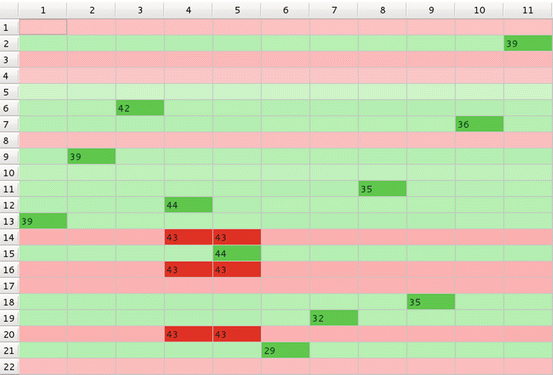
Fig. 4

Controlled GoC with feedback between subjects and the environment and with interactions between subjects (additional material: oenv_m.mpeg)

For example, in Fig. 3, each of 11 subject chose one and only one object (‘mating partner’)’; subject 9, needed 77 repetitions (objects presentations) to make the choice while subject 10 made decision already after 46 presentations. In ‘polygamic model’ on Fig. 5, subject 5, chose as many as six objects (shown in dark green), while several subjects still chose only one object each; moreover subject 7 strongly rejected object 14 (shown in dark red). When interactions between subjects is taken into account objects 3, 4, 8, 14−17, and 22 are rejected by all 11 subjects, with subject 14 being strongly rejected by as many as six subjects (Fig. 6). In Fig. 7, objects belonging to class 7 are chosen by all but two subjects. In a controlled GoC with feedback between subject and environment again, like in simple monogamic case, each subject has chosen one object but rejections are scattered (Fig. 8) while when feedback between subjects is added all subjects reject objects 1, 3, 4, 8, 14, 16, 17, 22. Such situation may be observed rather during elections of MPs then in choosing a mate.

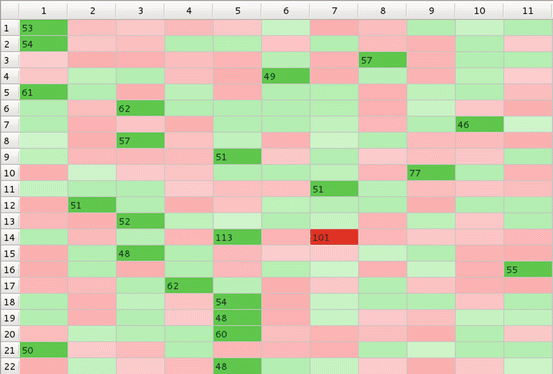
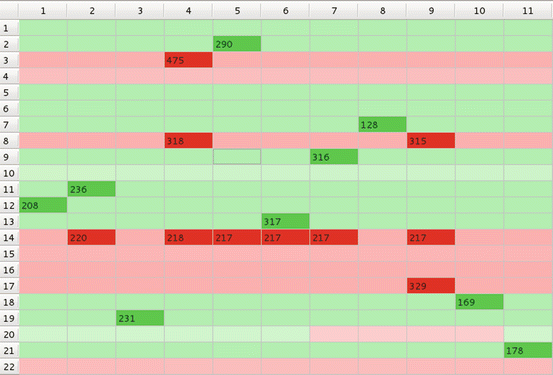
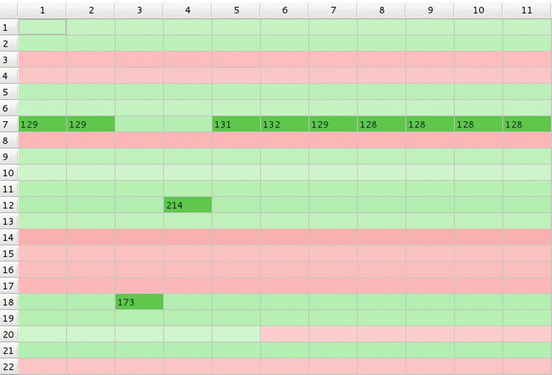
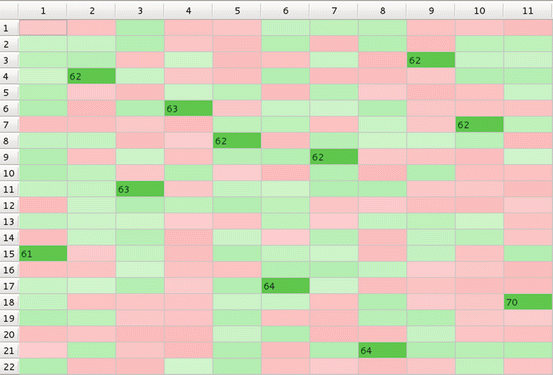
Fig. 5

Natural GoC – ‘polygamic model’ (additional material: poly.mpeg)

Fig. 6

Natural GoC with interaction between subjects (additional material: env_m.mpeg)

Fig. 7

Natural GoC with interaction between subjects with the number of objects in each subclass at least equal to the number of subjects (additional material: ienv_m.mpeg)

Fig. 8

Controlled GoC with feedback between subjects and the environment – without interaction between subjects (additional material: omono.mpeg)

3 Chaosensology Model

In GoC models decisions are based on emotions – a subject does not think logically, comparing ‘pros’ and ‘cons’ for the decision which subject to choose. Our Chaosensology Model (ChS) (from Latin word sensus – feeling, emotion) explains cognitive neurodynamics difference between logical thoughts and emotions. It is inspired by process of occupying biological ‘niches’ by different species – the given niche has to be vacated by one species before it may be occupied by another one. Niches are represented by lattice cells (Figs. 9 and 10). A logical thought represented by black line starting in lower-left cell that tries to move towards upper-right may be blocked because the cells in its front are occupied by randomly coiling colourful emotions (cf. [2]). We assume that τ for logical thoughts is q-times longer than for emotions, and we also change ‘memory parameter’ that is how long a lattice cell remains occupied (cf. Figs. 9 and 10). Similar but statical lattice models with excluded volume effect have been used e.g. for calculating entropy of mixing. Analogically, any neuron may at any given moment takes part in only one brain process and after action potential had been generated the neuron may be ‘vacated’ and after a certain refractory period it may be involved into another brain process.