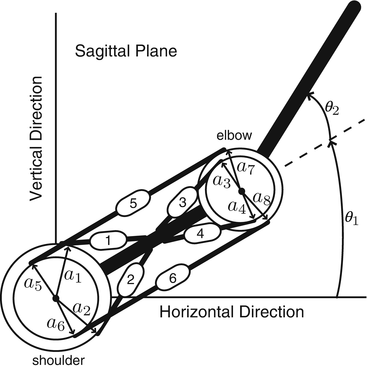
Fig. 4.1
Co-contraction
4.2.3 Joint Stiffness
When joint position moves with the same contraction level, restoring force is generated as shown in Fig. 4.2.
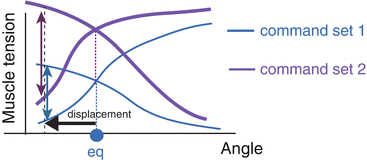

Fig. 4.2
Force generation
The magnitude of this force depends on each muscle’s contraction level. At the same posture, stiffness depends on muscle activation level (Fig. 4.3). The ratio of this restoring force and displacement is called joint stiffness.
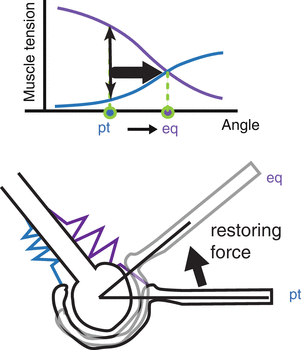
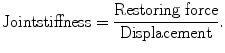 In Fig. 4.1, restoring force is equal, but the displacement is different. In Fig. 4.3, displacement is same, but the restoring force is different. For both cases, joint stiffness of command set 1 is bigger than that of command set 2.
In Fig. 4.1, restoring force is equal, but the displacement is different. In Fig. 4.3, displacement is same, but the restoring force is different. For both cases, joint stiffness of command set 1 is bigger than that of command set 2.

Fig. 4.3
Stiffness
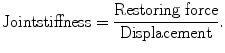
4.2.4 Equilibrium Position Change
To produce a trajectory, it has been hypothesized that the central nervous system (CNS) sends only final posture information, and muscle activities are generated such that the joint is stabilized at the equilibrium position [2] (Fig. 4.4).
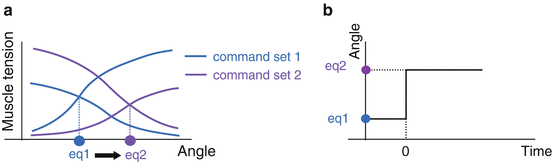

Fig. 4.4
Equilibrium control
To test this hypothesis, Bizzi and colleagues performed an experiment using a deafferent monkey [6]. If the hypothesis were correct, the hand position would move to the end point just before the motion. The hand would be there because the brain (in this hypothesis) sends commands to stabilize the hand at the end position. However, when they did the experiment, they obtained different results. The hand moved to the middle position and then to the end point. They concluded that the brain sends commands to gradually shift the hand to the end point. So it came to be thought that the brain plans trajectory.
4.3 New Control Hypothesis
Though rejected by Bizzi’s experiment, the end point control hypothesis is still attractive because it allows motion control and force control to be treated in the same way. Joint torque is calculated as τ = K(θ eq−θ), where K, θ eq, and θ denote joint stiffness, equilibrium position, and current position, respectively (Fig. 4.5).


Fig. 4.5
Uniform control for motion and force
4.3.1 Uniform Control Hypothesis
As mentioned in the previous section, we can change equilibrium position and stiffness independently. This means that we have a redundant control system. For example, in order to hold an object of weight m in hand, where the distance between the wrist joint and object position is d, and force F equals mg, the wrist must produce a torque of mgd cos θ to compensate for the weight of the object. The brain changes the equilibrium position and stiffness to produce torque τ = K(θ eq−θ). If the object’s weight is known, it is easy to set the equilibrium position and stiffness. For familiar objects, stiffness is set to an appropriately low value, and the brain changes the equilibrium position depending on the object’s weight. If the weight of the object is unknown, stiffness is high, and the difference between the equilibrium position and current position is small. High stiffness allows the hand to be stabilized even if the weight estimation is not completely accurate.
4.3.2 New Hypothesis
The deafferent monkey did not know the current position because proprioceptive feedback was withheld. So the monkey had to control his arm using feedforward control mechanisms and without feedback control. As the monkey’s arm moved forward from the initial position, the brain had to send trajectory information in time which gradually shifted from the initial position to the final position (Fig. 4.6a).
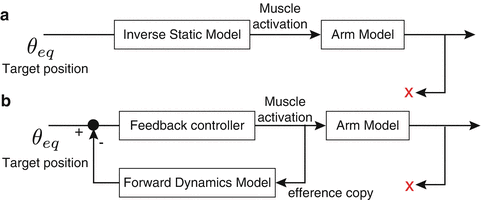

Fig. 4.6
From end point control to equilibrium control hypotheses
However, the brain can use its efference copy, which is a copy of the motor command. Also, the brain has a forward dynamics model of our body, so it can generate sensory feedback signals from the efference copy in the brain. The forward dynamics model is one of the brain’s internal models and its existence has been indicated experimentally. For these reasons, the deafferent monkey would estimate his current position and control his arm using feedback control (Fig. 4.6b).
The end point control hypothesis was rejected by Bizzi’s experiment, but if the existence of a forward dynamics model is assumed, a hypothesis which does not require trajectory planning is still attractive. In daily life, we are not always reaching to the same target. The CNS learns how to generate reaching movements toward various targets in the workspace. However, it is difficult to perform various movements with high accuracy using a single feedback controller. Since the gravitational force acting on the arm depends on the posture of the arm, the force required to hold the hand at the target varies with the target position. Furthermore, the magnitude of muscle tension varies with the posture of the arm, even if a level command signal is sent to the muscle. For these reasons, there is no guarantee that a single feedback controller trained for a particular target would generate accurate reaching movements to other targets (Fig. 4.7).
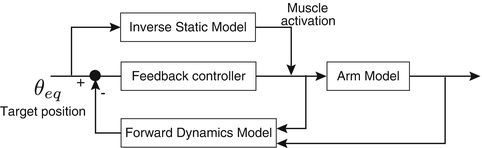

Fig. 4.7
Proposed control system
Here we introduce an additional controller called an inverse statics model, which supports the feedback controller in generating reaching movements toward various targets. It handles the static component of the inverse dynamics of the arm. That is, it transforms a desired position (or posture) into a set of motor commands that leads the hand to the desired position and holds it there. Note that the arm converges to a certain equilibrium posture when a constant set of motor commands is sent to the muscles because of the springlike properties of the musculoskeletal system [7].
However, there are many combinations of flexor and extensor muscle activation levels to achieve the same equilibrium position (Fig. 4.1). This means that a constraint condition is needed for the inverse statics model.
If the inverse statics model is trained properly, it can compensate for the static forces (e.g., gravity) at the target point. Therefore, accurate reaching movements toward various target points are realized by combining the inverse statics model and the feedback controller which works moderately well within the workspace.
4.3.3 Learning Mechanism
The forward dynamics model can be trained in a supervised learning manner since the teaching signal can be obtained from somatosensory feedback.
Reinforcement learning has attracted much attention as a self-learning paradigm for acquiring optimal control strategy through trial and error [8]. In particular, the actor-critic method, one of the major frameworks for the temporal difference learning, has been proposed as a model of learning in the basal ganglia [9, 10]. We adopt the actor-critic method [11] in order to acquire a feedback controller for multi-joint reaching movements.
To acquire an accurate inverse statics model in a trial-and-error manner, the feedback-error-learning scheme [12] was adopted. In this scheme, inverse dynamics (or statics) models of controlled objects are trained by using command outputs of the feedback controller as error signals. This learning scheme was originally proposed as a computational coherent model of cerebellar motor learning. The original model, however, did not explain how to acquire the feedback controller for arm movements. In our model, the actor-critic method is introduced to train the feedback controller. Therefore, our model gives a possible solution to the problem of feedback controller design in the feedback-error-learning scheme.
4.3.4 Estimated Trajectories
Two conditions were used for evaluating the estimated trajectories as an arm model. The arm model is composed of a two-link arm with two joints and six muscles (Fig. 4.8).