Fig. 6.1
Test setup. (a) Anklebot fully attached to a human subject while suspended using a compliant strap. (b) Anklebot partially attached to a human subject while suspended using a compliant strap. (c) Anklebot attached to ankle mockup
To validate this procedure it was also applied to a physical “mockup” of the ankle, consisting of two wooden blocks, one corresponding to the shank, the other to the foot (Fig. 6.1c) and connected at right angles by a stainless steel plate weakened by slots. By design, the rotational stiffness of this plate was highly anisotropic to allow assessment of our method’s ability to detect the directional structure of ankle impedance. The shank block was secured to a horizontal table. A connector similar to that used in the Anklebot shoes was secured to the foot block. To avoid plastic deformation of the steel plates, the magnitude of the random signals used with this mockup was 60 % of the magnitude used with human subjects. For comparison, the inertia of the foot block and the stiffness of the steel plate were estimated from their geometric and material properties.
6.2.4 Analysis Methods
The measured variables were the displacements X L and X R and commanded forces F L and F R in the left and right actuators, respectively. The ankle torques and angles were estimated from a kinematic model of the relation between actuator displacement and joint angular displacement depicted in Fig. 6.2:
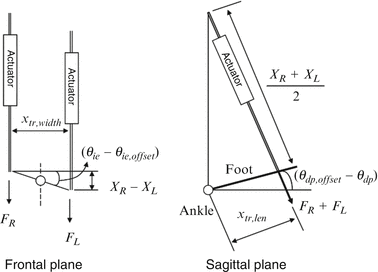
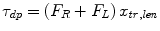
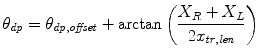
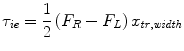

where τ dp and τ ie are joint torques and θ dp and θ ie are angles in DP and IE directions, respectively. θ dp,offset and θ ie,offset are the angles at which the ankle will be centered with respect to the coronal and sagittal planes, respectively. In the experiments in this study, their values were zero. The other parameters in Eqs. 6.1, 6.2, 6.3, and 6.4 are described in Fig. 6.2.

Fig. 6.2
Schematic of Anklebot and its geometrical parameters
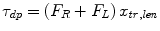
(6.1)
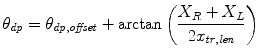
(6.2)
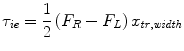
(6.3)

(6.4)
Voltage inputs to the actuators generated forces that resulted in ankle motion. A “natural” or strictly proper description of this system is as a mechanical admittance (force input, motion output). Assuming linear dynamics, admittance Y(f) in DP-IE space is a 2 × 2 matrix of transfer functions.
![$$ \left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\}=\mathbf{Y}(f)\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}=\left[\begin{array}{ll}\hfill {Y}_{11}(f)\hfill & \hfill {Y}_{12}(f)\hfill \\ {Y}_{21}(f)\hfill & \hfill {Y}_{22}(f)\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\} $$](/wp-content/uploads/2016/11/A324794_1_En_6_Chapter_Equ5.gif)
![$$ \left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\}=\mathbf{Y}(f)\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}=\left[\begin{array}{ll}\hfill {Y}_{11}(f)\hfill & \hfill {Y}_{12}(f)\hfill \\ {Y}_{21}(f)\hfill & \hfill {Y}_{22}(f)\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\} $$](/wp-content/uploads/2016/11/A324794_1_En_6_Chapter_Equ5.gif)
(6.5)
If this matrix is non-singular, its inverse is mechanical impedance, Z(f) = Y − 1(f), a matrix of transfer functions relating input angles to output torques.
![$$ \left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}=\mathbf{Z}(f)\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\}=\left[\begin{array}{ll}\hfill {Z}_{11}(f)\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\} $$](/wp-content/uploads/2016/11/A324794_1_En_6_Chapter_Equ6.gif)
![$$ \left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}=\mathbf{Z}(f)\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\}=\left[\begin{array}{ll}\hfill {Z}_{11}(f)\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\} $$](/wp-content/uploads/2016/11/A324794_1_En_6_Chapter_Equ6.gif)
(6.6)
A proportional controller with a diagonal gain matrix with identical elements prevented the ankle from drifting from its neutral position.
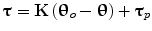
where 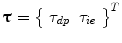 is a vector of applied ankle torques,
is a vector of applied ankle torques, 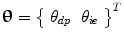 is a vector of ankle angles, K is a diagonal gain matrix that determines Anklebot stiffness that prevents the foot from drifting, subscript o denotes the neutral ankle angle, and subscript p denotes perturbation torques. The ankle and Anklebot form a multivariable closed-loop system.
is a vector of ankle angles, K is a diagonal gain matrix that determines Anklebot stiffness that prevents the foot from drifting, subscript o denotes the neutral ankle angle, and subscript p denotes perturbation torques. The ankle and Anklebot form a multivariable closed-loop system.
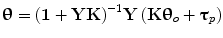
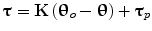
(6.7)
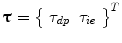 is a vector of applied ankle torques,
is a vector of applied ankle torques, 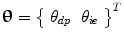 is a vector of ankle angles, K is a diagonal gain matrix that determines Anklebot stiffness that prevents the foot from drifting, subscript o denotes the neutral ankle angle, and subscript p denotes perturbation torques. The ankle and Anklebot form a multivariable closed-loop system.
is a vector of ankle angles, K is a diagonal gain matrix that determines Anklebot stiffness that prevents the foot from drifting, subscript o denotes the neutral ankle angle, and subscript p denotes perturbation torques. The ankle and Anklebot form a multivariable closed-loop system.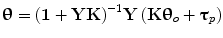
(6.8)
The closed-loop admittance matrix is θ = (1 + YK)− 1 Yτ p . The closed-loop impedance matrix is its inverse, τ p = Y − 1(1 + YK)θ = (Z + K)θ, i.e.
![$$ {\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}}_p=\left[\begin{array}{ll}\hfill {Z}_{11}(f)+ K\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)+ K\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\} $$](/wp-content/uploads/2016/11/A324794_1_En_6_Chapter_Equ9.gif)
![$$ {\left\{\begin{array}{l}\hfill {\tau}_{dp}\hfill \\ {\tau}_{ie}\hfill \end{array}\right\}}_p=\left[\begin{array}{ll}\hfill {Z}_{11}(f)+ K\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)+ K\hfill \end{array}\right]\left\{\begin{array}{l}\hfill {\theta}_{dp}\hfill \\ {\theta}_{ie}\hfill \end{array}\right\} $$](/wp-content/uploads/2016/11/A324794_1_En_6_Chapter_Equ9.gif)
(6.9)
The mechanical impedance of the system under test is
![$$ \mathbf{Z}(f)=\left[\begin{array}{ll}\hfill {Z}_{11}(f)\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)\hfill \end{array}\right]=\left[\begin{array}{ll}\hfill \frac{\tau_{dp}(f)}{\theta_{dp}(f)}- K\hfill & \hfill \frac{\tau_{dp}(f)}{\theta_{ie}(f)}\hfill \\ \frac{\tau_{ie}(f)}{\theta_{dp}(f)}\hfill & \hfill \frac{\tau_{ie}(f)}{\theta_{ie}(f)}- K\hfill \end{array}\right] $$](/wp-content/uploads/2016/11/A324794_1_En_6_Chapter_Equ10.gif)
where the impedance functions τ x (f)/θ y (f) x, y = dp, ie are determined from experimental measurements.
![$$ \mathbf{Z}(f)=\left[\begin{array}{ll}\hfill {Z}_{11}(f)\hfill & \hfill {Z}_{12}(f)\hfill \\ {Z}_{21}(f)\hfill & \hfill {Z}_{22}(f)\hfill \end{array}\right]=\left[\begin{array}{ll}\hfill \frac{\tau_{dp}(f)}{\theta_{dp}(f)}- K\hfill & \hfill \frac{\tau_{dp}(f)}{\theta_{ie}(f)}\hfill \\ \frac{\tau_{ie}(f)}{\theta_{dp}(f)}\hfill & \hfill \frac{\tau_{ie}(f)}{\theta_{ie}(f)}- K\hfill \end{array}\right] $$](/wp-content/uploads/2016/11/A324794_1_En_6_Chapter_Equ10.gif)
(6.10)
Although the system naturally behaves as a mechanical admittance, expressing it as a mechanical impedance simplifies separating the robot dynamics from the human ankle dynamics. The foot and shoe share the same motion, consequently the torque exerted by the actuator is the sum of the torques required to move the foot and shoe; the output mechanical impedance of the robot adds to the human ankle mechanical impedance. The human ankle mechanical impedance is obtained by subtracting the estimate for robot and shoe alone from the estimate for robot, shoe, and ankle as follows.
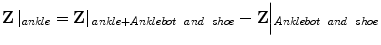
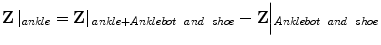
(6.11)
Frequency-domain stochastic methods were used to estimate the mechanical impedance matrices. Sixty seconds of data were sampled at 200 Hz yielding 12,000 samples. Welch’s averaged, modified periodogram method of spectral estimation, as implemented in MATLAB was used to estimate one-sided auto- and cross-power spectral densities of the torque and angle sequences in the DP and IE directions. A periodic Hamming window with a length of 512 samples was used with an FFT length of 1,024 samples, yielding a spectral resolution of 0.195 Hz. Power spectral density functions were estimated by averaging their values calculated from 45 data windows with 50 % overlap (256 samples). The standard error of the impedance plots was determined by dividing the standard deviation of impedances at each frequency by 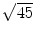 . Elements of the mechanical impedance matrix are presented in Appendix as described in [48]. Moreover, partial coherence functions were estimated to measure the linear dependency between each input and output after removing the effects of the other inputs in the multivariable case (see Appendix).
. Elements of the mechanical impedance matrix are presented in Appendix as described in [48]. Moreover, partial coherence functions were estimated to measure the linear dependency between each input and output after removing the effects of the other inputs in the multivariable case (see Appendix).
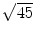 . Elements of the mechanical impedance matrix are presented in Appendix as described in [48]. Moreover, partial coherence functions were estimated to measure the linear dependency between each input and output after removing the effects of the other inputs in the multivariable case (see Appendix).
. Elements of the mechanical impedance matrix are presented in Appendix as described in [48]. Moreover, partial coherence functions were estimated to measure the linear dependency between each input and output after removing the effects of the other inputs in the multivariable case (see Appendix).6.3 Results
6.3.1 Validation Using the Ankle Mockup
Because of the modest torques applied to the physical mockup, its displacements were small (root-mean square actuator displacement was 2.5, 2.4 and 2.3 mm when proportional gains were 5, 10 and 15 Nm/rad, respectively) supporting a linear description of its dynamics. Figure 6.3a shows the partial coherences obtained when the stochastic estimation procedure was applied to the mockup in actuator coordinates (the forces and displacements of the actuators) with proportional gain 10 N-m/rad. The diagonal elements exhibited partial coherences greater than 0.8 at most frequencies from 0 to 50 Hz, averaging 0.86 in the DP and 0.89 in the IE directions over this range. The off-diagonal elements exhibited partial coherences typically greater than 0.8 from 0 to 20 Hz, decreasing to 0.6 at about 30 or 40 Hz and averaging 0.68 from X R to F L and 0.75 from X L to F R from 0 to 50 Hz. These results demonstrated that, despite the known nonlinearities of the Anklebot actuators (including static friction, primarily due to the traction drives, and “cogging” due to the permanent magnet motors [34]), the linear methods we used gave satisfactory results.
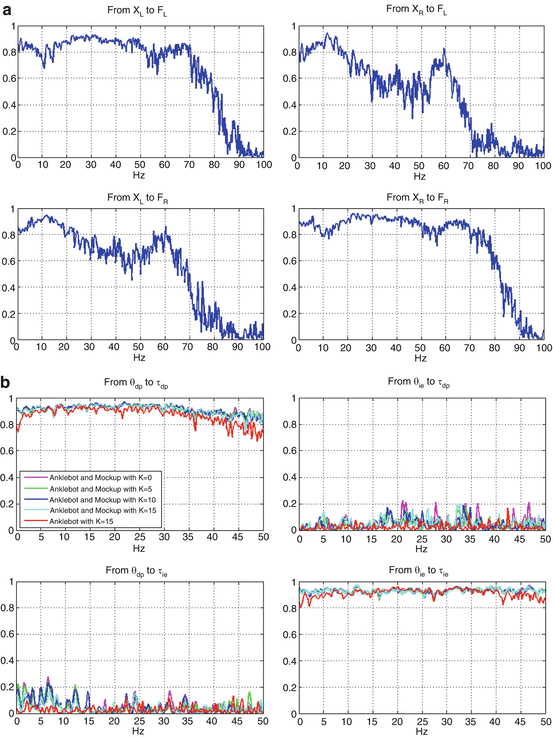

Fig. 6.3
Partial coherences of the mockup impedance matrix, (a) in actuator coordinates; (b) in joint coordinates
Figure 6.3b shows the partial coherences obtained when the recorded data were first transformed to DP-IE joint coordinates (as detailed in Eqs. 6.1, 6.2, 6.3 and 6.4) before applying the stochastic estimation procedure. Results obtained with four values of the proportional gain (K = 0, 5, 10 and 15 N-m/rad) are superimposed, showing that all yielded essentially identical results, along with the results obtained when the actuators were disconnected from the foot block (with K = 5 N-m/rad). In this case, the partial coherences of the off-diagonal elements declined to extremely low values, less than 0.2 at most frequencies, averaging less than 0.05 from θ ie to τ dp and from θ dp to τ ie from 0 to 50 Hz for all values of proportional gain. As shown by the partial coherences in Fig. 6.3a, this cannot be attributed to nonlinear dynamics but is due to low signal strength. By design, there is essentially no coupling between the DP and IE degrees of freedom of the mockup; its impedance matrix is essentially diagonal with zero entries in the off-diagonal positions. Confirming this account, the partial coherences of the diagonal elements increased, becoming greater than 0.8 and close to 0.9 at almost all frequencies between 0 and 50 Hz, averaging more than 0.9 from θ dp to τ dp and from θ ie to τ ie , respectively, over this range for all value of proportional gain, indicating that the diagonal elements of a linear model accounted for more of the data variance in joint coordinates.
Figure 6.4 shows Bode plots of the magnitude and phase of the actuator and mockup diagonal mechanical impedances. The impedance of the actuator alone was as expected. A permanent-magnet motor driven by a current-controlled amplifier is competently modeled as a force-controlled actuator retarded by an output impedance dominated by a combination of inertia and damping, and that is consistent with these observations. The estimated mechanical impedance of the mockup was obtained by subtraction as described above. Results obtained with four values of the proportional gain, K, are superimposed, and demonstrate that the method was extremely insensitive to this parameter.
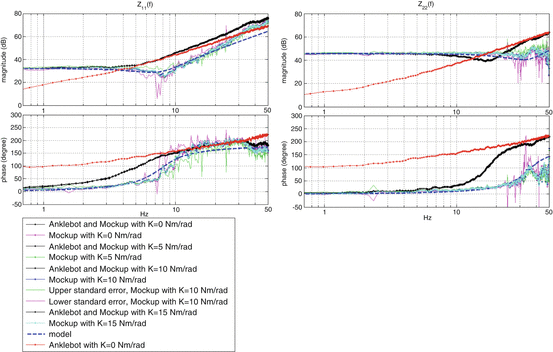

Fig. 6.4
Diagonal elements of the mockup impedance matrix in joint coordinates
A linear second-order model, based on the mockup physical parameters, is also superimposed. In DP the parameter values are inertia: 0.017 kg-m2; damping: 0.4 N-m-s/rad; stiffness: 40.2 N-m/rad. Parameter values in IE are inertia: 0.004 kg-m2; damping: 0.5 N-m-s/rad; stiffness: 191 N-m/rad. The model exhibited an undamped natural frequency at 7.7 Hz in DP.
In IE the undamped natural frequency appears to be at 34.8 Hz. However, in both DP and IE, the phase plots showed evidence of returning towards zero degrees, suggesting the presence of a dynamic zero, which may be due to un-modeled resonance, e.g., due to the metal bracket that was mounted on the foot block. As a result, the data at frequencies greater than 30 Hz should be interpreted with caution. Theoretical calculation of the foot block moment of inertia in the DP direction yielded 0.0176 kg-m2, which differed from the DP model parameter by 3.4 %. Theoretical calculation of the steel plate stiffness in bending yielded 40.0 N-m/rad, which differed from the DP model parameter by 0.5 %.
6.3.2 Human Ankle Mechanical Impedance
6.3.2.1 Coherences
The torques applied to the ankle evoked small angular displacements (root-mean square displacement was 2.48° in DP and 2.70° in IE) consistent with linear analysis. Figure 6.5a shows a representative example of the partial coherences obtained when the stochastic estimation procedure was applied in joint coordinates. Over a frequency range from 0 to 50 Hz, both of the diagonal elements of the impedance matrix exhibited a partial coherence averaging 0.93, with a minimum of 0.84 at 0.78 Hz for Z 11 and 0.87 at 3.12 Hz for Z 21. A proportional gain of K = 10 N-m/rad was used to prevent the ankle from drifting from its neural position. Almost identical results were obtained with proportional gains of K = 5 and 15 N-m/rad. In contrast, over the same frequency range the off-diagonal elements of the impedance matrix exhibited low coherence averaging 0.06. Below 10 Hz the off-diagonal partial coherence improved slightly, peaking at 0.41 at 2.15 Hz for Z 12 and 0.37 at 5.6 Hz for Z 21 but yielding averages over 0 to 10 Hz of 0.19 for Z12 and 0.20 for Z21. As indicated from the validation tests, this indicates weak coupling between DP and IE throughout most of the frequency range.
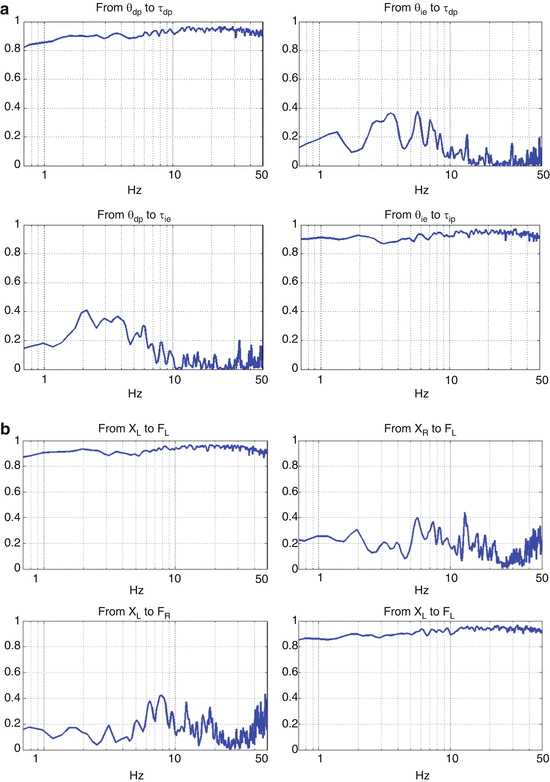

Fig. 6.5




Partial coherence plots of the diagonal elements of the impedance matrix for Anklebot attached to a human ankle with proportional gain K = 10 N-m/rad, (a) in joint coordinates; (b) in actuator coordinates
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree





