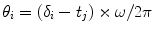Fig. 1
The computational model of the ITD detection neural circuit. The input signal of each ear has the same frequency, and ∆T is the ITD signal
The inner hair cell (IHC) model corresponds to the transfer function Vm = f 1(x) in Fig. 1. The basilar membrane (BM) displacement, a sine waveform, is the input signal (x), the output signal is the membrane potential (Vm) of the inner hair cell. The model is proposed by utilizing a realistic transducer conductance and membrane time constant. It also assumes that the tension-gated channels are the only apical channels [3]. The auditory nerve (AN) model corresponds to the transfer function, FR = f 2(Vm) in Fig. 1. This model is based on Mountain’s work in hearing model research. The final output of this model is the action potential firing rate on the auditory nerve [4]. All the neurons in the ITD detection neural network are presented by the model of Rothman (a realistic biophysical neuron model based on ionic channels) [5]. The main function of the neuron model is shown in Eq. 1. The Rothman model is solved by the fourth-order Runge-Kutta method with the step is 0.02 ms.
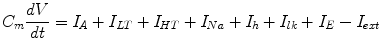
C m is the membrane capacitance of the neuron; V represents the membrane potential of the neuron; I A , I LT , I HT , I Na and I E are ion current; I lk is the leak current; I ext is the external input current.
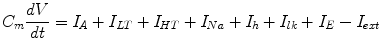
(1)
2.1 Circle Maps in the ITD Detection Model
The displacement in each cochlea BM has the same frequency. The right ear BM displacement signal has a ΔT delay compared to the left one. The output of the ITD model is the spike train of the MSO model. The ITD detection model can be considered as a dissipative dynamical system with two competing frequencies: the input BM displacement signal frequency and the oscillation frequency of MSO neuron. But the ITD detection model is a high dimensional nonlinear model, our quantitative knowledge about highly nonlinear system is meager. In order to analyze the neural coding of the ITD model, first, the complexity of this model should be reduced. Analyzing the interaction between these two frequencies is a effective method to reveal the mechanism of ITD neural coding. Circle map is a valid method to simplify a nonlinear dynamic system [6, 7].
Through the following operations, we can get the circle map of the ITD detection model.
In the ITD detection model, the variable θ n represents the phase of the MSO spike train measured stroboscopically at periodic time point, t n = 2πn/ω from the periodic input BM displacement (x 1 = Asin(ωt) in Fig. 1). A phase shift θ n → θ n + 1 represents a full rotation. Due to the complexity of the ITD model, the system function θ n + 1 = f(θ n ) is difficult to express. But with the evolution of iterations of the circle maps, the phase train θ, f(θ), f 2(θ), …, are computed. The detailed steps are as follow. The time point train t 1, t 2, …, t n is the periodic time point from the input signal x 1 = A sin(ωt) . The firing time of the spike train is recorded and denoted as δ 1, δ 2, … δ n . δ i is the time of ith spike of the MSO neuron. The spike phase, θ i , is as follows: