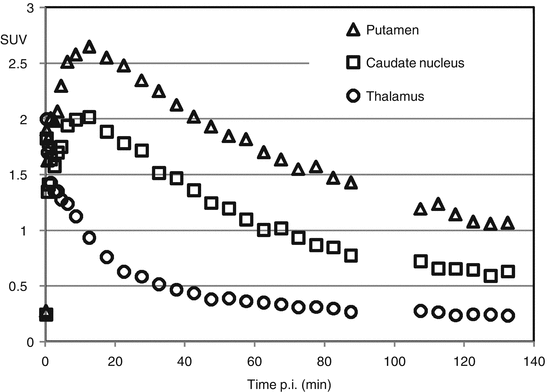
Fig. 2.1
Time-activity curves of a PET tracer targeting PDE10A (Van Laere et al. 2013) for the putamen, caudate nucleus, and thalamus. (a) represents an average SUV image (averaged over 60–90 min interval), (b) the corresponding T1-weighted MRI dataset with delineated brain structures, (c) the co-registered MR and PET dataset, and (d) the PET dataset with the brain structures transferred from the registered MR dataset
Since each PET probe is characterized by its particular kinetic behavior in the brain, understanding its dynamics and quantification is a critical component for designing imaging protocols, setting up clinical studies and interpreting results.
2.2 Dynamic PET Quantification
In vivo quantification of molecular targets with PET imaging is complicated due to the fact that tracers are administered intravenously and not directly applied to the target tissue. Therefore, delivery of the tracer to the brain is influenced by the local blood flow, free tracer concentration in the plasma, and peripheral tracer clearance due to metabolization and excretion. Moreover, total brain activity is measured with PET brain imaging, while often specifically bound, nonspecifically bound, and free tracer need to be separated to estimate the specific tracer signal. For the remainder, we assume that appropriate algorithms have been used to reconstruct a quantitative, accurate radiotracer distribution such that image values are proportional to the radiotracer concentration in brain tissue. We will focus on the accurate quantification of the particular neurobiological function targeted by the radiotracer. Therefore, three essential aspects are to be considered. On the one hand, dynamic PET data characterize the kinetic behavior of the PET tracer in brain tissue, while, on the other hand, an input function is needed to describe the time-dependent amount of tracer that is delivered to the brain tissue. Third, relatively complicated mathematical analysis will model the tracer kinetics on basis of the dynamic PET data and an input function.
Dynamic PET image data are binned and reconstructed into various time frames and represent the radiotracer distribution in tissue at specific time points throughout the PET study. This temporal evolution of radiotracer concentration in individual voxels or regions of the image volume is called a time-activity curve (TAC). These TACs form the basis in quantifying the physiological (e.g., blood flow) and/or pharmacological aspect (e.g., receptor binding site density, enzyme activity) of the system of interest.
To generate TAC for specific brain regions of interest, PET data can be aligned with corresponding MRI data by optimizing translation and rotation parameters. This way high-resolution anatomical MR information can be used to facilitate manual delineation of the appropriate volume-of-interest (VOI) especially when the PET data itself provide limited anatomical landmarks (see Fig. 2.1).
While manual delineation can be time-consuming and observer dependent, methodologies have been developed that allow automatic VOI generation (Svarer et al. 2005). These methods create an individualized VOI probability map on the basis of a database of several MRI datasets, where a VOI template has been defined manually on each MRI dataset. Nonlinear image registration between these MRI datasets and the MRI dataset of interest allows transfer of these individually defined VOI templates to the MRI dataset of interest. Based on the degree of overlap of the transferred VOI sets, a VOI probability map is created specifically for that particular PET dataset. When the generated VOI map is based on more than one template VOI set, VOI delineation proved to be better reproducible and showed less variation as compared to manual delineation or transfer of only a single VOI template. This methodology allows a fast, objective, and reproducible assessment of regional brain PET values.
In addition, the latter methodology offers the possibility to correct for partial volume effects in brain PET imaging. Due to the limited resolution of PET imaging, a PET voxel is only partly composed of the target brain tissue which in most cases is a specific grey matter brain structure. Therefore, the PET signal actually reflects the activity concentration of different underlying adjacent tissue types like the grey matter, white matter, and cerebrospinal fluid. Because of differences in activity concentration between these tissue compartments, the PET signal of the target tissue is confounded. One can correct for this partial volume effect by using spatial distribution maps for the white matter, grey matter, and cerebrospinal fluid generated from segmented co-registered MRI data. Taking into account the resolution of the PET system, it is possible to estimate the different underlying tissue fractions for each PET voxel and apply an appropriate correction and weighting of the PET signal (Rousset et al. 2007). This way, the actual tracer uptake per unit grey matter tissue can be determined. This especially applies when comparing healthy volunteers with elderly subjects or with patients suffering from psychiatric disorders where the presence of regional cerebral atrophy is suspected.
In terms of mathematical analysis, brain uptake of a radioactive tracer is often described within the theoretical framework of compartments. Compartment modeling allows description of systems that vary in time but not in space as one of the assumptions for compartmental modeling is that there are no spatial concentration gradients within each department but only gradients in time. In fact, a compartment represents a unique state of the tracer and is defined as a space with separate uptake and clearance rate constants where the radioactive tracer concentration is assumed homogeneous. Rate constants of each compartment are assumed time invariant at least over the duration of the study and considered being representative for the steady state of the system and the properties of the ligand. A compartment may have a physical analog such as interstitial fluid compartment but can also be considered as a tracer being in bound or unbound state. Once the exchange paths between compartments have been specified, the mass balance for each compartment can be described as a set of ordinary differential equations where one differential equation corresponds to an unknown tracer concentration. Tracer concentration in the vascular arterial compartment drives the model taking into account that tracer tissue concentrations are zero at the start of the PET study.
The first compartmental model that was described is the diffusion model for regional cerebral perfusion PET imaging (Frackowiak et al. 1980).
2.3 Compartmental Modeling of Brain Perfusion
PET can be used to study neuronal activation by measuring the changes in regional cerebral perfusion and local large vessel blood flow since changes in neuronal activity are very closely related to perfusion. These PET studies use blood flow tracers like water or butanol which enter brain tissue via diffusion Perhaps it is worthwhile noticing that the term perfusion is used to distinguish the blood flow per unit tissue from the physical flow (ml/min), although the term flow and perfusion has been used interchangeably in the literature.
Kety and Schmidt first described this basic exchange model for nonradioactive substances using the Fick principle (Kety and Schmidt 1948). The Fick principle states that when a fluid with known flow F runs through a compartment which is in steady state, the rate at which substance is extracted from the fluid by the compartment is equal to the difference in concentration when entering and leaving the compartment. Applying this principle to the passage of tracer within capillaries and considering the smallest scale such that the blood compartment represents a single capillary and the compartment is the tissue in the immediate vicinity (see Fig. 2.2), the change in tracer concentration in tissue C T can be described as difference in tracer concentration between arterial blood C A and venous blood C V:
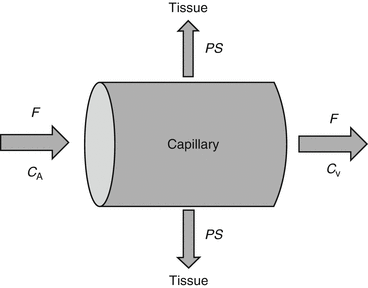

Fig. 2.2
Schematic overview of the exchange of a substance between capillary and tissue where C A denotes the concentration of a substance in arterial blood, C V the concentration in the venous blood, F the flow (units per min), and PS the product of the permeability P (cm/min) and the surface S (cm2/g) of the capillary
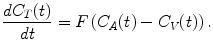
(2.1)
In this context, the partition coefficient ρ was defined as the ratio of the tissue to venous blood concentration. For tracers with high extraction, one can assume that tracer concentration in the venous blood will be in equilibrium with the tissue concentration. Therefore, the tracer concentration in tissue C T is described by
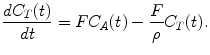
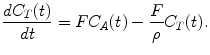
(2.2)
Since tracer concentration can be measured in arterial blood and in tissue and one typically assumes that the same input function is valid for all brain tissue, Eqn. (2.2) can be solved for blood flow and partition coefficient as a function of tissue and arterial blood concentration. Note that this model is only valid when blood flow remains constant during PET imaging and the PET tracer is inert and rapidly and freely diffusible in brain tissue.
2.4 One-Tissue Compartmental Model
The partition coefficient in the context of high extraction tracers can be defined more generally as the ratio of the steady-state concentrations between two compartments and is numerically identical to the tissue volume of distribution V T. The distribution volume is often used in PET literature and is defined as the apparent volume a tracer would occupy, if the tracer were to adopt the same concentration in tissue as in blood. In steady-state PET studies where tracer is delivered via constant infusion in order to maintain tracer concentration in the arterial blood at a constant level, the distribution volume is easily derived from constant concentration ratios in equilibrium. In dynamic PET studies, however, we measure time-dependent concentrations. Assuming that the system is in steady state and the so-called tracer assumption is valid that tracer concentration is negligible, the degree of substance exchange (such as transport through one or more membranes, enzymatic conversions, or binding to specific sites) between kinetically defined “compartments” is proportional to the concentration and can be quantified by rate constants, and rate constants between kinetic compartments are estimated. From these rate constants, the distribution volume can be derived as well. However, if we want to estimate the rate constants, we need to take into account that PET measures all activity present in the field of view, both intra- and extravascular. Thus, the total activity concentration measured by the PET system C PET(t) is given by
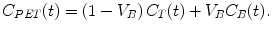
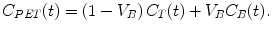
(2.3)
V B represents the blood fraction present in the field of view (0 ≤ V B ≤ 1) and C B(t) the activity concentration in the whole blood, while C T(t) stands for the activity concentration in brain tissue. For the human brain, the assumption that blood occupies about 5 % of the brain volume is valid (Phelps et al. 1979), corresponding to a V B value of about 0.05.
Considering a one-tissue compartment model for describing the bidirectional flux of tracer between blood and tissue, this model is characterized by the time-varying tracer concentration in tissue C T(t) and the arterial blood C A(t) and two first-order kinetic rate constants K 1 and k 2. This way the tracer flux from blood to tissue is K 1 C A, while the tracer flux from tissue to blood is k 2 C T. Therefore, the net tracer flux into tissue is describes as
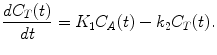
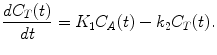
(2.4)
C T(t) represents the radioactivity concentration that is measured with PET in a given brain region, while blood samples may be drawn during the PET measurement in order to measure C A(t).
If we consider tracer exchange on its smallest scale between a blood capillary and the surrounding tissue (see Fig. 2.2), the fraction that is extracted during one capillary pass is equal to
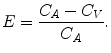
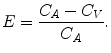
(2.5)
If we take into account the boundary condition that during the first pass of tracer through tissue the tracer flux from tissue to blood is effectively zero because C T(0) = 0 and apply this boundary condition to (2.1) and (2.4), the following equation is valid:
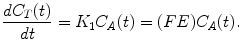
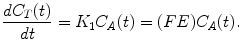
(2.6)
This indicates that the delivery rate constant K 1 equals the product of blood flow and first pass extraction fraction. Considering the capillary as a cylindrical tube, the extraction fraction can be interpreted using the Renkin-Crone capillary model (Crone 1963; Renkin 1959) which states that
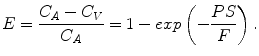
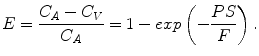
(2.7)
In this equation, P is the permeability of the capillary membrane and S is the capillary surface area per unit tissue mass. Using this approximation the following equation for K 1 is valid:
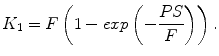
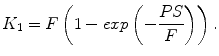
(2.8)
This means that K 1 is closely related to blood flow when the extraction fraction is large (PS >> F) but is more related to permeability when the extraction fraction is low. Accordingly, the best tracers for studying blood flow have a large extraction fraction. For a freely diffusible tracer, K 1 equals perfusion and the ratio 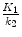 equals the partition coefficient ρ. In a more general context, if we consider tracer concentrations in blood and tissue in equilibrium, a state with no net transfer of tracer between the two compartments, the gradient
equals the partition coefficient ρ. In a more general context, if we consider tracer concentrations in blood and tissue in equilibrium, a state with no net transfer of tracer between the two compartments, the gradient 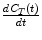 in (2.4) can be set to zero and the following equation for the distribution volume V T is valid:
in (2.4) can be set to zero and the following equation for the distribution volume V T is valid:
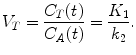
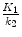 equals the partition coefficient ρ. In a more general context, if we consider tracer concentrations in blood and tissue in equilibrium, a state with no net transfer of tracer between the two compartments, the gradient
equals the partition coefficient ρ. In a more general context, if we consider tracer concentrations in blood and tissue in equilibrium, a state with no net transfer of tracer between the two compartments, the gradient 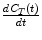 in (2.4) can be set to zero and the following equation for the distribution volume V T is valid:
in (2.4) can be set to zero and the following equation for the distribution volume V T is valid: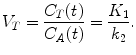
(2.9)
2.5 Two- and Three-Tissue Compartment Model
Partition coefficient ρ or distribution volume V T can be considered as a potential quantitative endpoint of PET tracer uptake in the brain. However, for ligand-receptor PET studies, the law of mass action is applicable to ligand-receptor interaction, and under equilibrium conditions, the following equation is valid:
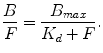
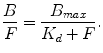
(2.10)
In this equation, B represents the tracer concentration bound to the receptor, and F denotes the free tracer concentration near the receptor, while B max refers to the receptor density and 1/K d to the ligand affinity for the receptor (K d is ratio of the dissociation constant k off over the association constant k on). Since PET imaging typically involves the injection of a very limited amount of ligand mass dose, the concentration of free radiotracer is such that F << K d , resulting in the following equation:
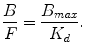
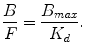
(2.11)
This equation actually corresponds to the binding potential (BP) defined as the product of receptor density and affinity. In terms of PET imaging, this means that BP can be estimated as the equilibrium ratio of specifically bound tracer to free tracer and can be considered as a quantitative endpoint for ligand-receptor studies.
For radioligands that pass the blood–brain barrier by passive diffusion, one can reasonably assume that under equilibrium conditions, the concentration free tracer in arterial plasma equals the concentration free tracer in brain tissue. However, to estimate the concentration of specifically bound tracer, a one-tissue compartment model needs to be extended to a kinetic model containing multiple compartments. The most generalized kinetic model describing ligand-receptor kinetics consists of 3-tissue compartments (see Fig. 2.3), taking into account the activity concentration in arterial plasma C P, the concentration of free radioligand in tissue C F, the concentration of tracer that bounds specifically C S, and the concentration of tracer that does not bound specifically C NS, and therefore is not available for specific binding to the targeted receptor. In this context, K 1 and k 2 represent the transport rate constants between arterial plasma and tissue through the blood–brain barrier, and k 3 and k 4 describe the rate of specific binding and target release of the tracer, while k 5 and k 6 represents the exchange rate constants between the free tracer compartment and nonspecifically bound compartment. For a three-tissue compartment model, the activity concentration in brain tissue C T(t) is given by
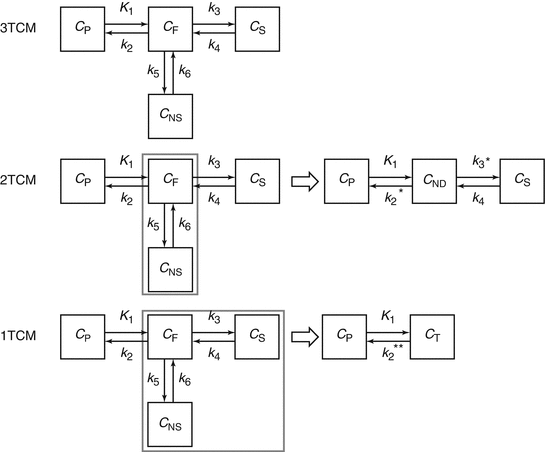
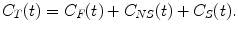

Fig. 2.3
Overview of the different compartment models: a three-tissue compartment model (3TCM) with C P the activity concentration in arterial plasma, C F the concentration of free radioligand in tissue, C S the concentration of tracer that is bound specifically and C NS the concentration of tracer that is bound nonspecifically, K 1 and k 2 represent the transport rate constants between arterial plasma and brain tissue, k 3 and k 4 represent the exchange rate constants between specific binding and the unbound state, while k 5 and k 6 represents the exchange rate constants between the free tracer and nonspecific binding. A two-tissue compartment model (2TCM) with C P the activity concentration in arterial plasma, C ND the concentration of non-displaceable radioligand in tissue, C S the concentration of tracer that is bound specifically, K 1 and k 2* represent the transport rate constants between arterial plasma and brain tissue, and k 3* and k 4 represent the exchange rate constants between specific binding and the free and nonspecifically bound state. A one-tissue compartment model (1TCM) with C P the activity concentration in arterial plasma, C T the tracer concentration in tissue, and K 1 and k 2* * represent the transport rate constants between arterial plasma and brain tissue
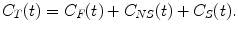
(2.12)
If we formulate the differential equations for the unknown tissue concentrations C F(t), C NS(t), and C S(t), we get the following equations:
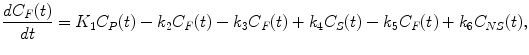
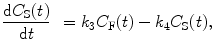
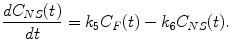
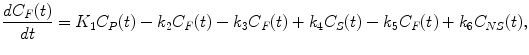
(2.13)
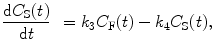
(2.14)
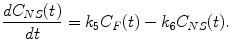
(2.15)
Considering the equilibrium condition where no net exchange between compartments is observed, gradients in (2.13), (2.14) and (2.15) can be set to zero. Substitution of (2.14) and (2.15) in (2.13) yields the following equations for the distribution volume of free tracer, specific bound tracer, and nonspecific bound tracer:

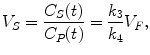
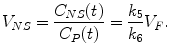

(2.16)
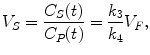
(2.17)
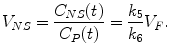
(2.18)
The total volume of distribution for brain tissue V D can be written as
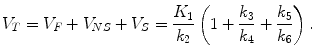
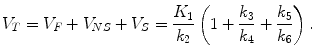
(2.19)
If we consider equilibrium conditions for (2.14) and compare with (2.11), the following equation is valid:
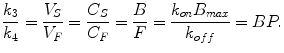
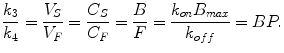
(2.20)
This means that BP can be estimated once the rate constants k 3 and k 4 are determined. Moreover, the rate constant k 3 is dependent on the density of available receptor sites and the ligand-receptor association constant k on, while k 4 equals the ligand-receptor dissociation constant k off.
When the transport rate constants k 5 and k 6 are high such that there is a fast equilibrium between the free tracer and nonspecifically bound tracer compartment, the two compartments are kinetically indistinguishable and can be lumped together into one compartment representing the non-displaceable tracer concentration C ND(t) = C F(t) + C NS(t). This model reduction yields a two-tissue compartment model with the following differential equations describing this model:
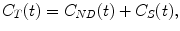
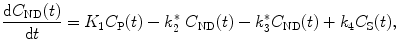
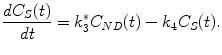
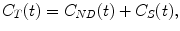
(2.21)
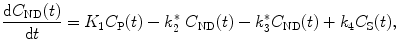
(2.22)
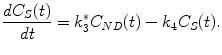
(2.23)
The corresponding tissue distribution volume is given by
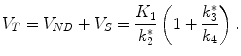
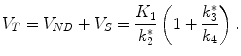
(2.24)
In this case the quantitative parameter of interest is the non-displaceable binding potential BPND defined as
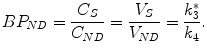
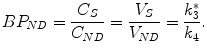
(2.25)
It is worthwhile noticing that the non-displaceable binding potential BPND is defined relative to the concentration non-displaceable radiotracer, whereas the binding potential BP is defined relative to the concentration free radioligand (Innis and Carson 2007). In cases where nonspecific tracer binding could be excluded, BP and BPND are identical. Model reduction to a two-tissue compartment model is usually necessary for the kinetic analysis of dynamic PET data. This way, the number of unknown variables is reduced and more reliable estimates of the exchange rate constants can be achieved.
When the rate constants k 3* and k 4 of a two-tissue compartment are high compared to transport rate constants K 1 and k 2*, a fast equilibrium is achieved between the non-displaceable and specifically bound tracer compartment. In this case a further reduction to a single-tissue compartment is possible where kinetics described by (2.4) and (2.9) are valid.
If a specific brain region is devoid of receptors, the brain tissue of that region can be considered reference tissue. Consequently, BPND can be estimated for any target region using the tissue distribution volumes of reference and target tissue as follows:
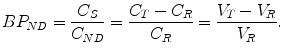
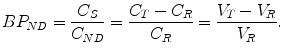
(2.26)
C T and V T, respectively, represent the tracer concentration and distribution volume of the target region, while C R and V R, respectively, represent those of the reference region. It is worthwhile noticing that in this context 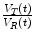 is often termed the distribution volume ratio (DVR) such that BPND = DVR − 1.
is often termed the distribution volume ratio (DVR) such that BPND = DVR − 1.
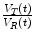 is often termed the distribution volume ratio (DVR) such that BPND = DVR − 1.
is often termed the distribution volume ratio (DVR) such that BPND = DVR − 1.We need to point out that in the absence of a reference region, BP or BPND can be estimated numerically but this estimate is often not reliable. The quantitative parameter that is used most frequently in the absence of reference tissue is the distribution volume V T which can be estimated more reliably.
Equation (2.26) is valid if the tracer concentration in the reference region represents the non-displaceable tracer concentration and if the non-displaceable tracer concentration is the same for both reference and target region. If there is nonspecific tracer binding in the reference tissue and this nonspecific binding can again be assumed the same for both reference and target tissue, the binding potential BPND calculated from tissue distribution volumes will be biased. Taking into account the distribution volumes of both tissues, one gets the following equation:
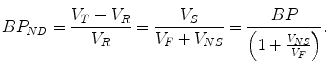
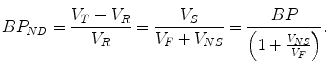
(2.27)
Assuming that the level of nonspecific binding is relatively constant, the bias should be limited to only a scaling factor.
2.6 Model Selection
The choice of a specific model configuration is governed by various factors including the properties of the tracer. To facilitate quantification radiotracers need to have appropriate chemical characteristics. For tracers that cross the blood–brain barrier via passive diffusion, a low molecular weight is mandatory. Lipophilicity of the tracer should be within the small range of allowing adequate permeability of the blood–brain barrier while avoiding unacceptable binding to plasma proteins or high levels of nonspecific binding in the brain. Finally, a high affinity ligand is needed to provide high levels of specific binding to the receptor. However, affinity of the tracer should be such that the opposing goals of high specific binding and washout of the brain are balanced.
If the tracer is inert and does not interact with any receptor system or does not undergo any chemical change, but simply diffuses into and back out of the cells, a one-tissue compartment model would be an appropriate model.
If a one-tissue model is not appropriate, the reversibility of a tracer or in other words the retention of the tracer in the target tissue must be considered prior to choosing the model configuration. Reliable estimates of receptor levels in the brain require both uptake and washout phases of the tissue time-activity curve. Therefore, the tissue clearance of the tracer must typically be matched with the half-life of the radionuclide. This tissue clearance rate is in part determined by the affinity of the tracer and the receptor density. Ligands with higher affinity targeting a rather dense population of receptors tend to stick longer to the target molecules such that washout is delayed beyond the usable measurement time of the radionuclide. If the affinity is such that the radioligand shows very modest washout from the brain during the course of the PET measurement, then the washout rate cannot be determined reliably and critical kinetic data are unavailable to calculate tissue distribution volume V T, BP, or BPND. In terms of transport rate constants, this means that a reliable estimation of the k 4 parameter describing the conversion from the tracer trapped in the bound state back to the nonspecific state is not feasible. In this case and in cases where the tracer is metabolized and the metabolized state is retained in the brain tissue, the tracer can be considered to bind irreversible and k 4 of (2.23) can be set to zero. Instead of V T, BP, or BPND, the influx rate constant K i, also named metabolic rate, trapping rate, or accumulation rate constant, can be considered as an endpoint. K i is defined as
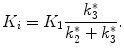
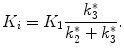
(2.28)
This assumption is, for instance, valid for measuring energy metabolism with 2-fluoro-2-deoxy-d-glucose labeled with the fluorine radioisotope 18F ([18F]-FDG). The substance is glucose analog that is trapped in brain tissue by being metabolized in the mitochondria to FDG-6-PO4 by the hexokinase enzymatic action. For a PET measurement time of less than 1 h post injection, dephosphorylation (k 4) of the FDG-6-PO4 is not observed (Lucignani et al. 1993) and the assumption that k 4 = 0 is valid.
For radioligands with irreversible kinetic behavior, late static scanning can be considered (as is common for [18F]-FDG PET) while these radioligands often provide high specific to nonspecific tracer concentration ratios. However, taking into account (2.28), a high affinity in terms of a large k 3* means that influx rate constant K i becomes proportional to K 1 and thus dependent on tracer transport rate from blood to the brain tissue. This way, K i becomes less dependent of the parameter of interest k 3* and therefore less sensitive to changes in binding site density. On the other hand, the slower equilibrium due to the slower irreversible kinetics of high affinity tracers imposes longer PET acquisition times to quantify potential changes in binding density as accurate as possible. However, quantification can be confounded by radio-metabolites entering the brain tissue. Many tracers currently used for imaging studies produce to some extent lipophilic metabolites. However, the quantities produced or their kinetics for passing the blood–brain barrier are such that they do not commonly confound the PET measurements. In cases where uptake and washout of the parent tracer are fast relative to the production and accumulation of radio-metabolites in plasma, their component of the total measured activity may be negligible during the imaging study. However, for longer PET acquisition times, lipophilic radio-metabolites may enter the brain in sufficient concentration to confound the PET signal.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree





