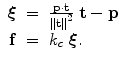Fig. 12.1
The KINARM robot (a) used in this study has a two-degree-of-freedom planar exoskeleton for each arm (only right arm shown for clarity). The user sits in a chair (b) that is positioned so that the user’s hand location and targets are visible on a horizontal display. The seat height, linkage lengths, and arm tray positions are adjusted for each user (c). Special care is taken to ensure that the rotational axes of the human shoulder and elbow are coincident with the corresponding joints of the KINARM. An advantage of the exoskeletal nature of the robot is that robot linkage and human arm kinematic parameters are determined simultaneously
12.2.1 KINARM Robot Motor and Controller Performance Characterization
In order to rigorously examine hypotheses about the function of the cerebellum, we require knowledge of actual limb dynamics and precise measurements of user reaching performance. Our studies used the KINARM robotic exoskeleton (Fig. 12.1, BKIN Technologies, Kingston, ON). The KINARM is an adjustable exoskeleton that permits bimanual shoulder and elbow rotation in the horizontal plane. This device has been used to acquire behavioral data during reaching [29]. In [15], a kinematic and dynamic model of the human arm and robot were developed and populated with parameter values obtained through direct measurement, system identification, and use of anthropometric tables. This provides a relationship between motor effort and movement.
The motors of the KINARM are controlled in an open-loop fashion. In order to understand the limits of the system’s performance, we characterized the ability of motor controllers to follow a desired torque trajectory. Accurate calibration of motor gains is critical for accurate rendering of dynamic forces. For example, consider attempting to render arm inertia (mass matrix with non-negative scalars a, b, and c) while the shoulder and elbow motors have the non-unity gains ζ 1 and ζ 2. This torque scaling results in a corresponding scaling of the mass matrix:
![$$\displaystyle{ \left [\begin{array}{c} \tau _{1_{act}} \\ \tau _{2_{act}}\\ \end{array} \right ] = \left [\begin{array}{cc} \zeta _{1}a&\zeta _{1}b \\ \zeta _{2}b &\zeta _{2}c\\ \end{array} \right ]\left [\begin{array}{c} \ddot{\theta }_{1}\\ \ddot{\theta }_{ 2}\\ \end{array} \right ]. }$$](/wp-content/uploads/2016/11/A324794_1_En_12_Chapter_Equ1.gif)
If 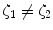 , then the mass matrix is no longer symmetric – in essence, it no longer corresponds to any physically realistic inertia. In such a case, there would be no symmetry between the interaction torques of connected joints. A one-dimensional analog is a mass that feels heavier when moved forward than when moved backward.
, then the mass matrix is no longer symmetric – in essence, it no longer corresponds to any physically realistic inertia. In such a case, there would be no symmetry between the interaction torques of connected joints. A one-dimensional analog is a mass that feels heavier when moved forward than when moved backward.
![$$\displaystyle{ \left [\begin{array}{c} \tau _{1_{act}} \\ \tau _{2_{act}}\\ \end{array} \right ] = \left [\begin{array}{cc} \zeta _{1}a&\zeta _{1}b \\ \zeta _{2}b &\zeta _{2}c\\ \end{array} \right ]\left [\begin{array}{c} \ddot{\theta }_{1}\\ \ddot{\theta }_{ 2}\\ \end{array} \right ]. }$$](/wp-content/uploads/2016/11/A324794_1_En_12_Chapter_Equ1.gif)
(12.1)
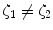 , then the mass matrix is no longer symmetric – in essence, it no longer corresponds to any physically realistic inertia. In such a case, there would be no symmetry between the interaction torques of connected joints. A one-dimensional analog is a mass that feels heavier when moved forward than when moved backward.
, then the mass matrix is no longer symmetric – in essence, it no longer corresponds to any physically realistic inertia. In such a case, there would be no symmetry between the interaction torques of connected joints. A one-dimensional analog is a mass that feels heavier when moved forward than when moved backward.12.2.1.1 Static Performance
To calibrate the static motor gains, the peak motor torque for each link was measured using a single-axis, hand-held digital force gauge (SHIMPO model FGV-50XY, Japan). The sensor was mounted tangentially to the robot link and coupled via a fitting that could not transmit substantial torque to the linkage. Thus, the reaction torque is the measured force multiplied by the moment arm. The torque trajectory was repeated four times at five different amplitudes for each motor.
12.2.1.2 Single-Joint Dynamic Performance
Next, the motor controller’s performance while commanding velocity- or acceleration-dependent loads (viscosity/inertia) was characterized. The velocity, 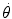 , and acceleration,
, and acceleration, 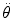 , signals are derived from a high-resolution encoder signal that is discretely differentiated. The process of differentiation scales the high-frequency (noise) content of a signal. To mitigate this effect, a running-average digital filter was used. This window must be larger to filter the acceleration signal compared to velocity.
, signals are derived from a high-resolution encoder signal that is discretely differentiated. The process of differentiation scales the high-frequency (noise) content of a signal. To mitigate this effect, a running-average digital filter was used. This window must be larger to filter the acceleration signal compared to velocity.
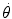 , and acceleration,
, and acceleration, 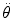 , signals are derived from a high-resolution encoder signal that is discretely differentiated. The process of differentiation scales the high-frequency (noise) content of a signal. To mitigate this effect, a running-average digital filter was used. This window must be larger to filter the acceleration signal compared to velocity.
, signals are derived from a high-resolution encoder signal that is discretely differentiated. The process of differentiation scales the high-frequency (noise) content of a signal. To mitigate this effect, a running-average digital filter was used. This window must be larger to filter the acceleration signal compared to velocity.The actual output torques were measured using an ATI Mini40 force/torque sensor (ATI Industrial Automation, Inc., Apex, NC; SI-20-1 calibration) mounted as before while the robot forearm was manipulated manually to follow a roughly sinusoidal position trajectory. The accuracy of the rendering was assessed by comparing the torques and kinematics using ordinary-least-squares regression [16]. If the desired coefficients for friction and inertia are f b and I, the appropriate torque command τ com is given by (12.2). Even when rendering only inertial or viscous forces, the robot’s inherent inertia and friction contribute to the force/acceleration relationship. As such, objective function (12.3) was used in all cases.
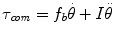
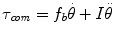
(12.2)
![$$\displaystyle\begin{array}{rcl} \left [\begin{array}{*{10}c} \tau (t_{1}) \\ \tau (t_{2}) \\ \tau (t_{3})\\ \vdots \end{array} \right ]& =& \left [\begin{array}{*{10}c} \theta (t_{1})&\dot{\theta }(t_{1}) \\ \theta (t_{2})&\dot{\theta }(t_{2}) \\ \theta (t_{3})&\dot{\theta }(t_{3})\\ \vdots & \vdots \end{array} \right ]\left [\begin{array}{c} f_{b} \\ I\\ \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_12_Chapter_Equ3.gif)
(12.3)
12.2.1.3 Multi-joint Dynamic Performance
In the first experiment, the KINARM is used to render the change in arm inertia predicted to help each patient. With active use of the robot, the mass matrix is composed of:
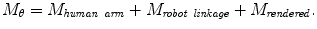
Excessive noise or delay of the acceleration signal may result in poor rendering or instability. To reduce the noise and delay of the acceleration signal, two 2g 3-axis accelerometers (Crossbow Technology, Inc., San Jose, CA) were incorporated into each arm. Though substantially reduced, the residual noise presents an increasing challenge to system performance as the magnitude of the rendered inertia increases. Predicting whether some amount of rendered inertia will be achievable is a formidable problem because it depends on the robot setup and the patient’s size, muscle tone, movement pattern, etc. As such, the rendered inertia must be gradually increased (ε → 1 in (12.5)) while the onset of noise or instability is monitored. It can be shown that any value of 0 < ε < 1 results in a qualitatively similar change to the total inertia ellipse – the eigenvectors, which determine the ellipse orientation, remain unchanged.
![$$\displaystyle\begin{array}{rcl} M_{rendered}& =& \epsilon \left [\begin{array}{cc} \varDelta a&\varDelta b\\ \varDelta b &\varDelta c\\ \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_12_Chapter_Equ5.gif)
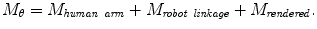
(12.4)
![$$\displaystyle\begin{array}{rcl} M_{rendered}& =& \epsilon \left [\begin{array}{cc} \varDelta a&\varDelta b\\ \varDelta b &\varDelta c\\ \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_12_Chapter_Equ5.gif)
(12.5)
12.2.2 Human Subjects
Patients with damage to the cerebellum but no signs of sensory loss or extracerebellar damage were recruited. The severity of each patient’s cerebellar impairment was determined using the International Cooperative Ataxia Rating Scale (ICARS) [34]. Table 12.1 lists cerebellar subjects ordered by the ICARS kinetic functions subscore, which assesses voluntary limb movements. Scores range from 0 (normal) to 52 (severe). Subject diagnosis is based on medical history, family history, and a neurological examination. The cause of ataxia may be abrupt damage to cerebellar tissue (stroke or trauma), genetic diseases (ADCA, SCA6, and SCA8), or unknown (sporadic) [4]. All subjects gave informed consent to the protocols approved by the Johns Hopkins Medical Institutions Review Board.
Table 12.1
Subject characteristics
Subject | Sex | Dominant hand | Age (years) | Height (m) | Weight (kg) | Diagnosisa | Limb score |
|---|---|---|---|---|---|---|---|
Cerebellar 1 | M | R | 75 | 1.63 | 77 | Stroke | 13/52 |
Cerebellar 2 | F | R | 52 | 1.58 | 51 | Stroke | 15/52 |
Cerebellar 3 | F | R | 20 | 1.68 | 64 | Trauma | 18/52 |
Cerebellar 4 | F | R | 65 | 1.68 | 61 | Sporadic | 18/52 |
Cerebellar 5 | M | L | 37 | 1.78 | 123 | SCA8 | 20/52 |
Cerebellar 6 | M | R | 56 | 1.80 | 90 | SCA6,8 | 23/52 |
Cerebellar 7 | M | L | 57 | 1.70 | 96 | ADCA | 25/52 |
Cerebellar 8 | F | R | 69 | 1.70 | 68 | Sporadic | 23/52 |
12.2.3 Methods of Robot Assistance
The anisotropic nature of arm inertia and other dynamic effects necessitate a non-trivial calculation of the muscle activity needed to reach rapidly in a given direction. It has been hypothesized that the cerebellum plays a key role in planning such movements and that damage to the cerebellum results in a degradation of the ability of the motor control system to plan these movements, accounting for the characteristic misdirection of observed arm movements [5, 6, 21, 22, 26]. The first assistive method explores this possibility in the attempt to derive an optimal, patient-specific assistance method. The second method applies a simple and generic method for assistance. As mentioned in Sect. 12.1, the cerebellum is thought to play a key role in accounting for (adapting to) changes in the dynamics. As such, subsequent to practicing with both of these assistive methods, additional null trials were incorporated into the experimental protocols to search for evidence of adaptation.
12.2.3.1 Assistance Method 1: Dynamics Augmentation
Phase 1: Identifying Optimal Augmentation
In [15], the KINARM robot was used to record the movements of cerebellar patients (Cerebellar 1–8, Table 12.1) performing a targeted reaching task. This task focused on early movement because the role of the cerebellum is most observable during early movement. Subjects made center-out movements through 1 cm diameter targets at a 3 cm radius within a 350–650 ms window. Offline analysis of this data and the arm dynamic model were used to test various hypotheses proposed in the literature about the role of the cerebellum, all of which assume that the cerebellum functions as an internal model of limb dynamics for planning movements. It follows that damage to the cerebellum results in movements that do not properly account for arm dynamics. If this error is known, the potential exists for predicting reaching errors during early movement (before movement feedback is available).
During early movement, arm dynamics can be approximated as (12.6) [14, 15]. The parameters a, b, c, and d are all non-negative scalars, the first three relating to mass properties and the last relating to centripetal and Coriolis forces.
![$$\displaystyle\begin{array}{rcl} \left [\begin{array}{c} \tau _{1}\\ \tau _{ 2}\\ \end{array} \right ]& =& \left [\begin{array}{cc} a&b\\ b &c\\ \end{array} \right ]\left [\begin{array}{c} \ddot{\theta }_{1}\\ \ddot{\theta }_{ 2}\\ \end{array} \right ] + \left [\begin{array}{ccc} 0& - 2d& - d\\ d & 0 & 0 \end{array} \right ]\left [\begin{array}{*{10}c} \dot{\theta }_{1}^{2}\\ \dot{\theta }_{ 1}\dot{\theta }_{2} \\ \dot{\theta }_{2}^{2}\\ \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_12_Chapter_Equ6.gif)
![$$\displaystyle\begin{array}{rcl} \left [\begin{array}{c} \tau _{1}\\ \tau _{ 2}\\ \end{array} \right ]& =& \left [\begin{array}{cc} a&b\\ b &c\\ \end{array} \right ]\left [\begin{array}{c} \ddot{\theta }_{1}\\ \ddot{\theta }_{ 2}\\ \end{array} \right ] + \left [\begin{array}{ccc} 0& - 2d& - d\\ d & 0 & 0 \end{array} \right ]\left [\begin{array}{*{10}c} \dot{\theta }_{1}^{2}\\ \dot{\theta }_{ 1}\dot{\theta }_{2} \\ \dot{\theta }_{2}^{2}\\ \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_12_Chapter_Equ6.gif)
(12.6)
Knowledge of each patient’s arm dynamics allows inverse dynamic calculations to identify torque trajectories to each target. Because of the movements start from rest and are rapid, the magnitude of the acceleration greatly exceeds that of the velocity for the movements recorded. As such, the trajectories are insensitive to variations in d and so the computer simulations searched for a perturbation over the reduced set, {a, b, c}, that when used in forward dynamic simulations with the torque trajectories, optimally reduced reaching errors. Perturbations of this type are equivalent to reshaping and reorienting the arm inertia ellipse [9]. Though no change to arm dynamics was found that fully removed errors, patient-specific perturbations were found that resulted in a reduction in root-mean-squared directional reaching errors of 41 % averaged over 7 cerebellar patients.
Phase 2: Applying Prescribed Augmentation
A subset of these patients were available to return to perform a follow-up experiment to apply the dynamic augmentations predicted to most improve reaches. The KINARM robot was controlled to effectively reshape and/or increase or decrease the arm inertia. Three particular subjects were selected because distinct optimal perturbations were predicted and their ataxia severities spanned those of the group. These perturbations are summarized in Table 12.2 (columns 2–5). It follows that the opposite perturbation (i.e. {Δ a, Δ b, Δ c} vs. 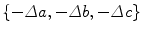 ) would significantly hinder reaching performance, which could be a resistive approach to neurorehabilitation (see Sect. 12.1.2).
) would significantly hinder reaching performance, which could be a resistive approach to neurorehabilitation (see Sect. 12.1.2).
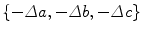 ) would significantly hinder reaching performance, which could be a resistive approach to neurorehabilitation (see Sect. 12.1.2).
) would significantly hinder reaching performance, which could be a resistive approach to neurorehabilitation (see Sect. 12.1.2).Table 12.2
A perturbation predicted to help patients was applied during a reaching task. The predicted optimal change in arm inertia, characterized by ellipse eccentricity, size, and orientation, for each subject is summarized along with the extent to which reaching performance is predicted to improve. The effect of applying the opposite perturbation (e.g. to reduce mass rather than add) was also explored with the goal of resisting rather than assisting movement. The full perturbation could not always be applied for stability reasons. During practice trials, conservatively safe values of ε (12.5) for each patient and for both the perturbation expected to help and hinder performance were determined and are also listed, ε help and ε hinder , respectively
Δ eccentricity | Δ size | Δ orientation | Predicted error | |||
|---|---|---|---|---|---|---|
Subject | (%) | (%) | (deg) | reduction (%) | ε help | ε hinder |
Cerebellar 1 | − 34 | − 61 | 1 | 37.5 | 0.8 | 0.8 |
Cerebellar 5 | − 14 | − 47 | 5 | 62.5 | 1.0 | 0.75 |
Cerebellar 6 | − 39 | − 99 | 2 | 62.9 | 0.3 | 0.3 |
The task in this phase was nearly identical except that the center-out movements were to, not through, targets at a 10 cm, not 3 cm, radius. The more distant spacing of these targets compared to those in the Phase 1 task was chosen to permit investigation of the method’s effect on movement both before and after peripheral feedback can be used. Another subtle difference compared to the preliminary studies is that four, rather than eight, targets were used to obtain a greater number of reaches to each target.
At the beginning of each trial, the subject moved to a center position (shoulder at 35∘, elbow at 90∘). After a slight delay, one of four targets appeared randomly, to which subjects were directed to move within a 200–550 ms time window. Trials were divided into five blocks (Fig. 12.2). Movement duration feedback was given to the subjects in the form of color coding: the target turned blue if reached late, red if early, or green if on time. At the end of each trial, the actual hand path taken was shown to subjects. All trials were analyzed, whether or not the timing criteria were met.
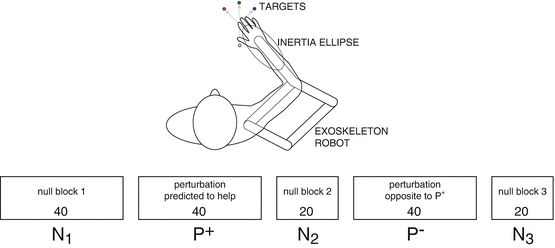
Fig. 12.2
Horizontal reaching task with augmented arm inertia. During the null blocks  , the robot is passive as the patient moves to one of four targets, the blocks containing 40, 20, and 20 trials, respectively. During the first perturbation block P +, the robot augments arm inertia in a manner predicted to help as the subject makes a total of 40 reaches to 4 targets. The second perturbation block P − is identical except the robot augments arm inertia with the opposite sign
, the robot is passive as the patient moves to one of four targets, the blocks containing 40, 20, and 20 trials, respectively. During the first perturbation block P +, the robot augments arm inertia in a manner predicted to help as the subject makes a total of 40 reaches to 4 targets. The second perturbation block P − is identical except the robot augments arm inertia with the opposite sign
 , the robot is passive as the patient moves to one of four targets, the blocks containing 40, 20, and 20 trials, respectively. During the first perturbation block P +, the robot augments arm inertia in a manner predicted to help as the subject makes a total of 40 reaches to 4 targets. The second perturbation block P − is identical except the robot augments arm inertia with the opposite sign
, the robot is passive as the patient moves to one of four targets, the blocks containing 40, 20, and 20 trials, respectively. During the first perturbation block P +, the robot augments arm inertia in a manner predicted to help as the subject makes a total of 40 reaches to 4 targets. The second perturbation block P − is identical except the robot augments arm inertia with the opposite signTo ensure that the robot would remain stable throughout the experiment, the magnitude of the inertia perturbation, ε, was gradually increased towards the desired magnitude while patients practiced the target reaching movements until the onset of instability was detected. This detection was done using digital scopes that report the joint accelerations and motor commands where the onset of instability was evident well before it was perceptible to the subject, resulting in a conservative limit. For the patients tested, the level of perturbation rendered varied from 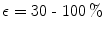 (12.5). Force levels and dynamic perturbations are given in Table 12.2, columns 6 and 7.
(12.5). Force levels and dynamic perturbations are given in Table 12.2, columns 6 and 7.
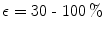 (12.5). Force levels and dynamic perturbations are given in Table 12.2, columns 6 and 7.
(12.5). Force levels and dynamic perturbations are given in Table 12.2, columns 6 and 7.Reaching performance was measured using lateral deviation Δ err of the finger at 150 ms (12.7), where the finger location and target vectors are 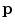 and
and 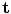 , respectively (Fig. 12.3). It is computed as:
, respectively (Fig. 12.3). It is computed as:
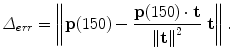
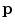 and
and 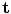 , respectively (Fig. 12.3). It is computed as:
, respectively (Fig. 12.3). It is computed as: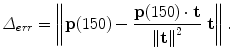
(12.7)
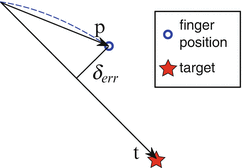
Fig. 12.3
Depiction of error metric: lateral deviation of the finger position from the target path (12.7)
12.2.3.2 Assistance Method 2: Force Channel Rendering
This potential reaching assistance method applies force channels designed to improve reaching performance by enforcing the coordination needed to follow a straight path. Furthermore, these channels are used in an attempt to elicit use-dependent learning, or improvements in both the straightness of the path (lateral error) and the ability to stop at the target (overshoot error) subsequent to channel reaching.
Six cerebellar patients performed this experiment (Cerebellar 2 and 4–8 in Table 12.1). Because it has been reported that use-dependent learning is stronger when the non-dominant arm is trained, that arm was tested whenever possible. The one exception was the case of Cerebellar 6, whose non-dominant arm had a reduced range of motion. Also, Cerebellar 5 was available to have both arms tested.
Force channels were rendered by the KINARM to provide a simple form of assistance during reaching. These channels act as virtual walls to constrain movement by applying a forces perpendicular to the desired direction of movement. The forces are smooth and allow the subject to maintain complete control over the speed of movement. Figure 12.4 illustrates the relationship between finger position, target location, and the spring-like force generated. Given the positions of the finger, 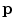 , and target,
, and target, 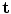 , the channel force with stiffness k c in Cartesian space is given by:
, the channel force with stiffness k c in Cartesian space is given by:
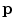 , and target,
, and target, 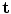 , the channel force with stiffness k c in Cartesian space is given by:
, the channel force with stiffness k c in Cartesian space is given by: