Fig. 1
Schematic illustration of the sensor fusion mechanisms. Information of sensory transducer signals is fused in the first step to yield physical variables. These variables are used in the second step to reconstruct external disturbances
2.1.1 Fusion of Sensory Transducer Data
An example of the first step is the human sense of joint angle proprioception. It combines information from several sensory transducers such as muscle spindles, Golgi tendon organs and cutaneous receptors [36]. This also applies to the human perception of head on trunk rotation, which in addition is complicated by the fact that rotations between several segments of the cervical vertebral column are involved. Yet, the result is a sense of angular head-on-trunk velocity and position, as if an angular rate sensor and a goniometer in a single joint were measuring head-trunk speed and rotation, respectively [37, 38].
Another example for the first step, well known to engineers who work with IMUs, is the fusion of angular and linear accelerometer signals. A problem with linear accelerometers is that they do not distinguish between inertial and gravitational forces (i.e. between linear acceleration and tilt of the sensor). There exists also a problem with the angular accelerometers, often used in the form of gyros that measure angular velocity. They show low frequency signal variations over time (‘drifts’). Both problems can be solved for the earth vertical planes by fusing the inputs from the two sensors in an appropriate way. This has an analogy in the human vestibular system that is located in the inner ears. Its otolith organs and canal systems represent biological equivalents of linear and angular accelerometers, respectively [39]. The solutions for both, the technical system and its biological equivalent involve information of the gravitational vector. In the horizontal translational and rotational planes, however, there is no such information available, so that further sources of information are required. In technical systems, often the GPS is used. Humans usually use the visual system for this purpose.
In the following we will speak of joint angle and angular velocity sensors and by this we mean virtual sensors that result from step one. The same applies when we refer to the vestibular sensor and its three output measures, i.e. 3D angular velocity and linear acceleration in space and 2D orientation with respect to the gravitational vertical. These measures of the physical variables represent the inputs to the second step of the sensor fusions.
2.1.2 Disturbance Estimation
In the second step of Fig. 1, the signals of the variables resulting from step one are combined to reconstruct external disturbances that have impact on the body. In the DEC concept, it is assumed that four physical quantities suffice to define the external disturbances that affect human balancing in moderate stimulus conditions (body sway amplitudes and velocities, <8° and <80°/s; frequencies, <3 Hz). The four types of external disturbances are: (1) Support surface rotation, (2) support surface translational acceleration, (3) field forces such as gravity, and (4) contact forces such as a pull on, or push against the body.
The second step in Fig. 1 was originally motivated by reports of the subjects in the aforementioned psychophysical experiments. When asked to report their percepts during passive rotations on a rotation chair, subjects typically started the report with the rotation of the chair, even though the percept primarily stems from the vestibular system in the head. Thus, without being aware of it, the subjects reconstructed the physical cause of their body rotation, i.e. the chair rotation in space, by internally reversing the linkages from the vestibular signal ‘head rotation in space’ via the proprioceptive signal ‘trunk rotation relative to the head’ to the haptical information of ‘sitting on the chair’. This can formally be described in terms of a transformation by which the trunk and chair kinematics are referenced to the vestibular derived notion of inertial space [25]. The concept applies to both, the vestibular-able subjects’ estimation of ‘support rotation’ and ‘support translational acceleration’ in Fig. 1 (formal description in Sect. 2.2).
Vestibular-able subjects furthermore use vestibular information for estimating body lean with respect to the earth vertical when balancing stance in the sagittal plane. From lean of the whole-body’s center of mass (COM B ) above the ankle joints and knowledge about body mass and COM height they to estimate the required ankle joint torque to compensate for the gravity effect. For field forces in general, it is known that subjects, when presented with a new aspect of a field force, they perceive it and readily learn to counteract its impact on the body. Thereafter, they no longer perceive it consciously, as has been shown in Coriolis force experiments by Lackner and DiZio [27]. The subconscious estimation and compensation of field forces makes it difficult to study them psychophysically.
Estimation of contact force effects on the ankle joint balancing requires internal measurement of the overall ankle torque (or related measures such as the center of pressure, COP, shift) and the distinct contributions to the ankle torque such as active torque and the gravitational torque. Details have been described before [40] for sagittal plane balancing of moderate disturbances, where the balancing is performed predominantly in the ankle joints (‘ankle strategy’; [41, 42]). In such situations, a single inverted pendulum, SIP, can approximately mimic human biomechanics.
2.1.3 Feedback Control Model
The two steps of sensor fusion are used for feedback control of one joint (Fig. 2). Its lower half represents a servo control consisting of a negative joint angle proprioceptive feedback and a controller with a proportional and a derivative factor (PD controller). The controller provides the motor command that is transformed by the muscles into joint torque (not shown in Fig. 2). Given appropriate parameters of the servo control, actual joint angle approximately equals the desired joint angle without requiring a feed forward of plant dynamics. Feedback from passive stiffness and viscosity with virtual zero delay is assumed to amount to 10 % of the proprioceptive feedback (not shown in Fig. 2).
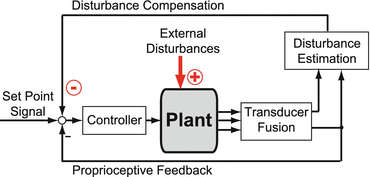

Fig. 2
Simplified feedback control scheme of the Disturbance Estimation and Compensation (DEC) concept. The Proprioceptive Feedback loop yields a servo control, by which actual joint angle approximately equals the desired joint angle. Signals from the Disturbance Estimation part command the servo to compensate the disturbances
Noticeably, in the SIP scenario, the P and D factors identified in human stance control are surprisingly low [10, 14, 43]. They appear to be geared to the pendulum mass m, the height h of the COM, and gravitational acceleration g (mgh; P ≈ mgh; D ≈ mgh/4). The values that humans use for balancing are only slightly higher. A consequence is that the servo alone is insufficient to cope with external disturbances such as gravity or a push against the body.
The upper half of Fig. 2 shows schematically the loop that carries the estimates of the external disturbances and compensates for them. To insure control stability in face of the neural time delays, the field and contact force estimates are not used directly, but in the form of body-space angle equivalents. For example, the estimate of body lean commands the servo to compensate for the gravitational torque it produces. Then, the loop gain (at the level of the controller) is raised accordingly. Noticeably, the increase occurs only at the time of, and to the extent that the disturbance has impact. Note furthermore that disturbance compensation applies even with superposition of several disturbances as well as with superposition of disturbances and voluntary movements [39].
The DEC loops are not simply representing additional sensory feedback loops, but are thought to represent long-latency loops through basal ganglia and cerebral cortex [40]. They contain central detection thresholds and allow for voluntary scaling the disturbance compensations and for predictions of the disturbance estimates (e.g. self-produced disturbances during voluntary movements).
It has been shown by comparing human data with model simulations that the DEC concept describes the human ankle joint balancing in a variety of disturbance scenarios. Furthermore, the control automatically adapts to changes in disturbance scenario and magnitude as well as sensor availability. This also applied when the model was implemented in a humanoid robot with ankle joint actuation, and tested in the human experimental setup (PostuRob I; overview [39, 40]). These experiments demonstrated that the DEC concept is robust against real world problems such as inaccurate and noisy sensors and mechanical dead zones.
The following describes an extension of the DEC concept to include the hip joints in the balancing. The hip joints contribute considerably when strong transient disturbances are applied (‘hip strategy’; [41, 42]). Then humans may use hip joint accelerations to produce shear forces under the feet to counteract body COM excursions. Another, more common involvement of the hip joints deals with adding to the task of body COM balancing a secondary task of keeping the orientation of the upper body upright. This ‘head stabilization in space’ task is thought to improve under dynamic conditions such as walking the sensory feedback from the vestibular and visual cues arising in the head [44, 45].
2.2 Extended DEC Concept: Sensor Fusion in Ankle and Hip Joint
The extension of the DEC concept for including the hip joints entails that double inverted pendulum (DIP) rather than SIP biomechanics are considered, and with this the occurrence of inter-segmental coupling torques [46]. In an extended DEC concept for DIP biomechanics, we postulated two DEC controls, one for the hip joint and the other for the ankle joint. This approach allowed to use again the above described sensor fusion principles for disturbance estimation.
2.2.1 DIP Biomechanics
The DIP biomechanical model is shown in Fig. 3. In Fig. 3a, COM T , COM L and COM B stand for the COM of the trunk (including head and arms), leg and whole body, respectively. Leg length is given by l L , the trunk and leg COM heights are given by h T and h L , respectively. Figure 3b shows the angular excursion of the trunk and leg segments with respect to earth vertical (trunk-space angle α TS , leg-space angle α LS ). Angular excursion of COM B is defined as body-space angle α BS . The foot has firm contact with the support surface, therefore platform tilt angle equals foot angle with respect to earth horizontal (foot-space angle α FS ). The trunk-leg joint angle is α TL and the leg-foot joint angle is α LF . In perfectly upright body position, all angles are 0°. Angular speed during reactive human balancing can be assumed to be slow enough such that the Coriolis and centrifugal forces can be neglected; the model can be linearized using small angle approximation, assuming that the subject is maintaining his upright position close to the vertical.
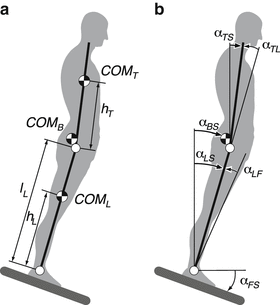

Fig. 3
DIP biomechanics
Maintaining upright stance in the situation of a support surface tilt in the sagittal plane requires corrective joint torque in the ankle and hip joints. This torque can be expressed by the following equations for hip torque T H
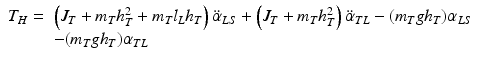
and for ankle torque T A
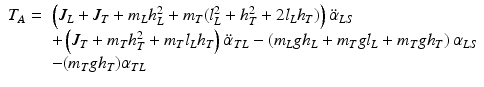
where 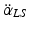 , and
, and 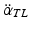 represent angular accelerations, m L and m T are the segment masses, and J L and J T the segment moments of inertia (details in Al Bakri [47]).
represent angular accelerations, m L and m T are the segment masses, and J L and J T the segment moments of inertia (details in Al Bakri [47]).
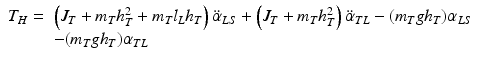
(1)
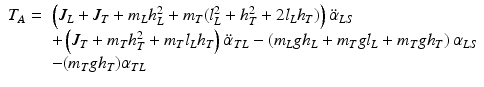
(2)
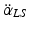 , and
, and 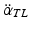 represent angular accelerations, m L and m T are the segment masses, and J L and J T the segment moments of inertia (details in Al Bakri [47]).
represent angular accelerations, m L and m T are the segment masses, and J L and J T the segment moments of inertia (details in Al Bakri [47]).In the extended DEC concept for the DIP, the hip joint is used for orienting and balancing the trunk segment and the ankle joint for balancing the whole-body using two separate controls. The vestibular-derived signals used for the controls are: the trunk-space angle α ts , trunk-space angular velocity 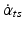 , and head translational acceleration
, and head translational acceleration 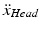 . The proprioceptive signals are: the trunk-leg angle α tl and the trunk-leg angular velocity
. The proprioceptive signals are: the trunk-leg angle α tl and the trunk-leg angular velocity 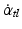 ; the leg-foot angle α lf and the leg-foot angular velocity
; the leg-foot angle α lf and the leg-foot angular velocity 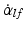 . Uppercase letters in the angle subscripts indicate physical angles, lowercase letters the sensory derived representations of these angles.
. Uppercase letters in the angle subscripts indicate physical angles, lowercase letters the sensory derived representations of these angles.
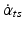 , and head translational acceleration
, and head translational acceleration 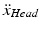 . The proprioceptive signals are: the trunk-leg angle α tl and the trunk-leg angular velocity
. The proprioceptive signals are: the trunk-leg angle α tl and the trunk-leg angular velocity 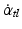 ; the leg-foot angle α lf and the leg-foot angular velocity
; the leg-foot angle α lf and the leg-foot angular velocity 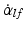 . Uppercase letters in the angle subscripts indicate physical angles, lowercase letters the sensory derived representations of these angles.
. Uppercase letters in the angle subscripts indicate physical angles, lowercase letters the sensory derived representations of these angles.2.2.2 Hip Joint Control
The DEC control of the trunk reflects the principles described already above for the SIP biomechanics. Considering the support surface tilt scenario in the sagittal plane shown in Fig. 3, the legs tend to rotate somewhat with the platform, due to passive ankle joint stiffness and a imperfect tilt compensation that is typical in humans with eyes closed. Since the legs represent the support base for the trunk, an eccentric hip rotation represents:
(a)
A support base tilt disturbance for the trunk, evoked by the leg rotation, α LS .
(b)
A hip translational acceleration 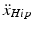 . It produces a hip torque (T H_in ) in relation to m T , h T and J T . This torque is treated here as if it were an external disturbance rather than an inter-segmental coupling effect.
. It produces a hip torque (T H_in ) in relation to m T , h T and J T . This torque is treated here as if it were an external disturbance rather than an inter-segmental coupling effect.
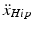 . It produces a hip torque (T H_in ) in relation to m T , h T and J T . This torque is treated here as if it were an external disturbance rather than an inter-segmental coupling effect.
. It produces a hip torque (T H_in ) in relation to m T , h T and J T . This torque is treated here as if it were an external disturbance rather than an inter-segmental coupling effect.Furthermore, trunk lean is associated with a gravitational hip torque disturbance (T H_grav ).
These three disturbances are estimated in the DEC control of the hip joint control in the following form:
(i)




Estimation of leg tilt, 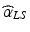 . This estimate is derived from fusing the vestibular velocity signal
. This estimate is derived from fusing the vestibular velocity signal 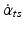 with the proprioceptive velocity signal
with the proprioceptive velocity signal 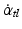 by
by 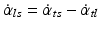 (Assumption: these transformations are performed as vector summations of co-planar rotations, separately for the three body planes).
(Assumption: these transformations are performed as vector summations of co-planar rotations, separately for the three body planes). 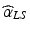 is obtained by applying to the signal a detection threshold and a mathematical integration.
is obtained by applying to the signal a detection threshold and a mathematical integration.
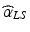 . This estimate is derived from fusing the vestibular velocity signal
. This estimate is derived from fusing the vestibular velocity signal 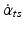 with the proprioceptive velocity signal
with the proprioceptive velocity signal 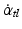 by
by 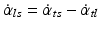 (Assumption: these transformations are performed as vector summations of co-planar rotations, separately for the three body planes).
(Assumption: these transformations are performed as vector summations of co-planar rotations, separately for the three body planes).  is obtained by applying to the signal a detection threshold and a mathematical integration.
is obtained by applying to the signal a detection threshold and a mathematical integration.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree







