11 Microelectrode recording of deep brain structures was introduced in the early 1960s by the French neurophysiologist Albe-Fesard. This technique rapidly gained wide popularity initially among researchers, later with a few neurologists and neurosurgeons involved in functional neurosurgery. Microelectrode technique had a second birth among clinicians with the resurgence of surgical treatment of essential tremor and Parkinson’s disease (thalamotomy thalamic stimulation, pallidotomy, pallidal stimulation, and subthalamic stimulation). MER was used to help the surgical team to refine the target. The scope of this chapter is directed mainly toward the clinical use of data processing and pattern recognition for microelectrode recording in humans. Native signals derived from MER cannot be processed directly in either analog or digital form; instead, they must be preprocessed to allow further treatment. Microneurographic signal processing consists of several steps. First, the signal derived from MER must be amplified to a suitable level for further processing using an amplifier with a gain generally ranging from 1000 to 10,000. The goal is to keep the signal-to-noise ratio as high as possible. The signal is then filtered. Signal output may be observed on an oscilloscope, an audio monitor, or other devices for online monitoring. The microrecording signal also should be digitized at an optimal sampling rate using an analog-to-digital (A/D) converter to allow computer storage and analysis (in real time or off-line). The signal eventually may be archived either analogically or digitally for off-line analysis and data sharing with other teams. Signals obtained from microelectrode recordings can be categorized as background noise or neuronal discharges (spikes). Neuronal discharges can be characterized using three main parameters, depending on the type of neuronal activity: tonic activity (firing rate), phasic activity (spike pattern), and stimulus-induced activity (delay and pattern). Precise characterization of neuronal activity potentially serves many objectives: recognition (or confirmation) of the structure targeted, understanding of the local physiology or pathophysiology, and sharing information with other teams. Commercially available equipment exists to perform either the full process, including amplification and data processing (e.g., Guideline System 3000, Axon Instruments; Website: www.axon.com), or only part of it. Neurophysiological software is also available commercially or as freeware/shareware on the Internet. Among the commercially available software, the following products are often cited in the neurosurgical literature: Spike-2 (Cambridge Electronic Design),1 LabView (National Instruments; Web site: www.lab-view.com), DataPac2000 (Run Technologies; Website: www.runtech.com), pClamp8 (Axon Instruments), and DataView (University of St. Andrews; Web site: biology.st-and.uk/sites/dataview). We developed our own neurophysiological software called InterSpike using Delphi (Inprise-Borland) and decided to make it available on the Web as shareware (www.interspike.ch). Hundreds of software modules are currently available for sound processing and filtering, so it is impossible to list them all. The goal of amplification is to transform the amplitude of the electrical signal derived from MER (typically < 1 mV) into an electrical signal usable by output devices such as an audio monitor or a computer interface digitization device (such devices require input signal amplitudes in the range of volts). The key issue with amplification is to keep the signal-to-noise ratio as high as possible. The single-unit activity (action potential discharge) is generally amplified by a factor of 10001 to 10,000X.2,3 A good strategy for amplification may be to split the gain and have the signal filtered in between the amplification stages (see below). For example, an initial gain of 1000X (or 100X) followed by low-pass filtering and amplification by 10 (or 100) will usually give better results than a direct amplification using 10,000X gain because proper filtering helps to avoid signal distortion due to amplifier saturation by the high-frequency components of noise. Various commercially available neurophysiology-oriented amplifiers can be used for this purpose.1–4 In the operating room, the signal derived from an MER recording is easily distorted by various electrical activities (stray electrical noise). Filtering is definitely one of the key issues that need close attention to achieve good results. Filtering can be applied directly to the native analog signal using electronic filters, or it can be performed after digitization with the help of mathematical algorithms. Which approach is better? Analog filters are inexpensive, fast, and offer a large dynamic range in both amplitude and frequency. However, analog filters have physical limitations that restrict the achievable transfer characteristics. Digital filters, by comparison, offer a vastly superior level of performance that can be achieved. Digital filters work so well that the performance of the filter can be ignored, and the emphasis instead shifts to the limitations of the signal and the theoretical issues regarding signal processing.5 The bandwidths commonly used for human brain microrecording are 300 Hz to 10 kHz2,6 or 600 Hz to 6 kHz.3 Band-pass filtering of this type is achieved by combining a low-pass and a high-pass filter. With regard to signal transfer characteristics, there are several types of filters available. The Bessel filter, also called a “linear-phase” or “constant delay” filter, is one that is appropriate for pulselike signals such as neuronal spikes. This is a low-pass filter that alters the phase of the sinusoidal component of the signal linearly with respect to the frequency. The Bessel filter is used, for example, in the CyberAmp series of amplifiers (Axon Instruments). This type of filter introduces a smaller artifact (overshoot) after an input step than many other low-pass filters with other characteristics (such as the Butterworth filter). One commonly encountered perturbation that may require filtering is the 60 Hz (United States) or 50 Hz (Europe) noise signal caused by proximity of the general electrical supply to the microelectrode recording. A notch filter can be used to reduce this interference. The notch filter will decrease the gain of the amplifier to a very low value at this specific frequency but keeps normal gain values for neighboring frequencies. Because some components of the sought-after neural signal may be at 50 or 60 Hz, the notch filter should be used judiciously on the native signal. In every case a serious effort should be made to reduce the 50 or 60 Hz interference by other means (e.g., by turning off the power to the offending instrument, appliance, overhead lights, or patient’s bed). One strategy to detect potential distortion of the signal with notch filtering is to store the native signal, then apply a digital noise filter. This will allow comparison of both filtered and unfiltered signals, permitting the user to choose the best compromise. Though very helpful, filtering is such a complex issue that it goes far beyond the scope of this chapter. It is impossible to describe all the potential techniques (analog or digital) that can be used in neurophysiology.7 Interested readers should refer to the manual of the amplifier they use as well as to specific literature on filtering technologies. Two main parameters define the digitization process: sampling rate and resolution. An inexpensive and effective way to digitize the microelectrode signal is to use a computer sound card. Careful selection of a quality card is important. The signal to noise ratio can be extremely different, even for two sound cards with the same brand name. We strongly recommend that the user establish this ratio using a signal generator prior to using the sound card in a neurophysiological application. Many computer sound cards offer two levels of resolution: 8 or 16 bits (full scale). For both spike detection and background noise analysis, the 16-bit depth gives better results than the 8-bit resolution. Voltage encoding using 16 bits provides granularity of 65,536 amplitude steps. As with all digital signal-processing instruments, there is one potential pitfall to keep in mind concerning the correct sampling rate. If there is any component present in the incoming signal that has a period that is less than twice the sampling interval, then the signal component will falsely appear in the frequency analysis as a component of much lower frequency8 This effect is called “aliasing.” Such distortion of the signal is analogous to the visual illusion encountered in old western movies in which the wheels of a rapidly moving stagecoach appear to rotate backward (because the movie frames were not shot rapidly enough). “Aliasing” can be avoided by proper (lower) setting of the low-pass filter or by increasing the sampling rate. Most sound cards offer three sampling rates: 11, 22, and 44 kHz. We found the 22 kHz sampling rate to be optimal for action potential (spike) detection in the globus pallidus. The 44 kHz sampling rate was slightly superior for the analysis of summed activity (background noise). In the subthalamic nucleus (where neurons are closely packed together), it is better to use the 44 kHz sampling rate. The higher sampling rate eases the detection of non-single-cell recording by providing a higher dynamic range. In addition to the possibility of post hoc data filtering and analysis, one major advantage that is provided by digitization of the microelectrode recording signal is the ease of permanent archival storage of the data and sharing of the (raw) information with other teams. The amount of raw data, however, can be staggering. For a 44 kHz sampling rate and 16-bit digitization depth (2 bytes on a personal computer), each second of electrophysiological recording results in 88 kbytes of data. One minute of microrecording will therefore occupy roughly 5 megabytes (5280 kbytes). Consequently, one CD-ROM (650 megabytes) will be required for every 2 hours of microrecording data (assuming only one recording channel is used). Common sound cards have two input channels and can therefore digitize simultaneously two separate signals, such as microrecording or surface EMG. When more than two signals need to be recorded simultaneously, a special sound card (with up to eight input channels) or a dedicated digitizing unit must be purchased. Conceptually, neural “noise” (not to be confused with instrumental noise) is fundamentally different from spike activity of individual neurons. Spikes are discrete discontinuous events occurring at particular points in time, whereas neural noise appears more like a continuous analog signal modulated over time. In 1977, Fukamachi et al described a quantitative method to analyze the neural noise within the human thalamus.9 Because of the lack of computer power, the authors used an averaging circuit. The output signal from the amplifier was first filtered by a high-pass filter with a 50 Hz or 100 Hz cut-off frequency. The signal was then rectified and integrated to give a continuous averaged amplitude of the neural noise. This averaged amplitude was then continuously displayed and plotted throughout the trajectory of the electrode. Although this technique of analyzing neural activity may seem rather crude, it was helpful for differentiating the white matter from the thalamus and the caudate nucleus during surgical procedures. Many parameters affect the neural noise.10 One parameter determinant in the generation of the neural noise is the nearby spiking activity, but the local impedance of the tissue that varies from one structure to the other11 will change the recorded neural noise. Noise analysis can be nicely performed using a “continuous” fast Fourier transform (FFT) over time. Yoshida applied this technique to the neural noise measured with semimicroelectrodes in human subcortical structures during thalamotomy12 The FFT analysis provided convincing differentiation of the white matter, caudate nucleus, dorsal thalamus, Vim, and field of Forel. Taha et al used a similar technique to study the functional anatomy of the pallidal base in Parkinson’s disease.13 In three quarters of the patients, the neural noise at the base of the globus pallidum showed a sharp transition when the microelectrode tip was entering in the ansa lenticularis, but in a quarter of the patients there were multiple successive transitions in the neural noise level over a distance of 0.4 to 2 mm (median = 1 mm). In practice, the background (neural) noise analysis is done by running an FFT transform on one short-time segment of the signal at a time. The transform results can be plotted as a three-dimensional or two-dimensional plot. When a three-dimensional representation is used, time is plotted on one axis (typically in units of seconds), the amplitude of the spectrum (arbitrary unit) is plotted along another axis, and a corresponding frequency of the spectrum (Hz) is plotted along the third axis. When a two-dimensional representation of the transform evolution is used, one axis is the evolved time(s), and the other axis represents the frequency (Hz). The amplitude of the spectrum is color-encoded. Figure 11–1 illustrates the transition in the characteristics of neural noise between the bottom of the GPi and the ansa lenticularis using a two-dimensional, color-encoded FFT plot. Because of the short duration of the action potential, most of the spike activity is filtered by the Fourier transform. It is possible to improve the FFT analysis of neural noise by a two-pass preprocessing procedure consisting of (1) detecting spikes and creating an average spike and (2) subtracting the average spike from the original signal at every occurrence. The simplest way to detect a spike is to use a fixed threshold discrimination device or algorithm. This technique assumes that every time the signal exceeds the threshold it is because of the presence of a spike. This assumption obviously fails in the presence of significant artifacts in the recorded signal. The threshold technique will give reliable results only in the absence of artifacts when the mean level of the signal remains stable. Figure 11–1 Fast Fourrier transform over time representation of the transition from the globus pallidus internalis (Gpi, left) to the ansa lenticularis (right). The microelectrode was advanced with a hydraulic microdrive at an average speed of 50 μ/s. The x-axis represents the time in seconds, which corresponds roughly to the depth. The y-axis represents the frequency in kilohertz, and the power of the spectrum is color-encoded. This drawing is a black-and-white conversion of the original colored representation. For well-behaved signals, automatic threshold determination can be done after establishing the minimal and maximal values of the signal for the entire recording or for a given sample. Usually, it is possible to reduce the negative influence of brief artifacts by eliminating the highest 5% values and the lowest 5% values within the signal from consideration. Another issue arises when using the threshold technique: depending on the sampling rate, a spike may generate many sample values that are above the threshold for spike discrimination. One way to account for this would be to wait until the values of the signal go down to the threshold again before a new spike is regarded as detected. This would be a good technique in the total absence of noise, but in reality, especially when using a high sampling rate, the threshold level can be crossed in both directions several times by a single spike because of the superimposed neural and electronic noise. For this reason, it is more practical to utilize the concept of a refractory period: after the first cut of the threshold that triggers spike detection, the detection routine is disabled for a short period of time (a few milliseconds) that corresponds to the known minimum refractory period for spike discharge. When spikes from multiple neurons are recorded simultaneously (rather than spikes from a single active neuron), the threshold algorithm may still work properly, provided that the neurons produce action potentials of different amplitudes and the trigger level is adjusted appropriately (e.g., to ignore the neuron-producing action potential with the smaller amplitude). Sometimes it can be difficult to detect that the signal contains the activity of more than one neuron. One way of solving this issue is to plot recurrently the signal before (Δ time 1) and after (Δ time 2) each threshold detection. When a single neuron is recorded, the morphologies of the superimposed curves are very similar. When two neurons are recorded, the superimposed curves create two separate morphologies. To achieve good results, it is better to apply this technique to a short duration of the signal with ~10 to 50 spikes. More sophisticated methods for spike discrimination (e.g., those relying on principal component analysis of the action potential shape) are available commercially. The average firing rate of a neuron is obviously the easiest parameter to compute and therefore is almost always reported for microelectrode recordings in both animal and human studies.14–17 Tonic activity can be quite constant for a given cell. Spontaneous variations do occur. When the underlying process generating the signal is changing its characteristics over time, it is called “nonstationary” Average rate is a representative measure of the discharge rate, provided that the signal is stationary. Another type of nonstationarity can be observed in microelectrode recordings when the physical characteristics of the microelectrode are slowly changing over time (oxidation, heating, adjacent bleeding). It is possible to correct for this type of nonstationarity by computing the average value of the spike signal in short sections of the recording and finding a function linking the mean value of the signal for each section (e.g., using a cubic-spline extrapolation between these points) and applying the given correction to each single value of the signal. By measuring interspike intervals, it is possible to determine the frequency of discharge. With these values, the mean, median, quartile (p25 and p75), and extreme (p10 and p90) frequencies can be calculated. The mean frequency of discharge is probably the most common reported parameter of single-cell activity.18,19 It can be very helpful for detecting changes in behavior of a given cell subjected to various experimental conditions; however, it is only a rough parameter for comparing the activity of multiple neurons located in various locations. Within a given location the average frequency of discharge can also be very different from one cell to another. Favre et al compared 152 neurons located in the globus pallidus externals (GPe) and 204 neurons located in the globus pallidus internalis in parkinsonian patients.2 They found that firing rates of GPe cells ranged from 11 to 108 Hz, and firing rates of GPi cells ranged from 42 to 201 Hz. Although the firing frequency itself was not characteristic of either the GPe or the GPi, it was still a useful clue because 50% of the GPe cells had a mean frequency below or equal to 42 Hz, which was the lower limit of activity of GPi cells. On the other end of the distribution, half of the GPi cells discharged at frequencies equal to or above 77 Hz; less then 5% of the GPe cells did so. Only 20% of the GPi neurons had mean firing frequency above the upper limit of activity of the GPe cells.
Signal Processing and Pattern Recognition in Microelectrode Recordings
JACQUES FARVE AND THOMAS BAUMANN
Signal Processing
Amplification
Filtering
Digitization
Noise Analysis
Spike Detection
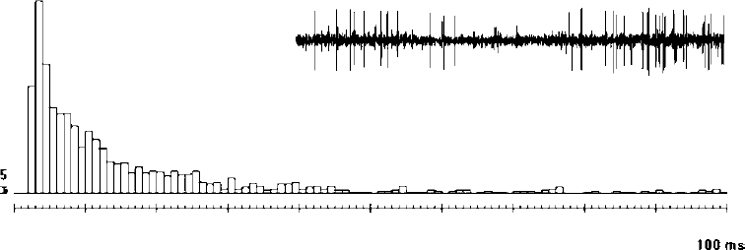
Tonic Activity
Descriptive Analysis
| Author | Gpi | Gpe |
| Favre et al (1999)2 | 42–201 | 11–108 |
| Lozano et al (1998)1 | 60–300 | 10–60 |
| Sterio et al (1994)6 | 58.5 ± 6.3 | 43.5 ± 9.1 |
Table 11-1 summarizes the discharge rates reported by some authors for GPi and GPe neurons in the literature. This table illustrates the intra- and interobserver variations that can be seen and the limitation of the firing frequency value as a characteristic parameter for a given brain region.
Interspike Interval Histogram
Interspike interval histograms describe the frequency distribution of time intervals between two successive spikes. The preferred frequencies of discharge are well illustrated with interspike interval histograms. The quality of the histogram obviously depends on the number of interspike intervals recorded, and the bin width (upper and lower limits of the interspike interval for a given column) should be chosen according to the number of interspike intervals observed. Figure 11–2 illustrates an interspike interval histogram of a typical GPe cell that was calculated for a 25.4 sec recording time, including 1356 spikes. The median interspike interval was 10 ms (upper quartile: 20 ms; lower quartile: 5 ms; p10: 4 ms; p90: 38 ms).
Interspike interval histograms can be compared for clustering purposes (to identify the types of discharges). We used a 10-category interspike interval histogram for each confronted cell. The values for each column were used in a 10 × 2 table, and a chi-square calculation was made. In such a comparison, similarly behaving neurons will result in a “nonsignificant” chi-square value, whereas different neurons would result in a “significant” chi-square value. Figure 11–3 illustrates the comparison of two GPe cells recorded in different patients using the interspike interval histogram comparison method. The resulting chi-square value confirmed the behavior of the two cells to be similar.
Joint-Interval Plots
The pattern of action potential discharge can also be summarized by means of joint-interval histograms. Joint-interval plots are generally represented by scattered-point diagrams.20 Each pair of adjacent interspike intervals is plotted as a point, with one interspike interval as the x-axis value and the next interspike interval as the y-axis value. If the durations of successive interspike intervals are independent values, then the scattered joint-interval diagram will show symmetry along the diagonal (y = x) line.
Related posts:
History of Electrophysiological Recording for Functional Neurosurgery
Programming for DBS Using MER Data
The Future of Microelectrode Recording
Principles of Extracellular Single-Unit Recording
Correlation between Microelectrode Recording and Clinical Effects of High-Frequency Stimulation of the Subthalamic Nucleus
Target Selection Using Microelectrode Recording
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
