the Genesis of Components in the Networks of Interacting Units

(1)

One may view the transition probability as a function of a state variable x and its time derivative x’, that is,

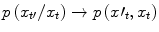
$p\left({x}_{t\prime }/{x}_t\right)\to p\left(x{\prime}_t,{x}_t\right)$

(2)

The dynamical systems law is written by

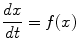
$\frac{dx}{dt}=f(x)$

(3)

Then, one has the following formula.

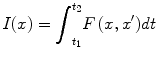
$I(x)={\displaystyle {\int}_{t_1}^{t_2}F\left(x,x^{\prime}\right)} dt$

(4)

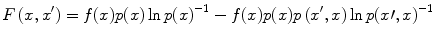
$F\left(x,x^{\prime}\right)=f(x)p(x) \ln p{(x)}^{-1}-f(x)p(x)p\left(x^{\prime },x\right) \ln p{\left(x\prime, x\right)}^{-1}$

(5)

The first and the second terms on the right hand side of Eq. 5 may correspond to the potential energy-like and the kinetic energy-like terms, respectively.

Here, –F(x, x′) is a Lagrangean-like function, which implies local information flow in the present case. Therefore, the ‘variational’ principle is provided by the following formula.

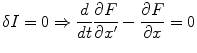
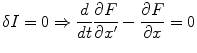
$\delta I=0\Rightarrow \frac{d}{dt}\frac{\partial F}{\partial x^{\prime }}-\frac{\partial F}{\partial x}=0$

(6)

3 Results

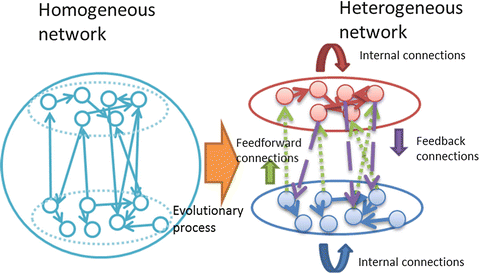
We report the results of the simulations for the genesis of heterogeneously interacting modules from homogeneously interacting modules and the results for the genesis of a neuronal unit. For the former model [3], we found the development of heterogeneous interactions between presumed modules that consist of homogeneous interactions among units (Fig. 1). The development of the dynamics was obtained under the constraint of maximum transmission of information measured by the product of transfer entropies from module I to II and module II to I. We used the networks of the Weyl transformations with noise, which are coupled randomly via sinusoidal transformations of those variables. Using the genetic algorithm, the networks developed from homogeneous couplings to heterogeneous couplings. We observed the following spontaneous symmetry breaking: In one module, say module I, in-phase couplings were dominant, but other types of couplings also survived. In the other module (module II), only in-phase couplings survived. The couplings from module I to II developed to become in-phase couplings only, while those from module II to I developed to become anti-phase couplings only.