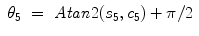Fig. 15.1
The upper limb exoskeleton EXO-UL7 with seven DOFs, supporting 99 % of the range of motion required to preform daily activities
15.2 An Upper Limb Exoskeleton: EXO-UL7
15.2.1 System Overview
The kinematics and dynamics of the human arm during activities of daily living (ADL) have been studied to determine specifications for exoskeleton design (see Fig. 15.1). Articulation of the exoskeleton is achieved by seven single-axis revolute joints which support 99 % of the range of motion required to perform daily activities. Three revolute joints are responsible for shoulder abduction-adduction, flexion-extension and internal-external rotation. A single rotational joint is employed at the elbow, creating elbow flexion-extension. Finally, the lower arm and hand are connected by a three-axis spherical joint resulting in wrist pronation-supination, flexion-extension, and radial-ulnar deviation. As a human-machine interface (HMI), four six-axis force/torque sensors (ATI Industrial Automation, model-Mini40) are attached to the upper arm, the lower arm, the hand and the tip of the exoskeleton. The force/torque sensor at the tip of the exoskeleton allows measurements of the interactions between the exoskeleton and the environment [8, 9, 21].
15.2.2 Kinematic Design of the Upper Limb Exoskeleton EXO-UL7
15.2.2.1 Kinematic Modeling of the Human Arm
The upper limb exoskeleton EXO-UL7 is designed to be compatible with the human arm kinematics. The human arm is composed of segments linked by articulations with multiple degrees of freedom. It is a complex structure that is made up of both rigid bone and soft tissue.Although much of the complexity of the soft tissue is difficult to model, the overall arm movement can be represented by a much rigid body model composed of rigid links connected by joints. Three rigid segments, consisting of the upper arm, lower arm and hand, connected by frictionless joints, make up the simplified model of the human arm. The upper arm and torso are rigidly attached by a ball and socket joint. This joint enables shoulder abduction-adduction (abd-add), shoulder flexion-extension (flx-ext) and shoulder internal-external (int-ext) rotation. The upper and lower arm segments are attached by a single rotational joint at the elbow, creating elbow flx-ext. Finally, the lower arm and hand are connected by a 3-axis spherical joint resulting in pronation-supination (pron-sup), wrist flx-ext, and wrist radial-ulnar (rad-uln) deviation. Models of the human arm with seven DOFs have been widely used in various applications, including rendering human arm movements by computer graphics [22, 23], controlling redundant robots [24, 25], kinematic design of the upper limb exoskeletons [18, 26, 27], and biomechanics [28–30]. These models provide a synthesis of proper representation of the human and the exoskeleton arm as redundant mechanisms along with and adequate level of complexity.
The kinematics and dynamics of the human arm during activities of daily living (ADL) were studied in part to determine engineering specifications for the exoskeleton design [8]. Using these specification, two exoskeletons were developed, each with seven DOFs. Each exoskeleton arm is actuated by seven DC brushed motors (Maxon) that transmit the appropriate torque to each joint utilizing a cable-based transmission. The mechanisms are attached to a frame mounted on the wall, which allows both height and distance between the arms to be adjusted. Articulation of the exoskeleton is achieved about seven single axis revolute joints – one for each shoulder abd-add, shoulder flx-ext, shoulder int-ext rotation, elbow flx-ext, forearm pron-sup, wrist flx-ext, and wrist rad-uln deviation. The exoskeleton joints are labeled 1–7 from proximal to distal in the order shown in Fig. 15.2. With seven joint rotations, there is one redundant degree of freedom.
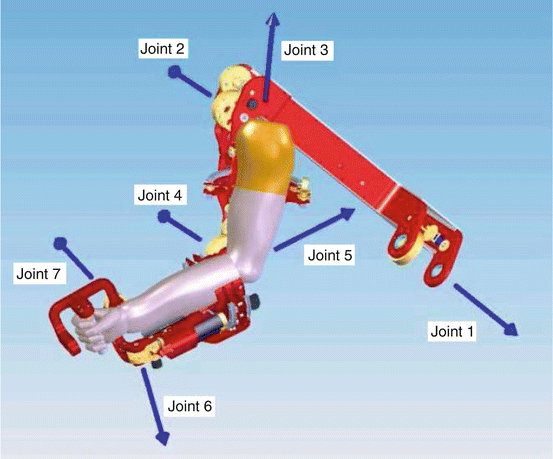
Fig. 15.2
Exoskeleton axes assignment relative to the human arm. Positive rotations about each joint produce the following motions: (1) combined flx/adb, (2) combined flx/add, (3) int rotation, (4) elbow flx, (5) forearm pron, (6) wrist ext, and (7) wrist rad dev
The fundamental principle in designing the exoskeleton joints is to align the rotational axis of the exoskeleton with the anatomical rotations axes. If more than one axis is at a particular anatomical joint (e.g. shoulder and wrist), the exoskeleton joints emulate the anatomical joint interaction at the center of the anatomical joint. Consistent with other work, the glenohumeral (G-H) joint is modeled as a spherical joint composed of three intersection axes [31]. The elbow is modeled by a single axis orthogonal to the third shoulder axis, with a joint stop to prevent hyperextension. Exoskeleton pron-sup takes place between the elbow and the wrist as it does. Finally, two intersecting orthogonal axes represent the wrist. The ranges of motion of the exoskeleton joints support 99 % of the ranges of motion required to perform daily activities [8].
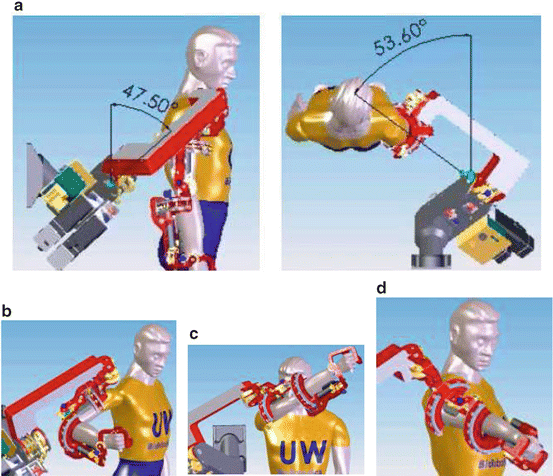
Fig. 15.3
Two singularities exist in the exoskeleton device, one when joints 1 and 3 align and the other when joints 3 and 5 align. (a) The orientation of joint 1 places the singularity at the shoulder in an anthropomorphically difficult place to reach. (b) Joints 1 and 3 align with simultaneous extension and abduction of the upper arm by 47. 5∘ and 53. 6 ∘. (c) Similarly, the same singularity can be reached through flexion and adduction by 132. 5∘ and 53. 6∘. (d) Alignment of joints 3 and 5 naturally occurs only in full elbow extension
Representing the ball and socket joint of the shoulder as three intersecting joins introduces of singularities that are not present in the human arm model. A significant consideration in the exoskeleton design is the placement of singularities [24]. The singularity is a device configuration in which a DOF is lost or compromised as a result of the alignment of two rotational axes. In the development of a three DOF spherical joint, the existence or nonexistence of singularities will depend entirely on the desired reachable workspace. Spherical workspace equal to or larger than a hemisphere will always contain singular positions. The challenge is to place the singularity in an unreachable, or near-unreachable location, such as the edge of the workspace. For the exoskeleton arm, singularities occur when joints 1 and 3 or joints 3 and 5 align. To minimize the frequency of this occurrence, the axis of joint 1 is positioned such that singularities with joint 3 take place only at locations that are anthropometrically hard to reach. For the placement shown in Fig. 15.3a, the singularity can be reached through simultaneous extension and abduction of the upper arm by 47. 5∘ and 53. 6∘, respectively (see Fig. 15.3b). Similarly, the same singularity can be reached through flexion and adduction by 132. 5∘ and 53. 6∘, respectively (see Fig. 15.3c). The singularity between joints 3 and 5 naturally occurs only in full elbow extension, i.e., on the edge of the forearm workspace (see Fig. 15.3d). With each of these singularity vectors at or near the edge of the human workspace, the middle and majority of the workspace is free of singularities [8, 9].
15.2.2.2 Representation of the Redundant Degree of Freedom
Given the position (x, y, z) and the orientation (ϕ x , ϕ y , and ϕ z ) of a target in a 3-dimensional (3D) workspace, the human arm has a redundant DOF which allows the elbow to move around an axis that goes through the center of the shoulder and the wrist joints. This redundant DOF provides the flexibility in human arm postures when completing the tasks defined in the 3D workspace. When applied to controlling the upper limb exoskeleton, a swivel angle is used to represent the redundant DOF. It specifies how much the elbow position pivots about the axis that goes through the center of shoulder and center of wrist, when the hand has a specific position and orientation.
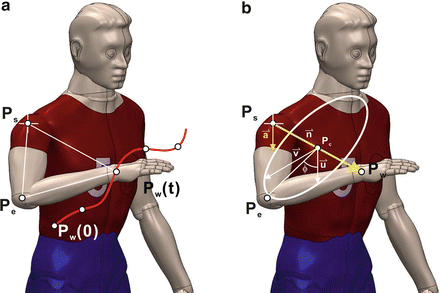
Fig. 15.4
(a) Given a fixed wrist position in a 3D workspace, the arm plane formed by the positions of the shoulder (P s ), the elbow (P e ) and the wrist (P w ) can move around an axis that connects the shoulder and the wrist due to the kinematic redundancy. (b) The redundant DOF can be represented by a swivel angle ϕ
As shown in Fig. 15.4, the arm plane is formed by the positions of the shoulder, the elbow and the wrist (denoted by P s , P e and P w , respectively). The direction of the axis that the arm plane pivots about (denoted by 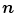 ) is defined as:
) is defined as:
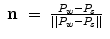
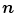 ) is defined as:
) is defined as: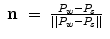
(15.1)
The plane orthogonal to 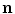 can be determined given the position of P e . P c is the intersection point of the orthogonal plane with the vector P w − P s .
can be determined given the position of P e . P c is the intersection point of the orthogonal plane with the vector P w − P s . 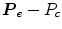 is the projection of the upper arm (
is the projection of the upper arm (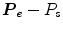 ) on the orthogonal plane.
) on the orthogonal plane. 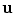 is the projection of a normalized reference vector
is the projection of a normalized reference vector 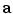 onto the orthogonal plane, which can be calculated as:
onto the orthogonal plane, which can be calculated as:
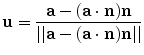
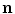 can be determined given the position of P e . P c is the intersection point of the orthogonal plane with the vector P w − P s .
can be determined given the position of P e . P c is the intersection point of the orthogonal plane with the vector P w − P s . 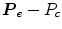 is the projection of the upper arm (
is the projection of the upper arm (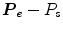 ) on the orthogonal plane.
) on the orthogonal plane. 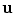 is the projection of a normalized reference vector
is the projection of a normalized reference vector 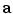 onto the orthogonal plane, which can be calculated as:
onto the orthogonal plane, which can be calculated as: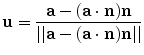
(15.2)
The swivel angle ϕ, represents the arm posture, can be defined by the angle between the vector 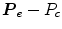 and
and 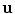 . The reference vector
. The reference vector 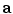 is suggested to be [0, 0, −1] T such that the swivel angle ϕ = 0∘ when the elbow is at its lowest possible point [32].
is suggested to be [0, 0, −1] T such that the swivel angle ϕ = 0∘ when the elbow is at its lowest possible point [32].
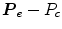 and
and 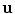 . The reference vector
. The reference vector 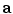 is suggested to be [0, 0, −1] T such that the swivel angle ϕ = 0∘ when the elbow is at its lowest possible point [32].
is suggested to be [0, 0, −1] T such that the swivel angle ϕ = 0∘ when the elbow is at its lowest possible point [32].Table 15.1
Denavit-Hartenberg (DH) Parameters for upper limb exoskeleton
Robot | i − 1 | i | α i | a i | d i | θ i |
|---|---|---|---|---|---|---|
Left arm | 0 | 1 | π∕2 | 0 | 0 | 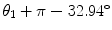 |
1 | 2 | π∕2 | 0 | 0 | 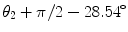 | |
2 | 3 | π∕2 | 0 | 0 | 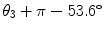 | |
3 | 4 | π∕2 | 0 | L 1 | θ 4 | |
4 | 5 | 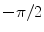 | 0 | 0 | 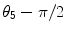 | |
5 | 6 | 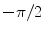 | 0 | L 2 | 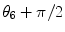 | |
6 | 7 | π∕2 | 0 | 0 | θ 7 +π | |
Right arm | 0 | 1 | π∕2 | 0 | 0 | θ 1 − 32. 94∘ |
1 | 2 | π∕2 | 0 | 0 | 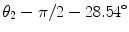 | |
2 | 3 | 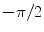 | 0 | 0 | 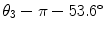 | |
3 | 4 | 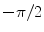 | 0 | − L 1 | θ 4 | |
4 | 5 | π∕2 | 0 | 0 | 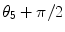 | |
5 | 6 | 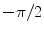 | 0 | − L 2 | 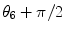 | |
6 | 7 | π∕2 | 0 | 0 | θ 7 +π |
15.2.2.3 The Forward and Inverse Kinematics of the Upper Limb Exoskeleton
This section derives the forward and inverse kinematics of the EXO-UL7 exoskeleton. Table 15.1 shows the Denavit-Hartenberg (DH) parameters of the upper limb exoskeleton, which are derived using the standard method (see [33]). The joint angle variables are θ i (i = 1, ⋯ , 7). L 1 and L 2 are the length of the upper and lower arms, respectively. The forward kinematics derives the transformation matrix7 0 T, which provides the position and the orientation of the wrist of the exoskeleton with respect to the base frame T base :
![$$\displaystyle\begin{array}{rcl} _{7}^{base}T& =& T_{\mathit{ base}} \cdot _{1}^{0}T \cdot _{ 2}^{1}T \cdot _{ 3}^{2}T \cdot _{ 4}^{3}T \cdot _{ 5}^{4}T \cdot _{ 6}^{5}T \cdot _{ 7}^{6}T \\ & =& \left [\begin{array}{*{10}c} r_{11} & r_{12} & r_{13} & P_{wx} \\ r_{21} & r_{22} & r_{23} & P_{wy} \\ r_{31} & r_{32} & r_{33} & P_{wz} \\ 0 & 0 & 0 & 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ3.gif)
![$$\displaystyle\begin{array}{rcl} _{7}^{base}T& =& T_{\mathit{ base}} \cdot _{1}^{0}T \cdot _{ 2}^{1}T \cdot _{ 3}^{2}T \cdot _{ 4}^{3}T \cdot _{ 5}^{4}T \cdot _{ 6}^{5}T \cdot _{ 7}^{6}T \\ & =& \left [\begin{array}{*{10}c} r_{11} & r_{12} & r_{13} & P_{wx} \\ r_{21} & r_{22} & r_{23} & P_{wy} \\ r_{31} & r_{32} & r_{33} & P_{wz} \\ 0 & 0 & 0 & 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ3.gif)
(15.3)
In order to move the singularity out of the range of the daily movements of the human arm, the bases of the two robotic arms of the upper limb exoskeleton are rotated according to Table 15.2.
Note that θ X , θ Y and θ Z represent the rotation about the X, Y and Z-axis, respectively. The transformation matrix for the base rotation is described in Eq. (15.4).
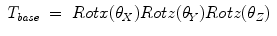
Table 15.2
Base rotation of the upper limb exoskeleton
θ X (∘) | θ Y (∘) | θ Z (∘) | |
|---|---|---|---|
Left arm | 132.5 | 45 | 90 |
Right arm | 132.5 | −45 | 90 |
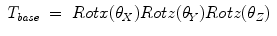
(15.4)
With the specification of the transformation matrix7 0 T, the inverse kinematics of the exoskeleton can be derived for the left and the right arm, respectively. The redundant DOF of the human arm can be constrained by specifying the elbow position (![$$P_{e} = [Pe_{x},Pe_{y},Pe_{z}]^{T}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_IEq24.gif) ).
).
![$$P_{e} = [Pe_{x},Pe_{y},Pe_{z}]^{T}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_IEq24.gif) ).
).Based on the shoulder position P s , elbow position P e , and wrist position P w , θ 4 can be derived as:
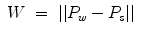
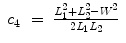
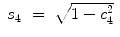
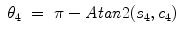
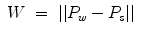
(15.5)
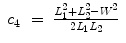
(15.6)
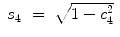
(15.7)
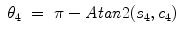
(15.8)
The transformation matrix4 3 T and its inverse 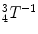 can be found based on θ 4.
can be found based on θ 4.
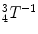 can be found based on θ 4.
can be found based on θ 4.The transformation matrix without the base rotation, denoted7 base T, can be found by:
![$$\displaystyle\begin{array}{rcl} _{7}^{0}T = T_{ 0}^{-1} \cdot _{ 7}^{\mathit{base}}T = \left [\begin{array}{*{10}c} r_{11}^{{\prime}}&r_{12}^{{\prime}}&r_{13}^{{\prime}}&_{7}^{0}P_{wx} \\ r_{21}^{{\prime}}&r_{22}^{{\prime}}&r_{23}^{{\prime}}&_{7}^{0}P_{wy} \\ r_{31}^{{\prime}}&r_{32}^{{\prime}}&r_{33}^{{\prime}}&_{7}^{0}P_{wz} \\ 0 & 0 & 0 & 1 \end{array} \right ]& &{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ9.gif)
![$$\displaystyle\begin{array}{rcl} _{7}^{0}T = T_{ 0}^{-1} \cdot _{ 7}^{\mathit{base}}T = \left [\begin{array}{*{10}c} r_{11}^{{\prime}}&r_{12}^{{\prime}}&r_{13}^{{\prime}}&_{7}^{0}P_{wx} \\ r_{21}^{{\prime}}&r_{22}^{{\prime}}&r_{23}^{{\prime}}&_{7}^{0}P_{wy} \\ r_{31}^{{\prime}}&r_{32}^{{\prime}}&r_{33}^{{\prime}}&_{7}^{0}P_{wz} \\ 0 & 0 & 0 & 1 \end{array} \right ]& &{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ9.gif)
(15.9)
Thus, the wrist position with respect to the rotated base is 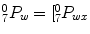 ,
, 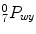 ,
, ![$$_{7}^{0}P_{wz}]^{T}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_IEq28.gif) .
.
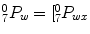 ,
, 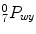 ,
, ![$$_{7}^{0}P_{wz}]^{T}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_IEq28.gif) .
.Similarly, the elbow position with respect to the rotated base, denoted by 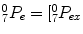 ,
, 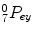 ,
, ![$$_{7}^{0}P_{ez}]^{T}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_IEq31.gif) , is:
, is:
![$$\displaystyle\begin{array}{rcl} \left [\begin{array}{*{10}c} _{7}^{0}P_{ex} \\ _{7}^{0}P_{ey} \\ _{7}^{0}P_{ez} \\ 1 \end{array} \right ]& =& T_{0}^{-1} \cdot \left [\begin{array}{*{10}c} _{7}^{base}P_{ex} \\ _{7}^{base}P_{ey} \\ _{7}^{base}P_{ez} \\ 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ10.gif)
Note that 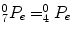 and
and
![$$\begin{array}{rcl} {}_{4}^{0}T& = & {}_{ 1}^{0}T \cdot _{ 2}^{1}T \cdot {}_{ 3}^{2}T \cdot {}_{4}^{3}T = \left[\begin{array}{cccc} & & & {}_{4}^{0}P_{ex} \\ & {}_{4}^{0}R& & {}_{4}^{0}P_{ey} \\ & & & {}_{4}^{0}P_{ez} \\ 0& 0 &0& 1 \end{array} \right] = \left[\begin{array}{cccc} & & & L_{1}c_{1}s_{2} \\ & {}_{4}^{0}R& & L_{1}c_{2} \\ & & & L_{1}s_{1}s_{2} \\ 0& 0 &0& 1 \end{array} \right]\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ11.gif)
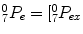 ,
, 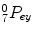 ,
, ![$$_{7}^{0}P_{ez}]^{T}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_IEq31.gif) , is:
, is:![$$\displaystyle\begin{array}{rcl} \left [\begin{array}{*{10}c} _{7}^{0}P_{ex} \\ _{7}^{0}P_{ey} \\ _{7}^{0}P_{ez} \\ 1 \end{array} \right ]& =& T_{0}^{-1} \cdot \left [\begin{array}{*{10}c} _{7}^{base}P_{ex} \\ _{7}^{base}P_{ey} \\ _{7}^{base}P_{ez} \\ 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ10.gif)
(15.10)
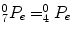 and
and![$$\begin{array}{rcl} {}_{4}^{0}T& = & {}_{ 1}^{0}T \cdot _{ 2}^{1}T \cdot {}_{ 3}^{2}T \cdot {}_{4}^{3}T = \left[\begin{array}{cccc} & & & {}_{4}^{0}P_{ex} \\ & {}_{4}^{0}R& & {}_{4}^{0}P_{ey} \\ & & & {}_{4}^{0}P_{ez} \\ 0& 0 &0& 1 \end{array} \right] = \left[\begin{array}{cccc} & & & L_{1}c_{1}s_{2} \\ & {}_{4}^{0}R& & L_{1}c_{2} \\ & & & L_{1}s_{1}s_{2} \\ 0& 0 &0& 1 \end{array} \right]\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ11.gif)
(15.11)
For the both arms,
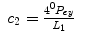
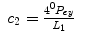
(15.12)
For the left arm,
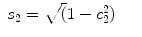
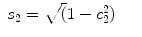
(15.13)
For the right arm,
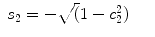
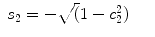
(15.14)
Thus, θ 2 can be resolved as:
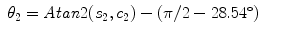
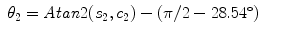
(15.15)
To resolve θ 1, for the both arms,
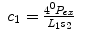
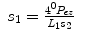
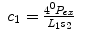
(15.16)
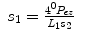
(15.17)
Thus, for the left arm,
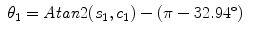
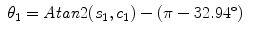
(15.18)
For the right arm,
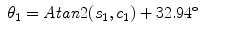
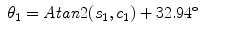
(15.19)
The transformation matrices1 0 T and2 1 T and their inverses1 0 T −1 and2 1 T −1 can be found accordingly.
Thus, the wrist position with respect to Frame 2, denoted 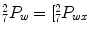 ,
, 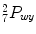 ,
, ![$$_{7}^{2}P_{wz}]^{T}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_IEq35.gif) , can be found:
, can be found:
![$$\begin{array}{rcl} {}_{7}^{2}T& =& {}_{ 2}^{1}T^{-1} \cdot {}_{ 1}^{0}T^{-1} \cdot {}_{ 7}^{0}T = \left[\begin{array}{cccc} & & & {}_{7}^{2}P_{wx} \\ & {}_{7}^{2}R& & {}_{7}^{2}P_{wy} \\ & & & {}_{7}^{2}P_{wz} \\ 0& 0 &0& 1 \end{array} \right]\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ20.gif)
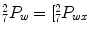 ,
, 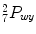 ,
, ![$$_{7}^{2}P_{wz}]^{T}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_IEq35.gif) , can be found:
, can be found:![$$\begin{array}{rcl} {}_{7}^{2}T& =& {}_{ 2}^{1}T^{-1} \cdot {}_{ 1}^{0}T^{-1} \cdot {}_{ 7}^{0}T = \left[\begin{array}{cccc} & & & {}_{7}^{2}P_{wx} \\ & {}_{7}^{2}R& & {}_{7}^{2}P_{wy} \\ & & & {}_{7}^{2}P_{wz} \\ 0& 0 &0& 1 \end{array} \right]\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ20.gif)
(15.20)
For the left arm,
![$$\displaystyle\begin{array}{rcl} _{7}^{2}P_{ w} = \left [\begin{array}{*{10}c} -L_{2}c_{3}s_{4} \\ -L_{1} - L_{2}c_{4} \\ -L_{2}s_{3}s_{4}\\ \end{array} \right ]& &{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ21.gif)
![$$\displaystyle\begin{array}{rcl} _{7}^{2}P_{ w} = \left [\begin{array}{*{10}c} -L_{2}c_{3}s_{4} \\ -L_{1} - L_{2}c_{4} \\ -L_{2}s_{3}s_{4}\\ \end{array} \right ]& &{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ21.gif)
(15.21)
For the right arm,
![$$\displaystyle\begin{array}{rcl} _{7}^{2}P_{ w} = \left [\begin{array}{*{10}c} -L_{2}c_{3}s_{4} \\ -L_{1} - L_{2}c_{4} \\ L_{2}s_{3}s_{4}\\ \end{array} \right ]& &{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ22.gif)
![$$\displaystyle\begin{array}{rcl} _{7}^{2}P_{ w} = \left [\begin{array}{*{10}c} -L_{2}c_{3}s_{4} \\ -L_{1} - L_{2}c_{4} \\ L_{2}s_{3}s_{4}\\ \end{array} \right ]& &{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ22.gif)
(15.22)
To resolve θ 3, for the both arms,
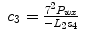
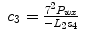
(15.23)
For the left arm,
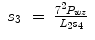
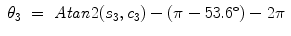
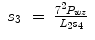
(15.24)
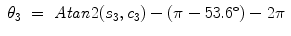
(15.25)
For the right arm,
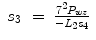
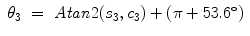
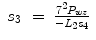
(15.26)
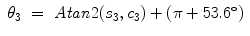
(15.27)
The transformation matrix3 2 T and its inverse3 2 T −1 can be found accordingly.
θ 5, θ 6 and θ 7 can be derived from the transformation matrices from Frame 4 to Frame 77 4 T.
![$$\displaystyle\begin{array}{rcl} _{7}^{4}T& =& _{ 4}^{3}T^{-1} \cdot _{ 3}^{2}T^{-1} \cdot _{ 2}^{1}T^{-1} \cdot _{ 1}^{0}T^{-1} \cdot _{ 7}^{0}T = \left [\begin{array}{*{10}c} _{7}^{4}r_{11} & _{7}^{4}r_{12} & _{7}^{4}r_{13} & _{7}^{4}P_{wx} \\ _{7}^{4}r_{21} & _{7}^{4}r_{22} & _{7}^{4}r_{23} & _{7}^{4}P_{wy} \\ _{7}^{4}r_{31} & _{7}^{4}r_{32} & _{7}^{4}r_{33} & _{7}^{4}P_{wz} \\ 0 & 0 & 0 & 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ28.gif)
![$$\displaystyle\begin{array}{rcl} _{7}^{4}T& =& _{ 4}^{3}T^{-1} \cdot _{ 3}^{2}T^{-1} \cdot _{ 2}^{1}T^{-1} \cdot _{ 1}^{0}T^{-1} \cdot _{ 7}^{0}T = \left [\begin{array}{*{10}c} _{7}^{4}r_{11} & _{7}^{4}r_{12} & _{7}^{4}r_{13} & _{7}^{4}P_{wx} \\ _{7}^{4}r_{21} & _{7}^{4}r_{22} & _{7}^{4}r_{23} & _{7}^{4}P_{wy} \\ _{7}^{4}r_{31} & _{7}^{4}r_{32} & _{7}^{4}r_{33} & _{7}^{4}P_{wz} \\ 0 & 0 & 0 & 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ28.gif)
(15.28)
For the left arm,
![$$\displaystyle\begin{array}{rcl} _{7}^{4}T& =& _{ 4}^{3}T^{-1} \cdot _{ 3}^{2}T^{-1} \cdot _{ 2}^{1}T^{-1} \cdot _{ 1}^{0}T^{-1} \cdot _{ 7}^{0}T \\ & =& \left [\begin{array}{*{10}c} c_{5}c_{6}c_{7} - s_{5}s_{7} & -c_{7}s_{5} - c_{5}c_{6}s_{7} & c_{5}s_{6} & 0 \\ -c_{7}s_{6} & s_{6}s_{7} & c_{6} & L_{2} \\ -c_{5}s_{7} - c_{6}c_{7}s_{5} & c_{5}c_{7} - c_{6}s_{5}s_{7} & -s_{5}s_{6} & 0 \\ 0 & 0 & 0 & 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ29.gif)
![$$\displaystyle\begin{array}{rcl} _{7}^{4}T& =& _{ 4}^{3}T^{-1} \cdot _{ 3}^{2}T^{-1} \cdot _{ 2}^{1}T^{-1} \cdot _{ 1}^{0}T^{-1} \cdot _{ 7}^{0}T \\ & =& \left [\begin{array}{*{10}c} c_{5}c_{6}c_{7} - s_{5}s_{7} & -c_{7}s_{5} - c_{5}c_{6}s_{7} & c_{5}s_{6} & 0 \\ -c_{7}s_{6} & s_{6}s_{7} & c_{6} & L_{2} \\ -c_{5}s_{7} - c_{6}c_{7}s_{5} & c_{5}c_{7} - c_{6}s_{5}s_{7} & -s_{5}s_{6} & 0 \\ 0 & 0 & 0 & 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ29.gif)
(15.29)
For the right arm,
![$$\displaystyle\begin{array}{rcl} _{7}^{4}T& =& _{ 4}^{3}T^{-1} \cdot _{ 3}^{2}T^{-1} \cdot _{ 2}^{1}T^{-1} \cdot _{ 1}^{0}T^{-1} \cdot _{ 7}^{0}T \\ & =& \left [\begin{array}{*{10}c} c_{5}c_{6}c_{7} - s_{5}s_{7} & -c_{7}s_{5} - c_{5}c_{6}s_{7} & c_{5}s_{6} & 0 \\ c_{7}s_{6} & -s_{6}s_{7} & -c_{6} & L_{2} \\ c_{5}s_{7} + c_{6}c_{7}s_{5} & c_{5}c_{7} - c_{6}s_{5}s_{7} & s_{5}s_{6} & 0 \\ 0 & 0 & 0 & 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ30.gif)
![$$\displaystyle\begin{array}{rcl} _{7}^{4}T& =& _{ 4}^{3}T^{-1} \cdot _{ 3}^{2}T^{-1} \cdot _{ 2}^{1}T^{-1} \cdot _{ 1}^{0}T^{-1} \cdot _{ 7}^{0}T \\ & =& \left [\begin{array}{*{10}c} c_{5}c_{6}c_{7} - s_{5}s_{7} & -c_{7}s_{5} - c_{5}c_{6}s_{7} & c_{5}s_{6} & 0 \\ c_{7}s_{6} & -s_{6}s_{7} & -c_{6} & L_{2} \\ c_{5}s_{7} + c_{6}c_{7}s_{5} & c_{5}c_{7} - c_{6}s_{5}s_{7} & s_{5}s_{6} & 0 \\ 0 & 0 & 0 & 1 \end{array} \right ]{}\end{array}$$](/wp-content/uploads/2016/11/A324794_1_En_15_Chapter_Equ30.gif)
(15.30)
Thus, for the left arm,
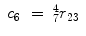
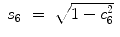
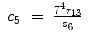
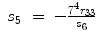
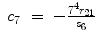
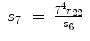
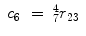
(15.31)
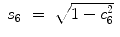
(15.32)
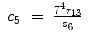
(15.33)
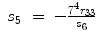
(15.34)
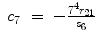
(15.35)
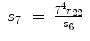
(15.36)
For the right arm,
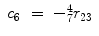
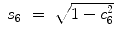
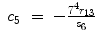
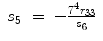
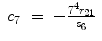
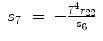
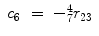
(15.37)
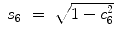
(15.38)
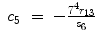
(15.39)
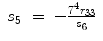
(15.40)
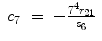
(15.41)
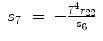
(15.42)