(1)
Department of Neurology, Wake Forest University School of Medicine, Winston-Salem, NC, USA
Abstract
This chapter provides an introduction to the steps involved in creating dependable systems. This starts with a description of functional hazard assessment (FHA). The steps involved in preliminary system safety assessment (PSSA) and system safety assessment (SSA) are reviewed. The chapter introduces fault tree analysis (FTA) and failure modes and effects analysis (FMEA) as important tools in the safety assessment process. This chapter also introduces the basics of probability theory which can guide quantitative assessment. The concepts behind common cause analysis are introduced. To make the book self-contained, more detailed mathematical concepts are presented in the appendices which can be skipped by less mathematically inclined readers.
Keywords
Preliminary system safety assessment (PSSA)System safety assessment (SSA)Functional hazard assessmentFault tree analysis (FTA)Failure modes and effects analysis (FMEA)Common cause analysis (CCA)Common mode analysis (CMA)Zonal safety analysis (ZSA)Particular risks analysis (PRA)Bayesian statisticsIV MethylprednisoloneBoolean algebraReliability block diagramIntroduction
Chapter 1 described the properties of dependable systems. This chapter introduces systematic methods used in the design and development of dependable systems. Industries such as nuclear, aviation, railways, and their regulatory agencies have over the years developed standards, analytical techniques for safety assessment with interdisciplinary applications which will be introduced in this chapter. These are the methods which are used in system design when a new product or service is conceived.
This chapter borrows heavily from the aerospace industry which has amongst the most rigorous standards. An important guiding document for safety in development of new aircraft is ARP 4761 [1]. The methods employed are qualitative, quantitative, or both. These include functional hazard assessment (FHA), failure modes and effects analysis (FMEA), fault tree analysis (FTA), dependence diagrams (DD), Markov analysis (MA), and common cause analysis (CCA) (which is composed of zonal safety analysis (ZSA), particular risks analysis (PRA), and common mode analysis (CMA)).
The development process is iterative in nature with system safety being an inherent part of the process. The process begins with concept design and derives an initial set of safety requirements for it. During design development, changes are made to it and the modified design must be reassessed to meet safety objectives. This may create new design requirements. These in turn necessitate further design changes. The safety assessment process ends with verification that the design meets safety requirements and regulatory standards [1]. The safety assessment process begins with FHA, preliminary system safety assessment (PSSA), and system safety assessment (SSA). These techniques are applied iteratively. Once FHA is performed, PSSA is performed to evaluate the proposed design or system architecture. The SSA is performed to evaluate whether the final design meets requirements.
The subject matter in this chapter can be initially challenging. The reader is encouraged to skim the contents at first glance and proceed to subsequent chapters which elaborate on the concepts described here in a medical framework and return frequently to reinforce concepts.
Functional Hazard Assessment
FHA is performed at the beginning of system development. Its main objective is to “identify and classify failure conditions associated with the system by their severity” [1]. The identification of these failure conditions is vital to establish the safety objectives. This is usually performed at two levels, for the example of the aircraft industry—at the completed aircraft level and at the individual system level [1].
The aircraft level FHA identifies failure conditions of the aircraft. The system level FHA is an iterative qualitative assessment which identifies the effects of single and combined system failures on aircraft function. The results of the aircraft and system level FHA are the starting point for the generation of safety requirements. Based on this data, fault trees, FMEA can be performed for the identified failure conditions which are studied later.
ARP 4761 provides guidelines on how an FHA should be conducted. Since this is an iterative process, it is performed in broad categories with increasing resolution as the analysis proceeds to finer and finer subsystems. A recommended manner to accomplish this is to list all the performance requirements based on design characteristics. Once the high-level requirements have been identified, the failure conditions associated with them are identified. This is then used to generate lower level requirements. This process is then applied iteratively till the design is complete. An illustrative example for aircraft is as shown below:
Aircraft function | Failure condition |
|---|---|
1. To control aircraft trajectory | Loss of aircraft control |
Loss of pitch control (partial control loss) | |
Runaway of one control surface |
These failure conditions are further broken down in a systematic manner through FHA performed at the system level. FHA therefore is a top-down process; it proceeds from the broad to more specific functions and their failures. The following steps are involved [1]:
Determine and Characterize Inputs at Product Level or System Level
For an aircraft this involves specification of top level functions such as passenger load, thrust, lift, customer requirements, etc. For an automobile, this involves description of the type of vehicle (sedan, minivan, etc.), performance requirements such as horsepower, torque, braking, steering; control systems, transmission, safety systems. For individual systems such as braking, system level approach involves looking at subsystems such as hydraulics, interface with electronic control systems such as antilock braking system (ABS), power brakes, and so on.
FHA Process
Once the inputs (as above) have been identified, the following steps are then applied.
Identify all the functions with the level under study [1]. These include functions provided by the system and all the other systems interlinked to the system under study.
Identify and describe failure conditions associated with these functions, considering single and multiple failures under different conditions [1]. Examples include “loss of hydraulics” under “normal weather” or “ice/snow storm” conditions.
Determine the effects of the failure conditions.
Classify failure condition effects. This is shown in Chap. 1, Table 1.1. Common classification systems in use across several domains (aviation, railway) are catastrophic (e.g., loss of engines), severe, major, hazardous, minor, and no safety effect (e.g., loss of in-flight entertainment system). Based on failure condition classification, allowable probability limits of occurrence and required developmental assurance levels (DAL) are assigned as described in Chap. 1.
Assignment of requirements to the failure conditions at the next lower level of analysis. Why is this failure catastrophic or why is it only minor? Identify supporting materials for failure condition effect classification. This can be from simulations, prior experience with similar aircraft, etc.
Identify methods used to verify compliance with failure condition requirements.
A careful examination of the above method shows that a good FHA is a collaborative, multidisciplinary effort requiring great domain knowledge and insight requiring great qualitative effort. The FHA leads to the PSSA.
FHA in Neurological Diagnosis and Treatment
FHA is a very useful method for analyzing and mitigating morbidity from medical illness, especially neurological illness. In cases where the underlying disease is not directly treatable, FHA is a systematic method for identifying the morbidity from the untreatable illness. The underlying disease causes loss of normal function or permits gain of abnormal function both of which cause significant distress to the patient. Examples of loss of function include weakness, poor balance, difficulty swallowing, and difficulty speaking, etc. Examples of gain of function include severe pain from neuropathy, painful myositis, etc. The failure classification helps quantify the clinical significance of the change in function. Painful neuropathy, through distressing and leading to a poor quality of life would not be expected to shorten life expectancy or cause significant problems with mobility. Therefore this can be classified as minor. Difficulty swallowing on the other hand can lead to progressive weight loss and aspiration which can be fatal. Therefore this failure condition can be classified as major or catastrophic. This helps direct resources and plan treatment costs appropriately. The following case examples are illustrative.
Case Example 1
J.C.C. is a 75-year-old avid saxophone player. He noticed insidious onset of loss of dexterity in his left hand while playing the saxophone for the last several months. He denied any abnormal posturing or pain in the left upper extremity while playing the saxophone. He reported that he was unable to seamlessly move between octaves and was unable to initiate fine movements with his fingers for precise playing of certain rhythms. He denied any pain, numbness, or weakness in the left upper extremity. He had not noticed any loss of dexterity with less challenging tasks such as manipulating a fork and knife while eating. He denied any symptoms in his right upper extremity.
He reported sleep problems with a tendency to sleep walk and sustained a fracture in his right little finger approximately a year ago while possibly acting out his dreams during sleep. He denied any significant changes in smell. He denied any falls. He also denied any visual hallucinations or memory loss. He had noticed some twitching, which may actually resemble a tremor in the left upper extremity, but this was very infrequent. He denied any memory problems or cognitive difficulties and remained actively involved in the stock market with surprisingly good returns. However he reported severe depression for the last several years.
On examination, mental status and cranial nerve examination were normal save decreased blink rate and facial expression. He had significant diffuse bradykinesia. He had normal 5/5 strength in his bilateral upper extremities without evidence of fasciculations or atrophy. He also had reduced ability to tap his fingers on the left side when compared to the right. Examination of motor tone revealed left upper extremity cogwheel rigidity, exacerbated by exercising his right upper extremity. He had normal tone in the right upper and bilateral lower extremities. Gait examination revealed a festinant gait without retropulsion. There was no evidence of apraxia. Based on this history, physical examination, a diagnosis of Parkinson’s disease was made. FHA of J.C.C. reveals the following:
Normal function | Failure condition |
|---|---|
1. Fine motor control of fingers of left hand | 1. Partial loss of fine motor function of left hand |
2. Speed and rhythm of movement | 2. Partial slowing of movement in all limbs |
3. Normal mood and cheer | 3. Severely depressed mood and cheer |
4. Normal sleep | 4. REM behavior disorder |
The FHA can guide therapy. In J.C.C.’s case, treatment of depression with citalopram and REM behavior disorder with clonazepam had the greatest impact on his life. He did not tolerate levodopa well and had a modest response to pramipexole which enabled him to continue his hobby for several more years.
Case Example 2
S.C. is a 61 y/o male who developed bilateral shoulder pain, soreness 5–6 weeks ago. Subsequently he developed shortness of breath, especially when lying down. Symptoms are worst during the night when he wakes severely dyspneic after 3–4 h of sleep. Most routine activities during the day are well tolerated; however he would get severely short of breath with minor exertion. He denied any changes in his vision, any difficulty chewing or swallowing. He also denied any weakness elsewhere or any changes in sensation or bladder function. He denied any antecedent vaccinations, flu-like illnesses or tick bites. He was evaluated by his pulmonologist who noticed high diaphragms on a chest X-ray that was performed as part of routine evaluation. On examination, he had normal mental status, cranial nerves, extremity strength, sensation, and mildly brisk symmetric reflexes with downgoing toes. He was severely orthopneic with paradoxical movements of the diaphragm and observed to need accessory muscles of respiration like the sternocleidomastoid. NCS/EMG showed normal nerve conduction studies and fibrillations and positive sharp waves in the diaphragm with a complete absence of any recruitable motor units. Based on his clinical, radiographic, and EMG findings he was diagnosed with bilateral diaphragmatic palsy, likely as a consequence of idiopathic brachial neuritis (Parsonage Turner syndrome) because of prodromal shoulder pain. MRI Cervical Spine, spinal fluid studies were normal and an empirical trial of intravenous immunoglobulin (IVIG) and prednisone did not yield any benefit. CT Chest and neck excluded any mass lesions infiltrating the phrenic nerves. FHA helped mitigate his diaphragmatic failure condition.
Normal function | Failure condition |
|---|---|
1. Ventilatory function during daytime | 1. Partial loss of ventilatory function during daytime (especially exertion) |
2. Ventilatory function during nighttime | 2. Severe loss of ventilatory function at night time |
Based on the results of overnight pulse oximetry, he was started on night time BiPAP with adequate restoration of quality of life. Further pharmacotherapy with repeat IVIG, prolonged steroid therapy or other immunosuppression was not performed.
Case Example 3
D.B.S. is a 60 y/o male presenting with numbness, tingling, and painful paresthesias involving his toes for the last several months. Symptoms started in the right lower extremity, experienced most towards the great toe followed by involvement of the left lower extremity 6 months later. Symptoms are worse when wearing tight shoes, standing and walking for prolonged periods. Feet would feel hot or experience a pressure like discomfort. He denied any urinary, bowel disturbances. He also denied dry eyes and dry mouth. He experienced back trauma in the 1990s which was monitored nonoperatively. Symptoms are not experienced at rest, especially at night. He felt mild involvement of the hands at the time of his appointment. He denied any neck pain. He had an extensive evaluation through his primary care physician which excluded diabetes mellitus and vitamin deficiency. Physical examination revealed normal strength and reflexes down to the ankles. Sensory examination revealed normal joint position sense, mild loss of distal pinprick sensation involving the feet. A nerve conduction study revealed mild demyelinating features suggestive of distal acquired demyelinating symmetrical (DADS) variant of chronic inflammatory demyelinating polyneuropathy (CIDP). Blood work revealed a faint IgM Lambda spike. Follow-up testing revealed very high titers of anti-myelin-associated glycoprotein (anti-MAG) antibodies which frequently causes such a presentation. Therapeutic approaches to the anti-MAG syndrome are very challenging ranging from IVIG, plasmapheresis, steroids, and rituximab [2]. FHA yields the following:
Normal function | Failure condition |
|---|---|
1. Normal perception in feet | 1. Partial loss of normal sensation in the feet1.1 Partial loss of skin sensation in the feet |
2. Absence of abnormal sensation like tingling, pain involving feet | 2. Moderate pain and tingling involving feet |
3. Normal serum protein profile in blood | 3. Abnormal IgM Lambda spike on serum immunofixation |
Since the therapeutic choices are so varied and so expensive, FHA is very useful in guiding therapy.
Given the mild failure conditions observed on FHA, immunotherapy for CIDP was deferred. The patient experienced very little clinical progression despite abnormal test results over 2 years. At the end of 2 years he was placed on Gabapentin 300 mg once to twice daily for symptomatic relief of moderate pain and tingling involving the feet.
Preliminary System Safety Assessment
PSSA is a systematic examination of the proposed system architecture to examine how failures can lead to the functional hazards identified by the FHA and how safety requirements can be met [1]. The PSSA addresses each failure condition identified by the FHA in qualitative or quantitative terms [1]. It involves the use of tools such as FTA, DD, and MA to identify possible faults. The use of these is discussed later. The identification of hardware and software faults and their possible contributions to various failure conditions identified in the FHA provides the data for deriving the appropriate DAL for individual systems. The process is iterative being performed at the aircraft level (for the case of airplanes) followed by individual system levels. The process involves the following steps [1, 3]:
Inputs to PSSA
Aircraft level FHA, System level FHA.
PSSA Process
The PSSA is a top-down process which determines how system failures can lead to the functional impairments or failures identified by the FHA. The following steps are involved in performing a PSSA for the example of aircraft [1]:
1.
Identify and list aircraft and system level safety level requirements:
This is derived from the FHA and preliminary CCA (common cause analysis, discussed in detail below in Section “Common Cause Analysis (CMA, ZSA, and PRA)”) processes which create the initial safety requirements for the systems. This information is combined with the knowledge of system architecture and performance features. The inputs to this step therefore include the failure conditions from FHA and CCA, system architecture description, description of system equipment, system interfaces with other systems and preliminary CCA (described in Section “Common Cause Analysis (CMA, ZSA, and PRA)”) [1].
2.
Determine if the design can be expected to meet identified safety requirements and objectives
In this step, each identified severe-major/hazardous and catastrophic failure condition is evaluated in detail. Each of these is analyzed using FTA (discussed in detail below in Section “Fault Tree Analysis”) or a similar method to show how item failures either singly or in combination lead to system or at a higher level aircraft failure. This analysis is both qualitative and quantitative. This step demonstrates that all the qualitative and quantitative objectives associated with the failure conditions can be met by the design under consideration. Maintenance intervals for discovery of hidden (latent) failures are also identified in this step. Based on the component systems and their failure consequences identified in the fault trees, the corresponding development assurance level and budgets are developed. All requirements for independence of systems made in the FTA are verified in this step. This step is frequently performed at an early stage in the design, therefore the inputs are based on preliminary domain knowledge, experience with similar designs and judgment available at the time [1].
3.
Derive safety requirements for the design of lower level systems
The safety requirements identified at the system level by the preceding steps are then allocated to the items or components making up a system. This involves both hardware and software and is both qualitative and quantitative. It also involves specifications for installation of systems and subsystems (aspects such as segregation, separation of systems, protection from mechanical damage, etc.). Safety allocations include DAL for hardware and software, maintenance intervals and associated “Not to Exceed” times [1].
The PSSA process should be well-documented since this step is frequently revisited during the development process and the reasons for specific design architectures may need to be understood from different perspectives and requirements at different stages of the project.
Fault Tree Analysis
FTA is very powerful, graphical deductive reasoning tool which can identify undesired failure and help the investigator identify their root causes. The technique was developed extensively by the nuclear and aerospace industries and can be viewed as a systematic method for acquiring information about a system. References [4] and [5] provide a wealth of information about this technique. An introduction to the basic theory of fault trees, including some of the rules of probability theory, Boolean algebra is presented here to introduce the reader to this technique. Medical examples will be presented in Chap. 3.
There are two major methods for performing analysis—inductive and deductive analysis. Inductive analysis involves reasoning from individual cases to a general conclusion [4]. In this method, a particular fault is considered and we attempt to ascertain the effect of that fault or condition on system operation. Examples of this include a fuel pump malfunction and its effects on power output of an engine. Or the effect of failure of an organ and its effect on body function such as renal failure and its consequences on urine output. FMEA, failure modes effects and criticality analysis (FMECA) are some commonly used inductive methods which will be discussed further.
Deductive reasoning method constitutes reasoning from the general to the specific. In this method, we observe that the system has failed in a particular way and we attempt to determine what components failed and in what manner that led to system failure. This is also called “Sherlock Holmesian” thought since the legendary detective had to start with a crime and based on the clues and evidence available reconstruct the events that led to the crime [4]. This mode of analysis is well suited for the investigation of accidents and similar untoward events. FTA is an example of deductive reasoning. Therefore, it lends itself well to medical diagnosis. Inductive reasoning helps tell the investigator what system states can occur, deductive reasoning tells how a particular system state, especially a failure state can occur [4].
A fault tree is a graphical analytic technique composed of the various parallel and sequential combinations of events that will result in the undesired event of system failure. The method is both qualitative and quantitative. The undesired event is called the “top event” of a fault tree. Constructing a fault tree requires deep knowledge and insight into the event being investigated since the investigator develops the tree based on knowledge of systems and their connections. The faults can be component hardware failures, software failures, or human failures. The tree itself represents the logical interrelationships between basic events which can cause the top event of system failure. It is not an exhaustive enumeration of possibilities, but an exploration of the more likely events which can cause the top event.
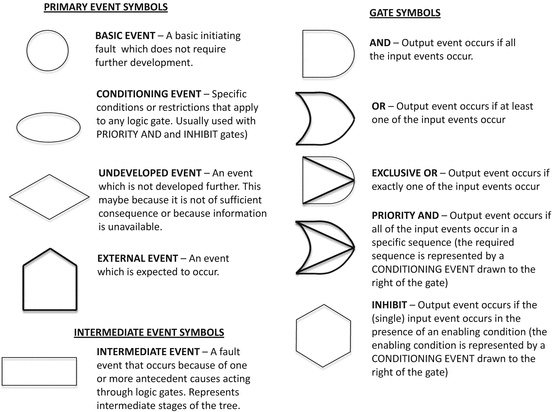
The building blocks of a fault tree are primary events, intermediate events, and top events. The building blocks are described here, the symbols are shown in Fig. 2.1. The list is not exhaustive, only the most commonly used events and logic gates are discussed here.
The Primary Events
The primary events of a fault tree are those events which are not further developed. These include the following [4]:
1.
Basic event: This is a basic initiating fault which does not require further development. Examples include fuel valve blocked, microprocessor failure, etc. for top events of engine failure or computer failure. It is represented by a circle.
(a)
Medical example: Subtherapeutic INR (basic event) led to thrombus which led to stroke.
2.
Conditioning event: Specific conditions or restrictions that apply to the logic gates. It is represented by an oval. Used with “Priority AND” and “INHIBIT” gates.
3.
Undeveloped events: An event which is not developed further, either because developing it further is not relevant for the problem being analyzed or because more information is not available. It is represented by a diamond.
(a)
Medical example: A finding uncovered but not relevant to current analysis. Osteoporosis on Chest CT done for lung cancer. Therefore not explored further.
4.
External event: is an event which is normally expected to occur. For aviation example this includes events such as “icing.” These events are not in themselves faults, these events can occur normally. It is represented by the house symbol.
Note that basic events are supposed to be independent in many system safety assumptions which may not be true in the real world.
Intermediate Event Symbols
Intermediate event: a fault event that happens because of one or more primary events acting through logic gates. It is represented by the rectangle symbol.
(a)
Medical example: Intermediate event: Blood loss (basic event) led to hypotension (Intermediate event) which led to shock liver.
Logic Gates Used in Fault Trees
1.
Boolean “OR” gate: Output occurs if at least one of the input events occurs.
(a)
Medical example: Spinal cord disease OR muscle disease led to weakness.
2.
Boolean “AND” gate: For this gate, the output occurs if all the inputs are true. The output event occurs if and only if all the input events occur.
(a)
Medical example: Right ureter blockage AND left ureter blockage led to kidney failure.
3.
The Inhibit gate: represented by a hexagon is a special case of the AND gate. The output can be caused by a single input, but a qualifying condition must be present for the output to happen. The conditional input discussed under primary events is the qualifying condition that must be present for the output to happen. Examples include input chemical reagents (input) going to completion (output) in the presence of a catalyst [4].
(a)
Medical example of Inhibit gate: (a) Diaphragm weakness from myasthenia gravis in the presence of moderate COPD led to ventilatory failure. Either could not do it alone for a patient with moderate myasthenia gravis and COPD. (b) Stable Congestive Heart Failure (CHF) patient developed hypokalemia (conditioning event) which led to ventricular arrhythmia.
Less frequently used logic gates are the Exclusive OR and Priority AND gates. In an Exclusive OR gate, the output occurs only if one of the inputs occur. When more than one of the inputs happens, the output is zero.
Fault Tree Component Fault Categories
In FTA, faults are classified into three categories—primary, secondary, and command. A primary fault occurs in an environment for which the component is designed. For example, a concrete beam in a building failing under the weight of a load which is less than what the beam is designed for. A secondary failure is a component or system failure in an environment which it is not designed for [4]. For the example above, this involves the beam failing under a weight more than what it was designed for [4]. A command failure is the proper operation of a component at the wrong time or place.
Failure effects, failure modes, and failure mechanisms are important concepts in analyzing the relationships between events. Consider Fig. 2.2 which shows a simple circuit controlling operation of a lamp based on an illustrative example in [4].
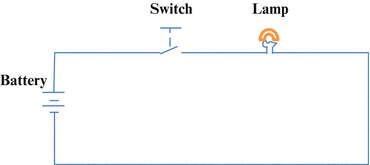

Fig. 2.2
Simple system to illustrate failure effects, modes, and mechanisms. The battery provides the energy for operation of a lamp controlled through a switch
Failure effects understands failures based on their importance—what are the consequences or effects of failure on the system [4]. Failure modes helps describe the specific manner in which failure occurs. Failure mechanisms helps identify the cause(s) of the failure modes [4]. For the example of Fig. 2.2, this is shown in Table 2.1. For example, the failure effect of low voltage from battery can occur due to the failure mode of leakage of electrolyte from battery. Defects in casing of the battery or mechanical shock are the failure mechanisms which can cause leakage of electrolyte from battery.
Failure effect | Failure mode | Mechanism |
|---|---|---|
Switch fails | – Contacts broken | – Mechanical damage |
– High-contact resistance | – Corrosion of contacts | |
Lamp fails to light | – Lamp filament broken | – Material defect, excess voltage |
– Lamp glass broken | – Mechanical shock | |
– Loose contact with socket | – Human error, socket defects | |
– Socket contacts damaged | – Human error, socket defects | |
Low voltage from battery | – Leakage of electrolyte | – Defective casing |
– Contacts broken | – Mechanical shock | |
Open circuit | – Wire broken | – Mechanical shock, human error |
– Wire burnt | – Short circuit, excessive current |
Lamp System Failure Analysis
The middle column, “system failure modes” constitutes the “top event” that the system analyst has to explore. In fault tree methodology, one of these is selected and the immediate preceding causes of this in column 3 are explored. These immediate causes will constitute the top events for the subsystem being examined which will then be used to extend the analysis to the chosen subsystems to form the next layer of the fault tree [4]. Consider the toy example of left middle cerebral artery occlusion leading to ischemic stroke. For this example, failure effect is global aphasia (a failure effect which will be classified as severe), failure mode is thrombotic occlusion of the left middle cerebral artery. Failure mechanism could be left carotid atherosclerosis, cardiac embolism, traumatic dissection, vasculitis, and other rare causes of stroke. Working backwards from failure modes to failure mechanisms allows for rigorous examination of the causes of thrombotic stroke.
The system analyst first defines his system and establishes boundaries. He then selects a particular system failure mode as the “top event” for further analysis. The system analyst then determines the “immediate, necessary, and sufficient” causes for the occurrence of this top event. These are not the basic causes, but the immediate causes of mechanisms of this event. Once the immediate, necessary, and sufficient causes of the global top event are determined, these in turn are considered the subtop events and the analyst proceeds onto determine the immediate, necessary, and sufficient causes of these. The analysis proceeds by switching back and forth between failure mechanisms and failure modes i.e., the “mechanism” for a system are the modes for the subsystem. Thinking in immediate, necessary, and sufficient steps is an extremely important principle called the “Think Small” rule. This proceeds till the desired limit of resolution is reached [4].
The construction of fault trees follows some basic rules [1, 4, 5]. These are:
1.
State the undesired top level event in a clear, concise statement. This should be clarified precisely as to what it is and when it occurs.
2.
Develop the upper and intermediate tiers of the fault tree; determine the intermediate failures and combinations which are immediate, necessary, and sufficient to cause the top level events and interconnect them by the appropriate logic symbols [1, 4]. Extend each fault event to the next lower level. At each level of tree construction, particular attention is paid to the following:
Can any single failures cause the event to happen?
Are multiple failure combinations necessary for the event to happen?
3.
Develop each fault tree event through more detailed levels of system design till the limit of resolution is reached and a root cause(s) is established. Root cause analysis is explored further as a management method in Chap. 8.
4.
Evaluate the fault tree in qualitative and/or quantitative terms. Fault trees are qualitative by nature of their construction. Establish probability of failure for individual components; evaluate ability of the system to meet safety margins. If safety objectives are unmet, redesign the system and reiterate the process.
Two other procedural rules are complete the Gate rule and No-Gate-to-Gate rule. The complete the Gate rule states that all inputs to a particular gate should be completely defined before further analysis of any of the inputs is undertaken. The No-Gate-to-Gate rule states that gate inputs should be well defined gate events and the outputs of individual gates should not be connected to other gates. Once the root cause(s) are identified, the investigator must be able to reconstruct the top event by traversing up the tree. As discussed in the appendices, the idea behind the analysis is to identify the “minimal cut set.” A “minimal cut set is the smallest combination of component failures, which, if they occur will cause the top event to happen” [1]. It follows by logical extension (see appendices for details) that if a single system failure can cause the top event to happen, then the design is not a fault tolerant system. It also helps understand why there is protection in redundancy (assuming independent failures). Consider a design made of two systems A and B, each with probability of failure of 1/1,000. Let us assume that our first design can fail if system A OR system B fails. Therefore, the probability of the undesired top event happening remains of the order of 1/1,000. Now let us assume systems A and B are used in a redundant manner and both must fail for the undesired top event to occur. Now the probability of failure becomes 1/1,000 × 1/1,000 or 1 in 1,000,000.
Basic ideas from probability are discussed in the following section. Appendices 1 and 2 contain further information on FTA and a closely related structure called DD, their construction and analysis using probability theory and Boolean algebra. The information in the appendices is useful for more mathematically inclined readers and can be safely skipped for understanding the use of FTA methodology for medical diagnosis used in the rest of this book.
Probability Basics
We explore some basic probability theory which has ubiquitous application in decision making. This section looks at a few basic rules from probability theory necessary for understanding fault trees and analyzing them. P(A) is a real number between 0 and 1 which denotes the probability of event A happening. Similarly P(B) is the probability of event B happening. A number closer to 1 denotes a higher probability; numbers closer to 0 denote low probabilities. P(A∪B) is the probability of event A or event B happening. P(A∩B) is the joint probability of events A and B happening [6].
1.
P(A∪B) = P(A) + P(B) – P(A∩B). This operation happens at the OR gate of the fault tree.
2.
P(A∩B) = P(A) · P(B∣A). This operation happens at the AND gate of the fault tree.
P(B∣A) denotes the probability of event B happening provided we know A has happened. For example, assume a box has ten pairs of socks, of which five pairs are white, three are red, and two are blue. The collection of all socks: white, blue, and red is called the universal set which denotes all possible outcomes. P(white socks) = 5/10, P(red socks) = 3/10 and P(blue socks) = 2/10. However, if we know that a colored sock was drawn from the box, we have restricted our possibilities to 5 since there are three red and two blue socks in the box which are colored. If we have this information, then the probability that a drawn pair of socks is red is P(Red Socks|Colored Socks) = 3/5. Similarly P(Blue Socks|Colored Socks) = 2/5 instead of 3/10 or 2/10 if we did not have this information.
If A and B are independent events, where the occurrence of one does not influence the occurrence of the other, P(A∩B) = P(A) · P(B). An important probabilistic method is Bayes theorem where we are interested in calculating the posterior probabilities of an event. This is a powerful method which forms the heart of many algorithms in artificial intelligence and machine learning [6].
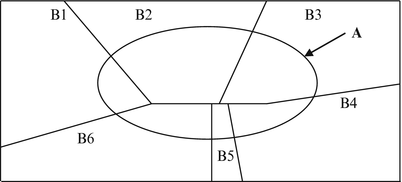
Let the universal set (rectangle in Fig. 2.3) be partitioned into six different regions. B1 + B2…B6 = Universal set. Let this be denoted by Bi where i assumes values between 1 and 6 to denote each of the six regions. There is no overlap between the partitions. For the example above, this can be expressed as:
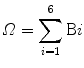
(In Eq. (2.1) the symbol ∑ denotes addition i.e., B1 + B2 + B3 + B4 + B5 + B6.)

Fig. 2.3
Bayes theorem. The rectangle represents the universal set—all possible events. It is partitioned into different regions. Given the occurrence of event A, we are interested in knowing the probability that it originated from a particular region. In the context of reliability, let B1, B2, … , B6 represent six different manufacturers of a particular component. Let A represent all defective components. If we have a particular defective component, what is the probability that it was manufactured by manufacturer B1? Bayes analysis helps estimate such probabilities [4]
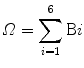
(2.1)
The event A can occur as part of the partitions of the universal set as the different regions of overlap of A and individual Bi’s demonstrate. We are interested in finding a particular Bi, given the event A has happened [4]. This can be done using Bayes rule:
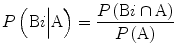
The event A can occur as part of many different partitions of the universal set. In the example in Fig. 2.3, the total probability of a defective component is the sum of individual probabilities of defectives made by different manufacturers. Therefore 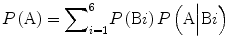 . Assume we are interested in knowing P(B2|A) or in other words the probability of a defective part made by manufacturer # 2. This is called the posterior probability [4]. Substituting the relevant terms, the corresponding posterior probability becomes:
. Assume we are interested in knowing P(B2|A) or in other words the probability of a defective part made by manufacturer # 2. This is called the posterior probability [4]. Substituting the relevant terms, the corresponding posterior probability becomes:
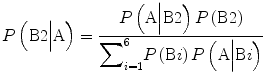
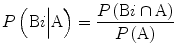
(2.2)
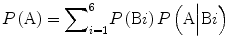 . Assume we are interested in knowing P(B2|A) or in other words the probability of a defective part made by manufacturer # 2. This is called the posterior probability [4]. Substituting the relevant terms, the corresponding posterior probability becomes:
. Assume we are interested in knowing P(B2|A) or in other words the probability of a defective part made by manufacturer # 2. This is called the posterior probability [4]. Substituting the relevant terms, the corresponding posterior probability becomes: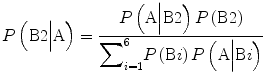
(2.3)
Toy Medical Example
To illustrate medical application of Bayes rule, consider the following example. Let the universal set be the set of patients with the following conditions: B1: CHF, B2: COPD (chronic bronchitis and emphysema), B3: Bronchial Asthma, B4: Pulmonary Embolism, B5: myasthenia gravis, and B6: Muscular Dystrophies. Let the region A denote the patients within this universal set who are short of breath. We are interested in knowing what is the probability that a patient with shortness of breath has a particular diagnosis—such as myasthenia gravis.
To make the example illustrative, let the numbers be as follows:
Total number of patients, the universal set: 100.
B1: CHF patients: 30. 30 % of whom are short of breath: 9 patients. Therefore, probability of shortness of breath given that the patient has CHF is given by P(A∣B1) = 0.3. P(B1) = 30/100 = 0.3
B2: COPD patients: 30. 50 % of whom are short of breath: 15 patients. Therefore P (A∣B2) = 0.5.
P(B2) =30/100 = 0.3
B3: Bronchial Asthma patients: 20. 20 % of whom are short of breath: 4 patients.
Therefore P(A∣B3) = 0.2. P(B3) = 0.2
B4: Pulmonary Embolism: 5 patients. 60 % of whom are short of breath: 3 patients.
Therefore P(A∣B4) = 0.6. P(B4) = 0.05
B5: Myasthenia gravis: 5 patients. 80 % of whom are short of breath: 4 patients.
Therefore P(A∣B5) = 0.80. P(B5) = 0.05
B6: Muscular Dystrophy: 10 patients. 40 % of whom are short of breath: 4 patients.
Therefore P(A∣B6) = 0.40. P(B6) = 0.1
We are interested in determining what is the probability of myasthenia gravis given that a patient is short of breath. In other words, we would like to know P(B5|A)? By application of Bayes rule from Eq. (2.3):
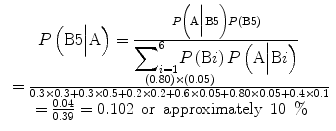 This shows that even though most patients with myasthenia gravis are short of breath (as high as 80 % in the above hypothetical example), since myasthenia is a rare disease in the population when compared with more common causes like COPD and CHF in this example, the overall posterior probability that a patient with shortness of breath has myasthenia gravis is low.
This shows that even though most patients with myasthenia gravis are short of breath (as high as 80 % in the above hypothetical example), since myasthenia is a rare disease in the population when compared with more common causes like COPD and CHF in this example, the overall posterior probability that a patient with shortness of breath has myasthenia gravis is low.
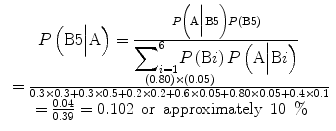
Failure Modes and Effect Analysis
FMEA is a powerful inductive analysis method. FMEA is a method of identifying the failure modes of a system or a piece-part and determining the effects on the next higher level of design [1]. It can be performed at any level within the system (function, black box, piece-part, etc.) [1]. An FMEA can be qualitative or quantitative. FMEA plays an important role in systems safety analysis and supports deductive techniques such as FTA, DD, or MA. FMEA is performed at a given level by analyzing the different ways in which a system may fail. The effect of each failure mode at a given level and the next higher level is determined. FMEA provides answers to the “What happens if ?” question [4]. The process involves assuming a certain state of function of a component or system, determining the different manners in which it can fail and determining the effect of that component on the rest of the system. The method is illustrated through the example in Fig. 2.4 [1, 4].
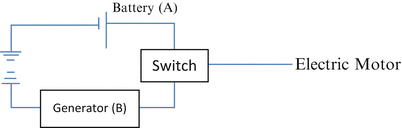

Fig. 2.4
A diesel generator (B) or battery provides electric power for operating a motor selected through a switch. The failure modes of the system are as shown in Table 2.2
The power supply system can fail in many different ways with varying degrees of impact on the system to provide electrical power to the motor. Assume that the generator is the primary power supply with the battery being the backup. A switching mechanism can switch between the generator and backup battery if the generator fails. The battery can provide limited power (for a few hours) till the generator can be restored online. Table 2.2 shows the failure modes of this system.
Component | Failure mode | Probability | Effects on motor |
|---|---|---|---|
Battery
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

|