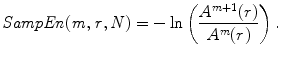is formed by the m-dimension vectors ![$$X_{i} = [u_{i},u_{i+1},\ldots,u_{i+m-1}]$$](/wp-content/uploads/2016/09/A315578_1_En_46_Chapter_IEq2.gif) and
and ![$$X_{j} = [u_{j},u_{j+1},\ldots,u_{j+m-1}]$$](/wp-content/uploads/2016/09/A315578_1_En_46_Chapter_IEq3.gif) , where
, where 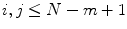 . The max distance between X i and X j can be calculated by
. The max distance between X i and X j can be calculated by
![$$\displaystyle{ d[X_{i},X_{j}] = max_{k=1,2,\ldots,m}[\vert u_{i+k-1} - u_{j+k-1}\vert ]. }$$](/wp-content/uploads/2016/09/A315578_1_En_46_Chapter_Equ1.gif)
(1)
Given a threshold r and each 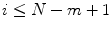 , let
, let 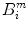 be the number of vectors X j within r of X i , and we define
be the number of vectors X j within r of X i , and we define
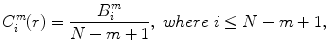
and ϕ m (r) as mean of 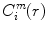
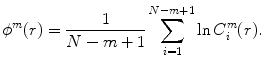
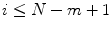 , let
, let 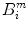 be the number of vectors X j within r of X i , and we define
be the number of vectors X j within r of X i , and we define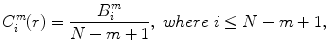
(2)
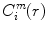
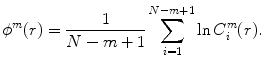
(3)
Equation (2) is mainly defined to calculate the possibility that for each Xi and Xj, the two vectors are similar within the threshold r, while Eq. (3) is used to calculate the average.
By finding ϕ m+1(r), ApEn(r, m, N) takes the form as
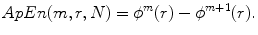
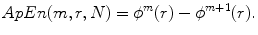
(4)
This is how ApEn is defined to measure the self-similarity of the time series [11].
2.2 Sample Entropy (SampEn)
SampEn deals with same m-dimension vectors X i and X j as defined in ApEn. The distance between two vectors is calculated by Eq. (1). In SampEn, let 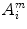 denotes the number of vectors X j within r of X i times
denotes the number of vectors X j within r of X i times 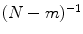 , for j ranges from 1 to
, for j ranges from 1 to 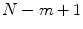 and
and 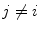 , excluding self-matches. We then define A m as mean of
, excluding self-matches. We then define A m as mean of 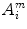 , for all
, for all 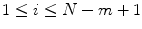 , and takes the form as
, and takes the form as
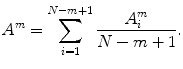
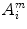 denotes the number of vectors X j within r of X i times
denotes the number of vectors X j within r of X i times 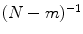 , for j ranges from 1 to
, for j ranges from 1 to 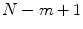 and
and 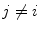 , excluding self-matches. We then define A m as mean of
, excluding self-matches. We then define A m as mean of 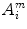 , for all
, for all 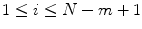 , and takes the form as
, and takes the form as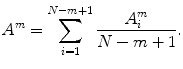
(5)
By increasing the space dimension to m + 1, and also repeat the steps in Eqs. (1) and (5), we can obtain A m+1. Then SampEn can be obtained by