as Bifurcations Shaped Through Sequential Learning

(1)

where J _ijdenotes a connection from the j-th to i-th neuron, 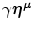$\gamma \boldsymbol{\eta ^{\mu }}$ is an input pattern 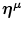$\boldsymbol{\eta ^{\mu }}$ of input strength γ, and μ is index of learned mappings. For a learned input pattern 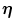$\boldsymbol{\eta }$ , we set a pattern 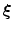$\boldsymbol{\xi }$ as a target (each pattern is a binary random pattern). The synaptic connection J _ijevolves according to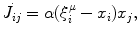

$\displaystyle{ \dot{J_{ij}} =\alpha (\xi _{i}^{\mu } - x_{ i})x_{j}, }$

(2)

where α > 0 is a learning parameter. We give a set of M random correlated input and output patterns, whose correlation satisfies $[\boldsymbol{\eta ^{\mu }}\boldsymbol{\eta ^{\mu +1}}]/N = [\boldsymbol{\xi ^{\mu }}\boldsymbol{\xi ^{\mu +1}}]/N = C$ . Here, $[\cdots \,]$ means the average over random patterns of input and target. 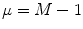Every mapping is learned in reverse numerical order from $\mu = M - 1$ to μ = 0. Further, a system learns the set iteratively in the same order.

3 Results

Through the learning process, the memories of mappings are embedded in the system. First, in order to evaluate the response of the system to the learned input, we measured the average overlap $$$[< \overline{\boldsymbol{x\xi ^{\mu }}}/N >]$$ ” src=”/wp-content/uploads/2016/09/A315578_1_En_73_Chapter_IEq8.gif”> upon η μ as a function of μ for C = 0. 9 and 0. 1, shown in Fig. 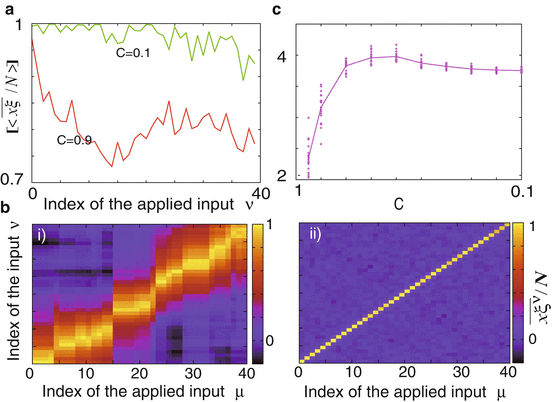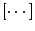<A href=$ 1a, where $\overline{\cdots \,}$ , $$$< \cdots >$$ ” src=”/wp-content/uploads/2016/09/A315578_1_En_73_Chapter_IEq10.gif”> and <IMG alt=$ mean the average over time, initial states of one network, and networks, respectively. Note that the response is defined here as an activity in the presence of an input, not as an evoked activity by a transient input used only for the initial condition as in the Hopfield model. For C = 0. 9 and 0. 1, the average overlap with the latest learned target (μ = 0) takes nearly unity and this target can be recalled perfectly. The average overlap with the earlier learned target decreases rapidly and then, saturates at around 0.8 for C = 0. 9, whereas the overlap keeps nearly unity for C = 0. 1. Interestingly, memory performance of the system that learns a set with lower correlation is greater than that with a higher correlation.

Fig. 1

(a) The average overlap $$$[< \overline{\boldsymbol{x\xi ^{\nu }}}/N >]$$ ” src=”/wp-content/uploads/2016/09/A315578_1_En_73_Chapter_IEq12.gif”> in the presence of the input ν is plotted for C = 0. 1 and 0. 9, where larger ν represents earlier learned input. (b) The average overlap <IMG alt=$ $$ ” src=”/wp-content/uploads/2016/09/A315578_1_En_73_Chapter_IEq13.gif”> with the target μ in the presence of the input ν is shown for (i) C = 0. 9 and (ii) C = 0. 1. (c) The basin entropy Σ v _ilog v _iis plotted as a function of C

Only gold members can continue reading. Log In or Register to continue