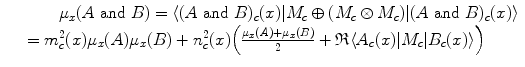which consists of two sectors: ‘sector 1’ is a Hilbert space 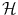 , while ‘sector 2’ is a tensor product Hilbert space
, while ‘sector 2’ is a tensor product Hilbert space 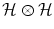 .
.
Let us now consider the membership weights of exemplars of concepts and their conjunctions/disjunctions measured by Hampton [1, 2]. He identified systematic deviations from classical set (fuzzy set) conjunctions/disjunctions, an effect known as ‘overextension’ or ‘underextension’.
Let us start from conjunctions. It can be shown that a large part of Hampton’s data cannot be modeled in a classical probability space satisfying the axioms of Kolmogorov [5]. Indeed, the membership weights 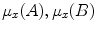 and μ x (A and B) of an exemplar x for the concepts A, B and ‘A and B’ can be represented in a classical probability model if and only if the following two conditions are satisfied (see [5] for a proof)
and μ x (A and B) of an exemplar x for the concepts A, B and ‘A and B’ can be represented in a classical probability model if and only if the following two conditions are satisfied (see [5] for a proof)
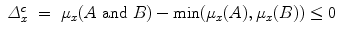
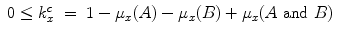
Let us consider a specific example. Hampton estimated the membership weight of Mint with respect to the concepts Food, Plant and their conjunction Food and Plant finding μ Mint (Food) = 0. 87, μ Mint (Plant) = 0. 81, μ Mint (Food and Plant) = 0. 9. Thus, the exemplar Mint presents overextension with respect to the conjunction Food and Plant of the concepts Food and Plant. We have in this case 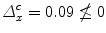 , hence no classical probability model exists for these data.
, hence no classical probability model exists for these data.
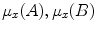 and μ x (A and B) of an exemplar x for the concepts A, B and ‘A and B’ can be represented in a classical probability model if and only if the following two conditions are satisfied (see [5] for a proof)
and μ x (A and B) of an exemplar x for the concepts A, B and ‘A and B’ can be represented in a classical probability model if and only if the following two conditions are satisfied (see [5] for a proof)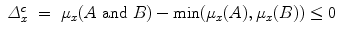
(1)
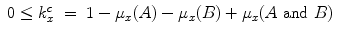
(2)
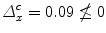 , hence no classical probability model exists for these data.
, hence no classical probability model exists for these data.Let us now come to disjunctions. Also in this case, a large part of Hampton’s data [2] cannot be modeled in a classical Kolmogorovian probability space, due to the following theorem. The membership weights μ x (A), μ x (B) and μ x (A or B) of an exemplar x for the concepts A, B and ‘A or B’ can be represented in a classical probability model if and only if the following two conditions are satisfied (see [5] for a proof)
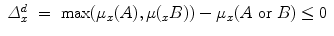
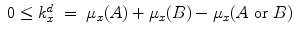
Let us again consider a specific example. Hampton estimated the membership weight of Donkey with respect to the concepts Pet, Farmyard Animal and their disjunction Pet or Farmyard Animal finding μ Donkey (Pet) = 0. 5, μ Donkey (Farmyard Animal) = 0. 9, μ Donkey (Pet or Farmyard Animal) = 0. 7. Thus, the exemplar Donkey presents underextension with respect to the disjunction Pet or Farmyard Animal of the concepts Pet and Farmyard Animal. We have in this case 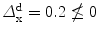 , hence no classical probability model exists for these data.
, hence no classical probability model exists for these data.
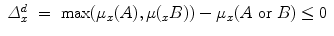
(3)
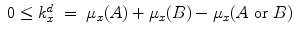
(4)
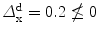 , hence no classical probability model exists for these data.
, hence no classical probability model exists for these data.It can be proved that a quantum probability model in Fock space exists for Hampton’s data, as follows [5, 12, 13].
Let us start from the conjunction of two concepts. Let x be an exemplar and let μ x (A), μ x (B), μ x (A and B) and μ x (A or B) be the membership weights of x with respect to the concepts A, B, ‘A and B’ and ‘A or B’, respectively. Let 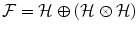 be the Fock space where we represent the conceptual entities. The concepts A, B and ‘A and B’ are represented by the unit vectors
be the Fock space where we represent the conceptual entities. The concepts A, B and ‘A and B’ are represented by the unit vectors 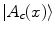 ,
, 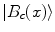 and
and 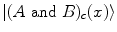 , respectively, where
, respectively, where
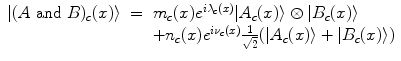
The numbers m c (x) and n c (x) are such that 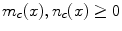 and
and 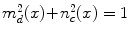 . The decision measurement of a subject who estimates the membership of the exemplar x with respect to the concept ‘A and B’ is represented by the orthogonal projection operator
. The decision measurement of a subject who estimates the membership of the exemplar x with respect to the concept ‘A and B’ is represented by the orthogonal projection operator 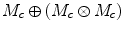 on
on 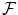 , where M c is an orthogonal projection operator on
, where M c is an orthogonal projection operator on 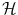 . Hence, the membership weight of x with respect to ‘A and B’ is given by
. Hence, the membership weight of x with respect to ‘A and B’ is given by
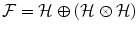 be the Fock space where we represent the conceptual entities. The concepts A, B and ‘A and B’ are represented by the unit vectors
be the Fock space where we represent the conceptual entities. The concepts A, B and ‘A and B’ are represented by the unit vectors 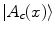 ,
, 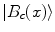 and
and 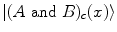 , respectively, where
, respectively, where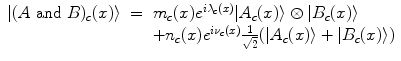
(5)
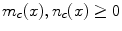 and
and 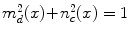 . The decision measurement of a subject who estimates the membership of the exemplar x with respect to the concept ‘A and B’ is represented by the orthogonal projection operator
. The decision measurement of a subject who estimates the membership of the exemplar x with respect to the concept ‘A and B’ is represented by the orthogonal projection operator 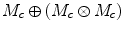 on
on 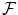 , where M c is an orthogonal projection operator on
, where M c is an orthogonal projection operator on 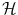 . Hence, the membership weight of x with respect to ‘A and B’ is given by
. Hence, the membership weight of x with respect to ‘A and B’ is given by