be the non-vanishing polarization density, where the charge density ρ and the (average) dipole length δ are real quantities. The charge density wave function σ(x) is
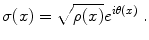
(1)
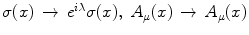 , where A μ (x) is the electromagnetic (e.m.) field and λ is space-time independent. The symmetry breakdown occurs when the charge density ρ(x) has a non vanishing expectation value in the system ground state (the vacuum)
, where A μ (x) is the electromagnetic (e.m.) field and λ is space-time independent. The symmetry breakdown occurs when the charge density ρ(x) has a non vanishing expectation value in the system ground state (the vacuum)  :
: 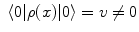 .
.The system is also invariant under the local gauge transformation
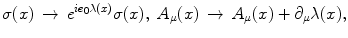
with 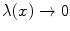 for
for 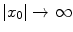 and/or
and/or 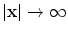 ,
, 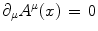 , and
, and
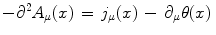
with j μ (x) denoting the current. We remark that a shift in the θ(x) phase field, i.e.
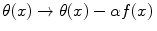
describes non-homogeneous boson condensation of the field θ(x) in the system ground state, namely the formation of coherent domains of finite size [7, 9, 10]. α is a constant, f(x), called the boson condensation function, acts as a “form factor” specific for the considered domain [7, 9, 10] and satisfies the same equation satisfied by the θ(x) field, i.e. ∂ 2 f(x) = 0.
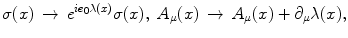
(2)
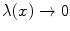 for
for 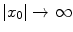 and/or
and/or 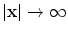 ,
, 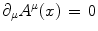 , and
, and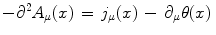
(3)
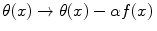
(4)
In order for the condensation process to be physically detectable, f(x) has to carry some topological singularity, it has to be path-dependent [7, 9, 10] (a regular f(x) do not produce any observable effect). However, observables are influenced by gradients, ∂ μ f(x), in the boson condensate and therefore ∂ μ f(x) has to be single-valued. The stationary function f(x) may carry a vortex singularity given by
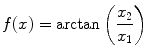
which shows that the phase is undefined on the line r = 0, with 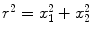 , consistently with the observed phase indeterminacy in the process of transition between two AM pattern frames. As a result of the single-valuedness of σ(x), the topological singularity is characterized by the winding number n:
, consistently with the observed phase indeterminacy in the process of transition between two AM pattern frames. As a result of the single-valuedness of σ(x), the topological singularity is characterized by the winding number n: 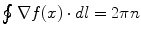 , n = 0, ±1, ±2, …, when the integration path is along the closed circle (0, 2π) (flux quantization). Phase transitions can be shown to be induced only by a singular boson transformation function f(x) [7, 9, 10]. For this reason topologically non-trivial extended objects, such as vortices, are initiated during the critical regime of phase transitions. The apex of phase cones, where vortices start to be formed, is not initiated within frames, but between frames (during phase transitions). As in observations, the initial site where non-homogeneous condensation starts (the phase cone apex) is not conditioned by the incoming stimulus, but is randomly determined by the concurrence of a number of local conditions. The non-homogeneous condensation of the phase field θ(x), out of which the vortex arises, spans (almost) the whole system since it is a (quasi-)massless field. This is why in its life-time the vortex is observed to occupy the whole area of the phase-locked neural activity of the cortex.
, n = 0, ±1, ±2, …, when the integration path is along the closed circle (0, 2π) (flux quantization). Phase transitions can be shown to be induced only by a singular boson transformation function f(x) [7, 9, 10]. For this reason topologically non-trivial extended objects, such as vortices, are initiated during the critical regime of phase transitions. The apex of phase cones, where vortices start to be formed, is not initiated within frames, but between frames (during phase transitions). As in observations, the initial site where non-homogeneous condensation starts (the phase cone apex) is not conditioned by the incoming stimulus, but is randomly determined by the concurrence of a number of local conditions. The non-homogeneous condensation of the phase field θ(x), out of which the vortex arises, spans (almost) the whole system since it is a (quasi-)massless field. This is why in its life-time the vortex is observed to occupy the whole area of the phase-locked neural activity of the cortex.
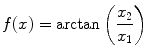
(5)
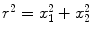 , consistently with the observed phase indeterminacy in the process of transition between two AM pattern frames. As a result of the single-valuedness of σ(x), the topological singularity is characterized by the winding number n:
, consistently with the observed phase indeterminacy in the process of transition between two AM pattern frames. As a result of the single-valuedness of σ(x), the topological singularity is characterized by the winding number n: 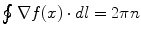 , n = 0, ±1, ±2, …, when the integration path is along the closed circle (0, 2π) (flux quantization). Phase transitions can be shown to be induced only by a singular boson transformation function f(x) [7, 9, 10]. For this reason topologically non-trivial extended objects, such as vortices, are initiated during the critical regime of phase transitions. The apex of phase cones, where vortices start to be formed, is not initiated within frames, but between frames (during phase transitions). As in observations, the initial site where non-homogeneous condensation starts (the phase cone apex) is not conditioned by the incoming stimulus, but is randomly determined by the concurrence of a number of local conditions. The non-homogeneous condensation of the phase field θ(x), out of which the vortex arises, spans (almost) the whole system since it is a (quasi-)massless field. This is why in its life-time the vortex is observed to occupy the whole area of the phase-locked neural activity of the cortex.
, n = 0, ±1, ±2, …, when the integration path is along the closed circle (0, 2π) (flux quantization). Phase transitions can be shown to be induced only by a singular boson transformation function f(x) [7, 9, 10]. For this reason topologically non-trivial extended objects, such as vortices, are initiated during the critical regime of phase transitions. The apex of phase cones, where vortices start to be formed, is not initiated within frames, but between frames (during phase transitions). As in observations, the initial site where non-homogeneous condensation starts (the phase cone apex) is not conditioned by the incoming stimulus, but is randomly determined by the concurrence of a number of local conditions. The non-homogeneous condensation of the phase field θ(x), out of which the vortex arises, spans (almost) the whole system since it is a (quasi-)massless field. This is why in its life-time the vortex is observed to occupy the whole area of the phase-locked neural activity of the cortex.The null spike appearing in the critical regime acts as a shutter that blanks the intrinsic background ECoG. When the order parameter goes to zero the microscopic activity does not decrease, but, as the model predicts, it becomes disordered, unstructured (fully symmetric). At very low analytic amplitude, the analytic phase is undefined, as it is indeed at the vortex core, and, under the incoming weak sensory input, the background activity may re-set in a new AM frame, if any, formed by reorganizing the existing activity, not by driving it by input (except for the small energy provided by the stimulus that is required to selectively excite a Hebbian nerve cell assembly needed to force the phase transition). As in the observations, in the model the reduction in activity constitutes a singularity in the dynamics at which the phase is undefined. The aperiodic shutter allows opportunities for phase transitions.
The model predicts converging (imploding) and diverging (exploding) regimes [7]. Many phase cones show little or no rotation but repetitive outward or inward pulsations with each cycle [8]. The singularity of to their rotational gradients (vortices) is associated to the one of the vortex core. The model explains all four types of these observed spatiotemporal phase gradients. The negative gradient could be explained in conventional neurodynamics (e.g. in terms of a pacemaker), but not the positive gradient. There is no explanation in the conventional framework of why both gradients, the positive and the negative one, occur, one or the other at random.
3 Brain Dark Energy
The neural mechanism of perception depends on repeated transfer of mesoscopic energy to microscopic energy and vice-versa, as the basis for the disintegration of a mesoscopic AM pattern and the formation of a new one, respectively. Provided changes in the inverse temperature β are slow, as it actually happens in mammalian brains which keep their temperature nearly constant, these energy transfers are controlled by the time derivative of the number N of the NG field condensate [6, 7]:
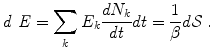
E k and 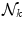 are the energy and the number of the NG excitations of momentum k. Equation (6) relates the changes in the energy
are the energy and the number of the NG excitations of momentum k. Equation (6) relates the changes in the energy 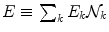 and entropy
and entropy 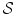 implied by the minimization of the free energy
implied by the minimization of the free energy 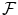 at any t,
at any t, 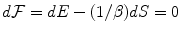 . Through the changes in time of the NG condensate, the entropy changes and heat dissipation,
. Through the changes in time of the NG condensate, the entropy changes and heat dissipation, 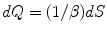 , involved in the disappearance/emergence of the coherence (ordering) associated to the AM patterns, turns into energy changes. Heat dissipation is indeed a significant variable in laboratory observations. Brains require constant perfusion with arterial blood and venous removal to dispose of substantial waste heat.
, involved in the disappearance/emergence of the coherence (ordering) associated to the AM patterns, turns into energy changes. Heat dissipation is indeed a significant variable in laboratory observations. Brains require constant perfusion with arterial blood and venous removal to dispose of substantial waste heat.
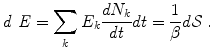
(6)
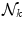 are the energy and the number of the NG excitations of momentum k. Equation (6) relates the changes in the energy
are the energy and the number of the NG excitations of momentum k. Equation (6) relates the changes in the energy 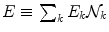 and entropy
and entropy 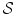 implied by the minimization of the free energy
implied by the minimization of the free energy 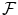 at any t,
at any t, 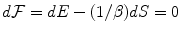 . Through the changes in time of the NG condensate, the entropy changes and heat dissipation,
. Through the changes in time of the NG condensate, the entropy changes and heat dissipation, 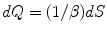 , involved in the disappearance/emergence of the coherence (ordering) associated to the AM patterns, turns into energy changes. Heat dissipation is indeed a significant variable in laboratory observations. Brains require constant perfusion with arterial blood and venous removal to dispose of substantial waste heat.
, involved in the disappearance/emergence of the coherence (ordering) associated to the AM patterns, turns into energy changes. Heat dissipation is indeed a significant variable in laboratory observations. Brains require constant perfusion with arterial blood and venous removal to dispose of substantial waste heat.Let 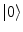 and
and 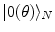 denote (see Refs. [4, 6, 7] for details) the states of the brain activity corresponding to the absence of NG quanta describing the long range neuronal correlations A k and
denote (see Refs. [4, 6, 7] for details) the states of the brain activity corresponding to the absence of NG quanta describing the long range neuronal correlations A k and 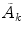 (
(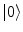 is “the vacuum”) and the condensate state of condensation density
is “the vacuum”) and the condensate state of condensation density 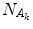 (and
(and 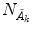 ), respectively. The inner products of these states is given by:
), respectively. The inner products of these states is given by: 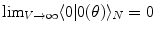 and
and 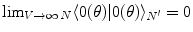 , for any N and any
, for any N and any 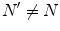 . These relations signal that in the limit of infinitely many degrees of freedom the process of condensation of the A and
. These relations signal that in the limit of infinitely many degrees of freedom the process of condensation of the A and 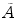 modes is a phase transition process: the states
modes is a phase transition process: the states 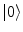 and
and 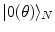 , for any N, represent ‘distinct’ phases of the brain activity since no overlap exist among them for different values of N. These relations also express the criticality present in the brain background activity since their meaning is that no unitary transformation exists able to lead from one phase coded by N to another phase coded by N ′ , with
, for any N, represent ‘distinct’ phases of the brain activity since no overlap exist among them for different values of N. These relations also express the criticality present in the brain background activity since their meaning is that no unitary transformation exists able to lead from one phase coded by N to another phase coded by N ′ , with 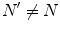 : they are ‘unitarily inequivalent phases’ and transitions from phase to phase are critical transition processes. The non-equilibrium dynamics has been studied in detail by use of the Ginzburg–Landau (GL) time dependent equation in [11]. For any
: they are ‘unitarily inequivalent phases’ and transitions from phase to phase are critical transition processes. The non-equilibrium dynamics has been studied in detail by use of the Ginzburg–Landau (GL) time dependent equation in [11]. For any 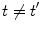 it is
it is 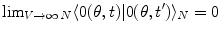 , which shows that brain activity is far from the equilibrium and characterized by criticality at any time t, indeed. Time evolution of the phase coded by N appears to be a far from the equilibrium critical process (
, which shows that brain activity is far from the equilibrium and characterized by criticality at any time t, indeed. Time evolution of the phase coded by N appears to be a far from the equilibrium critical process (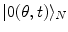 and
and 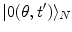 are unitarily inequivalent phases). In the non-stationary regime, the non-vanishing dF expresses the rate at which the system approaches the stationary regime at the minimum of the free energy. In [11] it is shown that the rate of change of the condensate d N A ∕dt in the non-stationary regime, named the critical GL regime, is proportional to the relaxation term
are unitarily inequivalent phases). In the non-stationary regime, the non-vanishing dF expresses the rate at which the system approaches the stationary regime at the minimum of the free energy. In [11] it is shown that the rate of change of the condensate d N A ∕dt in the non-stationary regime, named the critical GL regime, is proportional to the relaxation term 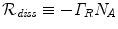 , with the ‘damping’
, with the ‘damping’ 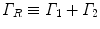 , where Γ 1 depends on the diffusion coefficient
, where Γ 1 depends on the diffusion coefficient 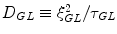 , (ξ GL and τ GL are the GL correlation length and the GL relaxation life-time, respectively). Γ 2 depends on non-homogeneities.
, (ξ GL and τ GL are the GL correlation length and the GL relaxation life-time, respectively). Γ 2 depends on non-homogeneities.
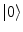 and
and 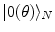 denote (see Refs. [4, 6, 7] for details) the states of the brain activity corresponding to the absence of NG quanta describing the long range neuronal correlations A k and
denote (see Refs. [4, 6, 7] for details) the states of the brain activity corresponding to the absence of NG quanta describing the long range neuronal correlations A k and 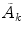 (
(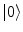 is “the vacuum”) and the condensate state of condensation density
is “the vacuum”) and the condensate state of condensation density 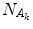 (and
(and 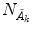 ), respectively. The inner products of these states is given by:
), respectively. The inner products of these states is given by: 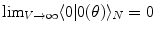 and
and 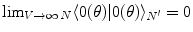 , for any N and any
, for any N and any 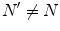 . These relations signal that in the limit of infinitely many degrees of freedom the process of condensation of the A and
. These relations signal that in the limit of infinitely many degrees of freedom the process of condensation of the A and 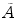 modes is a phase transition process: the states
modes is a phase transition process: the states 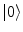 and
and 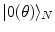 , for any N, represent ‘distinct’ phases of the brain activity since no overlap exist among them for different values of N. These relations also express the criticality present in the brain background activity since their meaning is that no unitary transformation exists able to lead from one phase coded by N to another phase coded by N ′ , with
, for any N, represent ‘distinct’ phases of the brain activity since no overlap exist among them for different values of N. These relations also express the criticality present in the brain background activity since their meaning is that no unitary transformation exists able to lead from one phase coded by N to another phase coded by N ′ , with 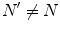 : they are ‘unitarily inequivalent phases’ and transitions from phase to phase are critical transition processes. The non-equilibrium dynamics has been studied in detail by use of the Ginzburg–Landau (GL) time dependent equation in [11]. For any
: they are ‘unitarily inequivalent phases’ and transitions from phase to phase are critical transition processes. The non-equilibrium dynamics has been studied in detail by use of the Ginzburg–Landau (GL) time dependent equation in [11]. For any 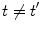 it is
it is 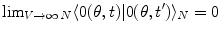 , which shows that brain activity is far from the equilibrium and characterized by criticality at any time t, indeed. Time evolution of the phase coded by N appears to be a far from the equilibrium critical process (
, which shows that brain activity is far from the equilibrium and characterized by criticality at any time t, indeed. Time evolution of the phase coded by N appears to be a far from the equilibrium critical process (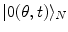 and
and 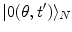 are unitarily inequivalent phases). In the non-stationary regime, the non-vanishing dF expresses the rate at which the system approaches the stationary regime at the minimum of the free energy. In [11] it is shown that the rate of change of the condensate d N A ∕dt in the non-stationary regime, named the critical GL regime, is proportional to the relaxation term
are unitarily inequivalent phases). In the non-stationary regime, the non-vanishing dF expresses the rate at which the system approaches the stationary regime at the minimum of the free energy. In [11] it is shown that the rate of change of the condensate d N A ∕dt in the non-stationary regime, named the critical GL regime, is proportional to the relaxation term 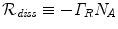 , with the ‘damping’
, with the ‘damping’ 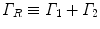 , where Γ 1 depends on the diffusion coefficient
, where Γ 1 depends on the diffusion coefficient 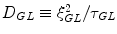 , (ξ GL and τ GL are the GL correlation length and the GL relaxation life-time, respectively). Γ 2 depends on non-homogeneities.
, (ξ GL and τ GL are the GL correlation length and the GL relaxation life-time, respectively). Γ 2 depends on non-homogeneities.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree






