Fig. 1
Outline of the general procedure for pattern detection. (a) Three cells, labeled A, B, and C, participate to a patterned activity. Three occurrences of two precise patterns are detected. Each occurrence of the first pattern has been labeled by a specific marker in order to help the reader to identify the corresponding spikes. (b) Estimation of the statistical significance of the detected patterns. Two patterns, n = 2, < A,C,B > and < C,C,C > were found. Each pattern was formed by three neurons, c = 3, and was repeated three times, r = 3, in the analyzed record. The expected number of patterns of this complexity and repetition number was N = 0.04. The probability to observe 2 or more patterns when 0.04 patterns are expected is noted as pr{0.02, 4}. (c) Display of the pattern occurrences as a raster plot aligned on the patterns’ start (Adapted from [19])
2 Dynamical System Analysis
The brain is characterized by biochemical reactions whose energy requirement is derived almost entirely from glucose consumption coupled with processes intended to transmit and integrate the information carried by the spikes across the neural networks. For sake of simplicity it is rationale to describe the activity of the neural network with the spike trains of all its elements. Spike trains are statistically expressed by point-like processes with the meaning that point process system are systems whose input and output are point processes. In a dynamical system the subsequent state of the system is determined by its present state. The irreversible dissipative processes associated to brain metabolism introduce an essential metastability of brain dynamics. A dynamical system in a whole is said to be deterministic if it is possible to predict precisely the evolution of the system in time if one knows exactly the initial conditions and the subsequent perturbations. However, a slight change or incorrect measurement in these values results in a seemingly unpredictable evolution of the system. A passage in time of a state defines a process. Whenever a process is completely deterministic at each step of its temporal evolution but unpredictable over the long term it is called a chaotic process or simply chaos.
An equivalent definition of a process is a path over time, or trajectory, in the space of states. The points approached by the trajectory as the time increases to infinity are called fixed points and the set of these points forms an attractor. If the evolution in time of the system is described by a trajectory forming a closed loop also referred to as a periodic orbit then the system is said to have a limit cycle. It is unlikely that the irreversible dissipative processes associated with brain dynamics produces always the same repeating sequence of states. However, this aperiodic behavior is different from randomness, or stochastic process, because an iterated value of the point process (all spike trains in the network) can only occur once in the series, otherwise due to the deterministic dynamics of the system the next value should also be a repetition and so on for all subsequent values. The perturbations applied to any combination of the governing set of parameters move a dynamical system characterized by fixed points away from the periodic orbits but with passing of time the trajectory collapses asymptotically to the same attractor. If the system is deterministic, yet sensitive to small perturbations, the trajectory defining its dynamics is an aperiodic orbit, then the system is said to have a chaotic attractor, often referred to as a strange attractor. Then, the set of all possible perturbations define the inset of the attractor or its basin of attraction.
By extending this approach to the spike trains recorded from all elements of the neural network it is theoretically possible to develop an acceptable model for the identification of the system. Notice that the goodness of fit of a certain kernel estimate as plausible is evaluated by means of a function f describing its mode of activity–the mode of activity being defined by how an information is processed within a neural network and how it is associated to the output pattern of activity that is generated. In formal terms f is a probability function that describes how a state x is mapped into the space of states. If the function is set by a control parameter μ we can write f μ (x) = f(μ, x). A dynamical system x ′ is a subset of the space of states and can be obtained by taking the gradient of the probability function with respect to the state variable, that is 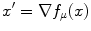 . Mathematically speaking, the space of states is a finite dimensional smooth manifold assuming that f is continuously differentiable and the system has a finite number of degrees of freedom [18].
. Mathematically speaking, the space of states is a finite dimensional smooth manifold assuming that f is continuously differentiable and the system has a finite number of degrees of freedom [18].
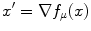 . Mathematically speaking, the space of states is a finite dimensional smooth manifold assuming that f is continuously differentiable and the system has a finite number of degrees of freedom [18].
. Mathematically speaking, the space of states is a finite dimensional smooth manifold assuming that f is continuously differentiable and the system has a finite number of degrees of freedom [18].If the activity is generated by chaotic attractors, whose trajectories are not represented by a limit set either before or after the perturbations, the attracting set may be viewed through the geometry of the topological manifold in which the trajectories mix. It is likely that several attractors may appear, moving in space and time across different areas of the network, in the dynamics of large neural networks. Such complex spatio-temporal activity may be viewed more generally as an attracting state, instead of simply an attractor [3]. In particular, simulation studies demonstrated that a neural circuit activated by the same initial pattern tends to stabilize into a timely organized mode or in a asynchronous mode if the excitability of the circuit elements is adjusted to the first order kinetics of the postsynaptic potentials [10, 22].
3 The Brain Catastrophe
Let us assume that the dynamical system is structurally stable. In terms of topology structural stability means that for a dynamical system x ′ it exists a neighborhood 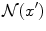 in the space of states with the property that every
in the space of states with the property that every 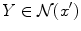 is topologically equivalent to x ′ . This assumption is extremely important because a structurally stable dynamical system cannot degenerate. As a consequence, there is no need to know the exact equations of the dynamical system because qualitative, approximate equations, i.e. in the neighborhood, show the same qualitative behavior [2]. In the case of two control parameters,
is topologically equivalent to x ′ . This assumption is extremely important because a structurally stable dynamical system cannot degenerate. As a consequence, there is no need to know the exact equations of the dynamical system because qualitative, approximate equations, i.e. in the neighborhood, show the same qualitative behavior [2]. In the case of two control parameters, 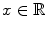 ,
, 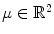 , the probability function f is defined as the points μ of
, the probability function f is defined as the points μ of 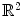 with a structurally stable dynamics of
with a structurally stable dynamics of 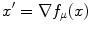 [15]. That means the qualitative dynamics x ′ is defined in a neighborhood of a pair (x 0, μ 0) at which f is in equilibrium (e.g. minima, maxima, saddle point). With these assumptions, the equilibrium surface is geometrically equivalent to the Riemann-Hugoniot or cusp catastrophe [20]. The cusp catastrophe is the universal unfolding of the singularity f(x) = x 4 and the equilibrium surface is described by the equation
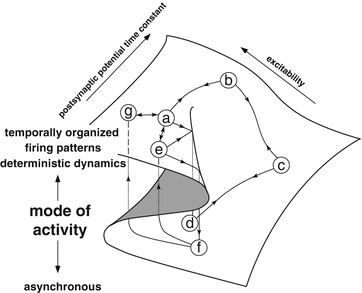
[15]. That means the qualitative dynamics x ′ is defined in a neighborhood of a pair (x 0, μ 0) at which f is in equilibrium (e.g. minima, maxima, saddle point). With these assumptions, the equilibrium surface is geometrically equivalent to the Riemann-Hugoniot or cusp catastrophe [20]. The cusp catastrophe is the universal unfolding of the singularity f(x) = x 4 and the equilibrium surface is described by the equation 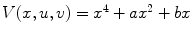 , where a and b are the control parameters. We suggest that metastable modes of neural activity could lie in the equilibrium surface with postsynaptic potential kinetics and membrane excitability as control parameters (Fig. 2).
, where a and b are the control parameters. We suggest that metastable modes of neural activity could lie in the equilibrium surface with postsynaptic potential kinetics and membrane excitability as control parameters (Fig. 2).
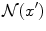 in the space of states with the property that every
in the space of states with the property that every 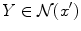 is topologically equivalent to x ′ . This assumption is extremely important because a structurally stable dynamical system cannot degenerate. As a consequence, there is no need to know the exact equations of the dynamical system because qualitative, approximate equations, i.e. in the neighborhood, show the same qualitative behavior [2]. In the case of two control parameters,
is topologically equivalent to x ′ . This assumption is extremely important because a structurally stable dynamical system cannot degenerate. As a consequence, there is no need to know the exact equations of the dynamical system because qualitative, approximate equations, i.e. in the neighborhood, show the same qualitative behavior [2]. In the case of two control parameters, 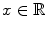 ,
, 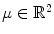 , the probability function f is defined as the points μ of
, the probability function f is defined as the points μ of 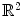 with a structurally stable dynamics of
with a structurally stable dynamics of 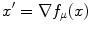 [15]. That means the qualitative dynamics x ′ is defined in a neighborhood of a pair (x 0, μ 0) at which f is in equilibrium (e.g. minima, maxima, saddle point). With these assumptions, the equilibrium surface is geometrically equivalent to the Riemann-Hugoniot or cusp catastrophe [20]. The cusp catastrophe is the universal unfolding of the singularity f(x) = x 4 and the equilibrium surface is described by the equation
[15]. That means the qualitative dynamics x ′ is defined in a neighborhood of a pair (x 0, μ 0) at which f is in equilibrium (e.g. minima, maxima, saddle point). With these assumptions, the equilibrium surface is geometrically equivalent to the Riemann-Hugoniot or cusp catastrophe [20]. The cusp catastrophe is the universal unfolding of the singularity f(x) = x 4 and the equilibrium surface is described by the equation 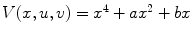 , where a and b are the control parameters. We suggest that metastable modes of neural activity could lie in the equilibrium surface with postsynaptic potential kinetics and membrane excitability as control parameters (Fig. 2).
, where a and b are the control parameters. We suggest that metastable modes of neural activity could lie in the equilibrium surface with postsynaptic potential kinetics and membrane excitability as control parameters (Fig. 2).