Fig. 1
Our arm model in Euler angle scheme
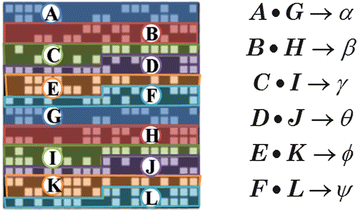
Fig. 2
Firing pattern of 400 neurons & sub-vectors’ codings which correspond to incremental motions via Euler angles
2 Method and Model
Our study works with an interconnected recurrent neural network model (abbreviated as RNNM hereafter) consisting of N binary neurons, and the updating rule is defined by
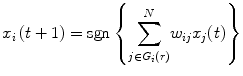
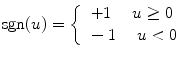 where x i (t) = ±1 (i =1 ∼ N) is the firing state of a neuron specified by space site index i at time t, and w ij is connection weight from the neuron x j to the neuron x i . w ii is taken to be 0. r (0 < r < N) is fan-in number for neuron x i , named connectivity that is the most important system parameter in our work. G i (r) is a spatial configuration set of connectivity r for neuron x i., the number of which are N−1C r . Therefore, with full connectivity r = N − 1, determination of w ij by means of a kind of orthogonalized learning method enables us to embed a group of N dimensional state patterns (vectors) as cycle memory attractors in N dimensional state space. Let us employ our arm model as shown in Fig. 1, and introduce coding of sub-vectors of neuron firing pattern (vector) as increment of the Euler angles in arm motion. In our neural model system, attractor patterns consists of (K patterns per cycle) × L cycles, and each patterns has N neurons. In this work, we take K = 4, L = 8, and N = 400, where the firing states of N = 20 × 20 = 400 neurons are represented by black pixel or white pixel (see Fig. 2). Long time updating makes an initial pattern converge to one of the embedded cycle attractors.
where x i (t) = ±1 (i =1 ∼ N) is the firing state of a neuron specified by space site index i at time t, and w ij is connection weight from the neuron x j to the neuron x i . w ii is taken to be 0. r (0 < r < N) is fan-in number for neuron x i , named connectivity that is the most important system parameter in our work. G i (r) is a spatial configuration set of connectivity r for neuron x i., the number of which are N−1C r . Therefore, with full connectivity r = N − 1, determination of w ij by means of a kind of orthogonalized learning method enables us to embed a group of N dimensional state patterns (vectors) as cycle memory attractors in N dimensional state space. Let us employ our arm model as shown in Fig. 1, and introduce coding of sub-vectors of neuron firing pattern (vector) as increment of the Euler angles in arm motion. In our neural model system, attractor patterns consists of (K patterns per cycle) × L cycles, and each patterns has N neurons. In this work, we take K = 4, L = 8, and N = 400, where the firing states of N = 20 × 20 = 400 neurons are represented by black pixel or white pixel (see Fig. 2). Long time updating makes an initial pattern converge to one of the embedded cycle attractors.
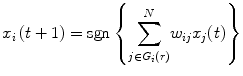
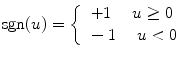
Now, when we reduce connectivity r by blocking signal transfer from the other neurons, then attractors gradually become unstable, and the network state changes from attractor dynamics to chaotic dynamics, where we discard the detailed description of the destabilizing processes [5]. Let us describe actual arm motions and neural firing patterns (vectors). In the full connection state, when one of the embedded cycle attractors appears, then, at each time step, decoded quantities following the corresponding relations shown in Fig. 2 stationary give incremental Euler angles, so the generated motion by them is one of the definite motions shown in Fig. 4, whereas they are snap shots of the definite periodic motions of arm. It should be noted that, to display the results of computer experiment, we used the software “Insilico IDE” which is opened to the public on the web site “Physiome Platform”. Once connectivity is reduced to one order of magnitude smaller than full connection number, then dynamics of firing pattern becomes chaotic. Correspondingly, decoded motions indicate chaotic behaviors, in which fragmental motion of the embedded definite motions are coming out, vanishing, coming out vanishing, and repeating them chaotically.








