(1)
Department of Neurology, Wake Forest University School of Medicine, Winston-Salem, NC, USA
Abstract
This chapter extends probabilistic analytical methods introduced in Chap. 2. The principle of transformation of medical information into data visualization is introduced in this chapter. This enables transforming a diverse array of clinical problems into simple, standard forms which lend themselves more easily to diagnostic solutions. Data distillation followed by data visualization allows clinical problems to be formulated into decision making “nodes” which lend themselves to graphical methods of problem solving. This method is exploited widely in computer science and forms the basis for many optimization algorithms used ubiquitously. Candidate diagnosis, differential diagnosis can be selected and evaluated probabilistically. Like Fault Tree Analysis, these methods can be qualitative and quantitative. Illustrative case examples are provided following introduction of the theoretical fundamentals.
Keywords
Machine learningData distillationData visualizationGraphical modelsNodesEdgesBayesian methodsSensory ataxic neuropathy with dysarthria and ophthalmoparesis (SANDO)Paraneoplastic syndromePolyneuropathy organomegaly endocrinopathy M spike and skin changes (POEMS) syndromeMedical Problem Solving: The Computer Science Perspective
In this chapter we explore principles from computer science that can help with medical problem solving. Machine learning refers to a branch of computer science which involves learning from data and making decisions [1]. At their heart, many algorithms in machine learning can be understood to be forms of mathematical optimization. Frequently, this involves defining and solving a “cost function” such that the best solution to the problem minimizes the error between the predicted solution and the real solution [1].
Certain cost functions lend themselves well to standard solutions. Therefore, a lot of machine learning involves transforming diverse problems into a few standard forms and then obtaining solutions to the transformed problem. Basic probability principles developed in Chap. 2 are used in this chapter.
One of the most famous optimization algorithms in computer science is the traveling salesman problem (TSP). Given a list of cities and distances between pairs of cities, what is the shortest route that visits each city only once and returns to the original city [2]? Many different problems in the real world can be transformed into the TSP and the same solution method applied. Examples include vehicle routing for logistics companies, designing electronic circuit boards where the cities represent locations of different electronic components which need to be placed and linked together. Once the problem is converted into standard form (such as the TSP), the solution approach remains the same, despite a vastly different application.
While machine learning attempts to create intelligence in computers modeled along human lines, this chapter travels in the reverse direction. Can applying machine learning methods help with diagnosis? Can physicians think like computers or formulate problems like computers and work it out on pen and paper? I will present some case examples of successful results from formulating challenging diagnostic problems along computer science lines. Such research is already underway at many research centers, the interested reader is encouraged to study IBM “Watson” [3] for more information [4].
The main idea with medical diagnosis is to go from manifestations of disease-termed symptoms to the underlying condition that produced them. The challenge lies in the fact that the mapping between disease and symptoms is many to one, i.e., many diseases look alike in terms of symptoms. For example tumors, strokes, dementias, nerve disease, and muscle disease can all produce the symptom of swallowing difficulty or slurring of speech. The diagnostic tests depend on the physician’s a-priori thought and judgment—tumors and strokes are best diagnosed with an MRI Brain with contrast while nerve and muscle diseases are best diagnosed with blood tests for diseases such as myasthenia gravis and nerve conduction/EMG tests. Since these tests are very expensive (several thousand dollars and restricted in resource availability), initial problem formulation is exceedingly important for avoiding wasteful testing and making timely diagnosis.
Discovering the relationship between manifest data and underlying processes (which are hidden) that generate them forms the basis of statistical inference. Such methods are in use every day for numerous real-world applications. For example, based on observed temperature, wind, cloud data, a prediction can be made about whether the weather will be stormy, clear, etc. Speech recognition is another example. In this instance, statistical inference maps the observed pattern of sound changes to the underlying word that was spoken. Hidden Markov Models (HMM), form the basis of many speech recognition algorithms [1]. Neural networks, support vector machines are other powerful algorithms which are commonly used. A detailed discussion of all such techniques is beyond the scope of this chapter. The interested reader is directed to an excellent textbook by Trevor Hastie et al. for further information [1].
These techniques are highly data and computation intense. However, the abstract algorithmic principles behind them can be applied to individual problem solving and often can help the investigator form a solution. This section will demonstrate case examples of applications of graph theoretical methods which facilitate problem solving once a problem has been expressed graphically. The main advantage with this method is that it helps with data visualization and representation. Data visualization is a very powerful tool for conceptual understanding of a problem and helps with solutions planning. The clinician can build various hypotheses connecting different symptoms (observed random variables in statistical parlance) in parallel, assigning different degrees of belief to each hypothesis (possible diagnosis) for investigation in parallel. A special type of graph theoretical model called Bayesian network is a powerful tool for analyzing such problems where probabilities can be assigned between symptoms and a disease hypothesis where a relationship between the two can be postulated to exist. For the example in Fig. 5.1, the symptom is slurring of speech and one of the possible diagnostic hypotheses is “myasthenia gravis”.
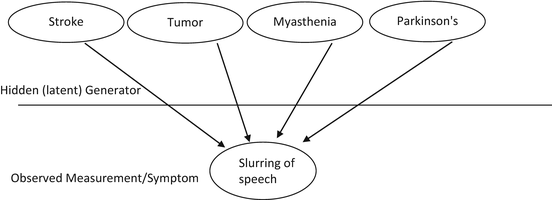

Fig. 5.1
The many to one mapping from underlying diseases to manifestations of disease (symptoms)
First, a quick introduction to graph theory and Bayesian networks. Graph theory is the study of graphs. A graph is a collection of vertices or nodes and connections between them when a relation exists between any pair of vertices called edges [1, 4]. An example of this in day-to-day life would be a road map with nodes being cities and edges being the highways connecting a pair of cities. Directed graphs have edges where direction is important, such as a one-way street that connects two cities where cars can go only in one direction and not the other. Quantification in this simple model can be attained by assigning distance or travel times between cities to give an idea about the strength of a connection between any city pair.
Combining graph theory with probability theory leads to a structure called Bayesian Network (BN). Bayesian networks are also called belief networks. They belong to the family of probabilistic graphical models where observed random variables (example: symptoms such as fever, headache, etc. for applications in medicine) are represented as nodes of a graph and the probability of co-occurrence of a pair of random variables can be encoded by an edge. It is a powerful tool for visualizing and understanding data and has broad applications. For example, a connection or an edge can exist between nodes such as “fever” and “vomiting” since the two symptoms happen together in the common flu, meningitis, gastroenteritis, and other underlying infectious diseases while “hair loss” and a “fracture” probably are unrelated and cannot be connected by an edge. Bayesian networks are examples of directed graphical models where the edges have direction and (directed) connections between nodes have cause-and-effect implications. For day-to-day applications, we will drop the requirement that edges be directed and will depart from classical BN theory and work with undirected graphs. Undirected graphs are also called Markov random fields or Markov networks. We will use this structure to enhance data visualization and formulate problems in graphical form to search for solutions [1]. (For the mathematically pure, inference need not be Bayesian in Bayesian networks; frequently these are maximum likelihood-based inferences.) The advantages with this architecture are:
1.
It provides a simple, intuitive, visual understanding of key aspects of a problem.
2.
Helps direct searching large databases like Pubmed for co-occurrences and generating candidates for underlying hypotheses.
3.
Helps evaluate multiple diagnoses in parallel with different likelihoods assigned to different hypothesis.
4.
Can be scaled easily when new observations or symptoms appear.
5.
Can help direct search for new nodes to generate disease patterns.
Once a problem is expressed in the form of nodes, the idea is to construct edges which reflect a relationship between them under a specific hypothesis. In a sense, we are trying to construct a disease “trail” and see how far we can go and connect the nodes with a particular hypothesis or diagnosis in mind. In graph theory a “Trail” is a sequence of edges between vertices which are distinct. We use the term more loosely to mean the sequence of nodes which can be connected together by edges under a particular hypothesis. Based on the principle of Occam’s razor, the better hypothesis is one which can construct a better joint conditional probabilistic relationship between nodes and incorporate more of them under a single diagnosis [1]. As a toy example, a patient comes in with fever, headache. He also reports feeling confused, not remembering where he was when he woke and experiencing neck pain which is worse when looking down. Based on this description, the nodes are the constellation of “fever”, “headache”, “neck stiffness”, “confusion” and the investigator is evaluating whether the underlying condition is Flu or meningitis (Fig. 5.2).

Fig. 5.2
Data visualization. Creating important decision making nodes
Step 1: Problem formulation in graphical form.
Step 2:
(a)
Evaluate the hypothesis of meningitis: Starting with chief symptoms fever, see if meningitis can cause fever and confusion and connect the two nodes. More rigorously, for the mathematically inclined what is the joint conditional probability of fever and confusion occurring if the underlying condition is meningitis? This is expressed as P (Fever, Confusion ∣ Meningitis)? Fairly high, therefore a strong edge can be connected between the two which incorporates our strong belief that the two can happen together if the underlying disease is meningitis. Consider the next node “Headache”; can meningitis connect the pair {fever, confusion} with “headache”? Definitely it can connect the two. Finally can meningitis connect {Fever, confusion, headache} with “neck stiffness”? Definitely. Meningitis can connect all the nodes quite well under our beliefs and we represent this using thicker arrows.
(b)
Evaluate hypothesis of Flu: Going through the above reasoning, Flu can connect Fever, Headache quite well as everyone who has suffered it knows. However connecting the pair of {fever, headache} with confusion? May be. We are not dismissing it so we will connect them with a thinner edge. Can flu connect {Fever, confusion, headache} with “neck stiffness”? Neck soreness as part of body ache can happen, but neck stiffness is unlikely, unless the flu causes viral meningitis/encephalitis in rare instances. Therefore a thinner arrow is used to link such a weak joint probability between them (Fig. 5.3).
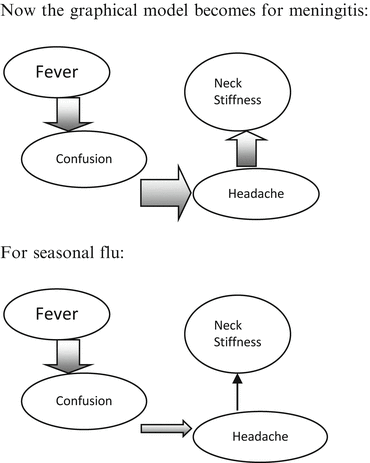
Fig. 5.3
Using graphical methods to construct competing hypothesis for the toy example of a patient presenting with fever, headache, confusion, and neck stiffness
Now the graphical model becomes for meningitis:
Applications of this technique for a few real case examples will be presented. Examples selected are ones where formal application of this structure helped make rare and obscure diagnosis which were elusive for many years and saved costs and directed appropriate treatment. The historical narrative from patient records is presented to demonstrate the great degree of initial filtering required for representing the problem in canonical form for application of these techniques. Case Example 1 is presented with almost all details included from patient records to show the degree of data distillation that is required to perform decision making with medical data. The remaining case examples are edited considerably.
Case Example 1
“BH is a pleasant 65-year-old diabetic female who presents to clinic with her husband for further workup of her sensory ataxia. She has 3 years of progressive sensory ataxia and 6 years of peripheral neuropathy.
She has been having 1–2 falls each week. Her husband states that there is significant staggering when she walks. She relies on a cane and her husband’s help to walk now. The most recent episode was a fall a few days ago. She fell backwards and hit her head without dizziness or loss of consciousness. Balance is worse after sitting for a long time. Patient also complains of fatigue that has been worsening over the past year. She has not broken any bones. She endorses difficulty with memory, remembering names of people and following instructions. She did not notice any changes in her speech or swallowing difficulties. She spends most of the day lying in bed and has experienced some shoulder/neck pain on the left side that is being treated by her primary care doctor. The following tests have been done:”
EMG/NCV: (uncertain date, 2010 or prior) legs showed severe sensory/motor polyneuropathy (diffuse nerve damage). Arms showed bilateral carpal tunnel, left worse than right.
Imaging: 4/27/10 noncontrast MRI brain (per report): no cerebellar/pontine atrophy, no mass/structural lesion, scattered periventricular white matter disease.
7/7/10 carotid duplex: 60–80 % stenosis (narrowing) of proximal left internal carotid artery, 40 % stenosis of proximal right internal carotid artery.
8/4/10 carotid/VA duplex: vertebral artery patent with anterograde flow, left carotid artery shows “a small fibrocalcific plaque at the bifurcation which extends into the origin of the internal carotid artery producing a stenosis (narrowing) in the upper category of 40–59 %.”
Serum: Borderline abnormal TSH (thyroid tests); Normal B12/folate, B1, Vitamin E, Normal electrolytes, liver function, blood counts. Anti Nuclear Antibody normal. Normal serum protein electrophoresis and negative cryoglobulins. Negative anti-Hu, anti-Yo antibodies. Tests for diabetes show well-controlled sugars.
8/17/11 Lumbar puncture—Cerebrospinal Fluid is within normal limits. No abnormalities found.
Medications
1.
SYNTHROID 112 MCG TABS (LEVOTHYROXINE SODIUM)—daily
2.
FUROSEMIDE 40 MG TABS (FUROSEMIDE)—twice daily
3.
TRAZODONE HCL 100 MG TABS (TRAZODONE HCL)—at bedtime
4.
LANTUS INSULIN 18 UNITS AT BEDTIME ()
5.
PROTONIX 40 MG TBEC (PANTOPRAZOLE SODIUM)—daily
6.
DEPAKOTE 250 MG TBEC (DIVALPROEX SODIUM)—one pill three times a day
7.
PROZAC 20 MG CAPS (FLUOXETINE HCL)—three pills daily
8.
LORTAB 5 5–500 MG TABS (HYDROCODONE-ACETAMINOPHEN)—one pill every 6 h as needed
9.
LISINOPRIL TABS (LISINOPRIL TABS)
10.
NORTRIPYTLINE HCL CAPS (NORTRIPTYLINE HCL CAPS)
11.
SIMVASTATIN TABS (SIMVASTATIN TABS)—one tab qD
12.
NORFLEX SOLN (ORPHENADRINE CITRATE SOLN)—100 mg one tablet two times a day
13.
VOLTAREN 1 % GEL (DICLOFENAC SODIUM)
Allergies
1.




NSAIDS—hives, itch
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








