Mechanisms of Injury in the Cervical Spine: Basic Concepts, Biomechanical Modeling, Experimental Evidence, and Clinical Applications
Mark S. Eskander
Jason C. Eck
A thorough understanding of the cervical spine and its mechanisms of injury (MOI) is necessary for evaluation, treatment, and prevention of injury. Knowing the MOI alerts clinicians to suspect specific injury patterns. This knowledge enables physicians to direct the history and physical examination toward specific signs and symptoms. Imaging studies that are more likely to yield useful information will be obtained, and unnecessary studies can be omitted with greater confidence. Clinicians who know which anatomic structures are injured and the extent to which they are compromised are better able to treat the injuries and, in many cases, to prevent further injury.
Often, knowledge of the MOI will aid considerably in the analysis and solution. For example, the realization that rear-end vehicle collisions caused hyperextension injuries of the cervical spine led to the development and widespread use of car seat headrests (1). In 1975, the realization that using the head as a battering ram (spearing) in tackle football could result in cervical quadriplegia led to rules forbidding this type of tackling. Subsequent to implementation of such rules, the prevalence of cervical quadriplegia has dramatically decreased (2,3). A reevaluation of the current diagnostic criteria for shaken baby syndrome is warranted after a biomechanical analysis of previous studies regarding the injury mechanism (4,5). Another example is illustrated in a study by Hoek Van Dijke et al. (5). In response to the observation that pilots of highperformance aircraft frequently sustained cervical spine injuries due to their exposure to high gravitational forces (6), investigators measured accelerations about the head of an F-16 fighter pilot during simulated air combat maneuvers. With the aid of a spine model, the investigators calculated the forces on the lower cervical spine and noted that the forces were of the same order of magnitude as failure loads of cervical vertebrae and estimations of maximum cervical spine muscle forces. Forces on the neck could be substantially reduced by decreasing the mass of the pilot’s helmet or shifting the center of mass of the helmet dorsally, thus potentially reducing the risk of cervical spine injury. In litigation cases, an analysis of the MOI can help determine responsibility for a given cervical spine injury. Evaluating the MOI thus becomes an important component of medicolegal analyses.
KEY BIOMECHANICAL CONCEPTS
One may observe distinctly different cervical spine injury patterns, such as dens fractures or bilateral facet dislocations, in different persons who have been involved in apparently similar accidents, such as falling from a ladder. Closer examination, however, discloses that what at first appeared to have been similar accidents actually represented several very different circumstances. From a biomechanical perspective, the conditions in which the accident occurs, or the MOI, cannot be adequately described by a simple explanation of the event that led to the injury. A statement such as “The patient fell from a ladder” does not specify the height from which the subject fell, the subject’s weight, the point that first contacted the ground, the position of the subject’s head and neck at the time of contact, or the characteristics of the surface onto which the patient fell. When one realizes that each of these conditions can differ greatly and that each specific injury pattern is due to a specific set of conditions, one can begin to appreciate the complexities of describing injury mechanisms. Only after all conditions have been considered can one begin to understand the true MOI.
TABLE 5.1 Variability of Load at Failure of Human Cadaveric Cervical Spines | |||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||||||
This chapter focuses on seven basic biomechanical concepts that the authors believe characterize the conditions that result in any specific injury of the cervical spine:
Magnitude of the force
Rate of load application
Displacement
Direction of the force relative to the subject or spine
Point of load application
Preposition of the head and functional spinal units (FSUs)
Anatomic, material, and structural characteristics of the spine at the site of injury
These concepts address the conditions that should be noted in all studies of the production of cervical spine injuries. Differences in these conditions may account for some of the large variations in loads to failure within and between studies on cadaveric cervical spines (Table 5.1).
MAGNITUDE OF THE FORCE
Force is defined as any action that tends to change the state of rest or motion of a body to which it is applied. Force is a vector quantity that has magnitude and direction. The unit of measure for the magnitude of force is newtons (N).
Instantaneous failure is failure that results from a single (ultimate) load cycle. Fatigue failure is failure that results from the growth of cracks in structures subjected to repetitive load cycles. The lowest load that will cause fatigue failure within a reasonable time is the fatigue, or endurance, limit. The process of fatigue is documented by fatigue curves. The load is plotted on the ordinate, and the number of load cycles to failure, in a logarithmic scale, is plotted on the abscissa. Generally, a straight line connects the ultimate load and the endurance limit points. (When the load on the ordinate is replaced by stress, then the fatigue curve is called stress—number of cycles to failure or simply an S-N curve.) More simply, cumulative loading can result in fatigue failure, and the greater the load in excess of the endurance limit, the fewer number of cycles are required to reach failure.
For steel, cyclic loads of magnitudes as low as 20% of the ultimate failure load will cause fatigue failure. Similar failure can occur in cortical bone at 35% of the failure load. However, in vivo, the fatigue limit is probably greater than 35% because reparative biologic processes may compensate for the propagation of fatigue cracks.
RATE OF LOAD APPLICATION
Because biologic tissues are sensitive to the rate of loading, changing the load rate may alter the pattern and severity of injury. Consideration of the concept of viscoelasticity is useful.
Viscoelasticity is defined as the time-dependent property of a material to show sensitivity to rate of loading or deformation. Creep and relaxation are two characteristics of viscoelastic materials that can be quantitatively documented. During creep tests, the load is suddenly applied and is kept constant; the resulting displacement is recorded as a function of time. In relaxation tests, a deformation is produced and held constant while the resulting decrease in load is recorded as a function of time.
Bone, ligaments, tendons, and passive muscles demonstrate viscoelastic behavior. Because of this viscoelastic behavior, their stress-strain curves are dependent on the rate of loading. In general, the greater the rate of loading, the steeper the resulting curves become; however, the rate of change of the stress-strain curve slope as a function of increasing rate of loading is not identical for bone, ligaments, tendons, and passive muscles.
Increasing the tensile loading rate of an anterior cruciate bone-ligament-bone preparation increases the probability that ligament failure will occur before bone failure (7). In the cervical spine, increasing the axial compression loading rate increases the probability of single-level vertebral body fractures, whereas quasistatically loaded cervical spines are more likely to sustain multilevel bony and ligamentous injuries.
Increasing the loading rate also increases the energy absorption to failure (8) and the energy dissipated in the surrounding tissues. Yoganandan et al. (9) characterized the uniaxial dynamic tensile response of human cervical anterior longitudinal ligaments and ligamentum flavum for loading rates at 9 to 2,500 mm/s. They reported that the ultimate tensile failure load and energy-absorbing capacity at failure increased nonlinearly with the logarithm of the loading rate (10). Other investigators have found similar responses in compact bone and ligaments (7,10).
In accidents, energy-absorbing materials positioned at the point of head impact can increase the time over which the spine is loaded, effectively reducing the rate of loading. This reduces the peak impact force but does not necessarily reduce the total energy transferred to the neck or to a cadaver model (11). In some cases, deflection of the head and neck can result in forces being dissipated to
the shoulders or chest. Energy-absorbing materials, however, have the propensity to pocket the skull upon impact, preventing it from being deflected out of the path of the load. If the final position of the head or FSU is limited or constrained, tested human cadaveric cervical spines have shown increased energy at failure and increased injury in comparison with unconstrained specimens (8).
the shoulders or chest. Energy-absorbing materials, however, have the propensity to pocket the skull upon impact, preventing it from being deflected out of the path of the load. If the final position of the head or FSU is limited or constrained, tested human cadaveric cervical spines have shown increased energy at failure and increased injury in comparison with unconstrained specimens (8).
These studies indicate that padded surfaces that protect the skull at impact may not reduce and may even increase the risk and extent of cervical spine injury. However, one must recognize the important and proven efficacy of padded surfaces in the prevention of head and facial injuries and the reduction of contusions and fractures in other areas of the body. The authors are not suggesting that padded protective surfaces be eliminated but believe that the possible increased risk of injury to the cervical spine with padded protective surfaces must be weighed against the notably decreased risk of injury to other areas of the body.
DISPLACEMENT
Work is the product of force times distance. Energy is the work done. The unit of work or energy is the newton-meter (N-m) or joule (J). When a load deforms the body, the corresponding energy is termed strain energy; when a load displaces the body, the corresponding energy is termed potential energy. If a load imparts motion to the body, the energy is termed kinetic energy.
For a given load, greater displacements result in more severe cervical spine injury (12,13). The concept of limiting extremes of motion to prevent injury led to the provision of headrests on car seats and of shoulder neck rolls for football linemen. Seatbelt restraints have been shown to reduce the prevalence of severe cervical spine injuries significantly (14).
The flexibility of the spine varies at different load magnitudes. Studies of the lumbar spine (15, 16 and 17) have shown that the spine easily deforms at smaller loads. As the load increases, the resistance to deformation increases at an increasing rate. A similar response is assumed in the cervical spine.
The Neutral, Elastic, and Plastic Zones
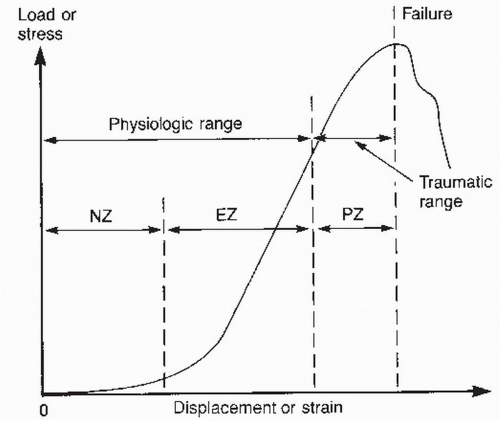
The load-displacement curve for a particular FSU has three regions: the neutral zone (NZ), the elastic zone (EZ), and the plastic zone (PZ). (For zone definitions, see Chapter 4.) The sum of the NZ and EZ constitutes the physiologic range of motion (ROM), whereas the PZ is the region of trauma.
Oxland and Panjabi (18, 19 and 20) hypothesize that the NZ correlates with other parameters indicative of spinal instability and is probably more sensitive than corresponding changes in ROM (Fig. 5.1). The NZ increases with injury to the spinal column. They further hypothesized that the neuromuscular system can compensate for the increased NZ by increased muscle activity, which may, however, increase the muscle fatigue and risk for further injury. If the neuromuscular system is not able to fully compensate, due to either extensive injury to the spinal column or muscle fatigue, the resultant instability may lead to neurologic injury, deformity, or pain.
Instantaneous Axis of Rotation
Displacement occurs relative to a fixed axis in space. When a rigid body moves in a plane, at every instant there is a point in the body or in some hypothetical extension of it that does not move. An axis perpendicular to the plane of motion and passing through that point is the instantaneous axis (center) of rotation (IAR) for that motion at that instant. Although the spine as a whole is not a rigid body, each vertebra (and the skull) is a relative rigid body, and thus, the movement of one vertebra (or the skull) relative to an axis creates an IAR. Differences in the IAR cause differences in injury patterns.
Two separate studies utilizing similar mechanical testing apparatuses with different IARs loaded human cervical spinal segments in flexion and axial compression. McLain et al. (21) used a center of rotation ventral to the vertebral bodies and a loading rate of 50 mm/min (0.85 mm/s), to produce a 5 N-m flexion moment. They noted injuries to all dorsal soft tissue articulations prior to disruption of the annulus and no fractures. In contrast, Crowell et al. (22) used an axis of rotation at the center of the middle vertebrae and a loading rate of 3 to 5 mm/s and failed the specimens at a 7 ± 5 N-m flexion moment. They produced dorsal ligament damage in only two of five specimens, but all five sustained intervertebral disk injuries. There was one wedge fracture of a vertebral body.
DIRECTION OF LOAD RELATIVE TO THE SUBJECT OR SPINE
The direction of load is an important determinant of MOI. It can be evaluated either in a uniplanar analysis or more extensively in three dimensions.
Uniplanar Analysis
Most classification systems for cervical spine injuries describe forces occurring in the sagittal or frontal plane. Clearly, uniplanar systems involving single forces or moments (e.g., “flexion injuries”) do not fully describe the multitude of injury patterns that occur in the cervical spine. However, as a first approximation, the uniplanar sagittal plane analysis is useful. Analysis in the sagittal plane demonstrates a spectrum of injury patterns for which a variety of combinations of compression forces and bending moments describe a “family” of injuries (Fig. 5.2).
Uniplanar analysis limits one to evaluations of load and displacement in three degrees of freedom (DOF). For example, in the sagittal plane (the yz-plane in Fig. 5.2), analysis is limited to forces and translations along the z-axis (first of three degrees) and y-axis (second of three degrees) and moments and rotations about the x-axis (third of three degrees).
Analysis in Three Dimensions
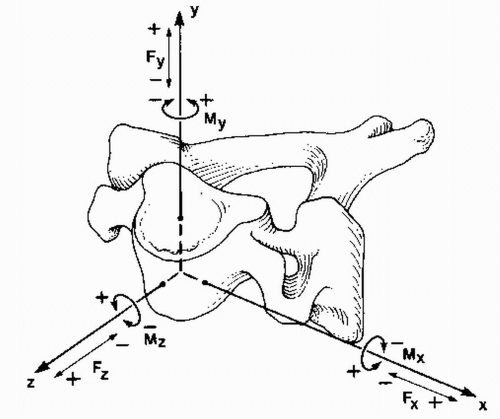
A multiplanar coordinate system (Fig. 5.3) allows one to evaluate the possible loads (forces and moments) and corresponding six possible displacements (translations and rotations) along and about three orthogonal axes. This six-DOF analysis allows a more complete description and evaluation of the biomechanical environment.
Coupling
Coupling is a phenomenon in which there is a consistent association of translation or rotation about or along one axis with a translation or rotation about or along another axis. It has been described in both the upper and lower cervical spine (see Fig. 4.9). Data for the upper cervical spine suggest that three-dimensional (3-D) relative motions are affected by prepositioning in full flexion, neutral, or full extension (23). Attempts have been made to quantify this process through mathematical relationships describing the coupled motion that occurs with axial rotation and lateral bending of the head-neck complex. With the aid of a 3-D motion analyzer, the coupling effect was traced throughout the full range of unrestricted head-neck motion. Values for primary and coupled ROMs were obtained,
suggesting no significant difference between male and female primary ROMs but a small disparity between male and female coupled ROMs (24). The role of age and its influence on primary and coupled movements have been examined. With increasing age, primary movement size decreases in all cardinal planes. Age most strongly affects the coupled movements of primary rotation and lateral flexion. Gender and body mass index demonstrate only a marginal influence (25).
suggesting no significant difference between male and female primary ROMs but a small disparity between male and female coupled ROMs (24). The role of age and its influence on primary and coupled movements have been examined. With increasing age, primary movement size decreases in all cardinal planes. Age most strongly affects the coupled movements of primary rotation and lateral flexion. Gender and body mass index demonstrate only a marginal influence (25).
Major Injuring Vector
Although many injuries are viewed in the sagittal plane (such as on lateral radiographs), a spectrum of injuries may be observed in any of the three traditional planes: sagittal (zy), frontal (xy), and horizontal (xz) (26). Spinal injury analysis may involve major forces that are not predominantly in the sagittal (yz), frontal (xy), or horizontal (xz) planes (Fig. 5.3).
Any given injury may result from a complex set of external forces and moments applied to the body. Because the site of injury is often different from the points of external force applications, these external forces generate additional moments at the site of injury. The major injuring vector (MIV) is a representation of the total (external plus additional) moments and forces at the injury site. The concept of describing the forces and moments experienced at the particular level of injury as opposed to describing these forces and moments in relation to the point of impact of an externally applied load can add a degree of precision to the description of the forces causing a specific injury. Studies of whole spines and cadavers indicate that external mechanical conditions (forces and moments applied to the head) do not always reflect the segmental conditions and patterns of injury at the level of the individual cervical vertebrae (11, 12 and 13,27,28). An axial force applied to a specimen including the occiput to T1 may produce a component of sagittal plane flexion moment at the occipitoatlantal joint while simultaneously producing a component of sagittal plane extension moment in the lower cervical segments. In this case, the MIV can more precisely describe the complex forces and moments that occur at each site of injury.
Consideration of the potential difference between the externally applied force and moment and the MIV is necessary when one reviews biomechanical studies that reproduce injury patterns by loading isolated segments containing only one or several FSUs as compared with studies in which entire head-to-T1 specimens are used.
POINT OF LOAD APPLICATION
Human cadaveric specimens axially loaded dorsal to the vertex of the skull fail in extension, and those loaded ventral to the vertex fail in flexion (29). Small (1 cm) variations in anterior-to-posterior distance from neutral in the point of axial load application produce great variations in the resultant fractures (30), as was demonstrated in porcine models (31, 32 and 33) by dropping a 14.5-kg mass from a height of 1.1 m onto a cylinder placed over a vertebral body. When the cylinder was centered over the geometric center of the vertebral body, the lowest degree of injury was produced—and in no consistent anatomic pattern. Positioning the cylinder 1 cm ventral to the geometric center of the vertebral body produced both the most severe damage to the dorsal elements and flexion instability. A cylinder positioned 1 cm dorsal to the geometric center produced both the most severe damage to the ventral elements and extension instability. Nightingale and associates sought to understand the MOI in a study where cadavers were dropped in an inverted posture with the head and neck in an anatomically neutral position. Observable head motion did not correspond to the mechanism of the injury to the cervical spine. However, the classification of the mechanism of the injuries was descriptive of the local deformations of the cervical spine at the time of the injury. Thus, these classifications can be useful for describing the local MOI. Buckling of the cervical spine involving extension between the third and sixth cervical vertebrae and flexion between the seventh and eighth cervical vertebrae was noted. Other, more complex, buckling deformations were also observed, suggesting that the deformations that occur during impact are so complex that they can beget several different MOI (34).
Nonaxial net forces may result in deflection of the head and neck (8). If this occurs, a sizable portion of the load may be borne by the shoulders instead of the head and neck. (See the discussion of energy-absorbing materials in the section “Rate of Load Application” earlier in this chapter.)
PREPOSITION OF HEAD AND FUNCTIONAL SPINAL UNITS
Human cadaveric and calf spine studies demonstrated that the initial head-neck-thorax position and loading conditions dictate the cervical spine response to impact (11,35, 36, 37 and 38). The response in the sagittal (yz) plane includes flexion, buckling, and extension.
A subject buckles under axial centrally applied load if there is sudden “give” or deformation of the structure. This occurs with an axial force when the cervical spine is straight and colinear; it is to be distinguished from bending, which may be caused by an axial load applied to a spine with notable lordosis or kyphosis. In the case of bending, the structure will begin to bend immediately after application of the force. There is no sudden buckling or giving way (Fig. 5.4). Differences in point of load application and direction of the load relative to the spine or subject may also affect the spine’s response of beading or buckling.
In human cadaveric testing, prepositioning of the head in a slightly flexed position to eliminate the normal cervical lordosis (thus straightening the spine) results in the least amount of axial deformation under a given axial compression load (Fig. 5.5). This theoretically lessens the ability of the surrounding muscles and ligaments to dissipate the applied energy gradually, as might occur in the case of bending. With a straightened spine, large amounts of energy are absorbed by the spinal column until it buckles, at which point the stored energy is rapidly dissipated to the surrounding soft tissues.
Hamalainen and Vanharanta (39) demonstrated significantly higher cervical erector spinae muscle electromyogram maximum supportable loads in simulated pilot ejections to be 30, 24, and 15 G for the neutral, flexed, and
extended postures, respectively. These studies support the assertion that jet fighter pilots who maintain their heads in neutral position can expect their necks to absorb more energy before failure; that is, if they maintain their necks in a neutral position, injury is less likely to occur.
extended postures, respectively. These studies support the assertion that jet fighter pilots who maintain their heads in neutral position can expect their necks to absorb more energy before failure; that is, if they maintain their necks in a neutral position, injury is less likely to occur.
Cadaver specimens prepositioned in flexion (kyphosis) or extension (lordosis) and then axially loaded failed in flexion or extensions at much lower loads than did the neutral-positioned specimens (29,40). These and other cadaveric studies as well as theoretical mathematical models (41, 42 and 43) suggest that the straightened (rather than lordotic or kyphotic) cervical spine will sustain and withstand the highest externally applied axial load.
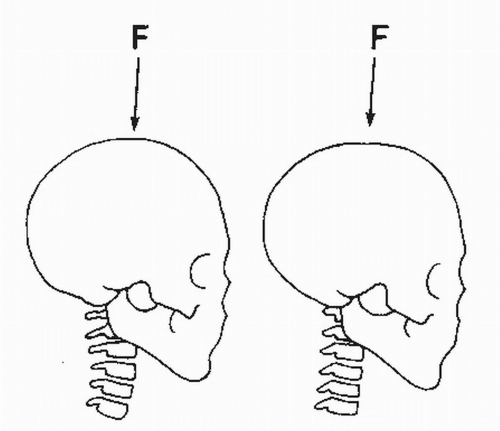
Clinically, the importance of the preposition of the head and FSU is exemplified in diving injuries. Recreational diving accounts for 54% to 66% of all sports-related cervical spine injuries (8). Most injuries occur during diving headfirst into shallow water with a flexed neck. This results in a “snap-roll” motion on impact with the ground or pool bottom and injuries that include compression and burst fractures and facet dislocations. In contrast, shallow diving with the neck extended results in facial injuries. There is a relatively low prevalence of serious neck injuries reported with facial-impact diving injuries.
ANATOMIC, STRUCTURAL, AND MATERIAL CHARACTERISTICS
The material and structural properties of objects markedly affect the failure patterns that occur as a result of the various loads applied to them. Considerable difference exists in the individual anatomic variability among subjects. Within the same subject, changes occur in the material and structural properties due to conditions associated with disease and with the normal aging process. Harty et al. performed an anthropometrical analysis of cervical spines. Measurements of head circumference, neck circumference, chest circumference, and neck length were analyzed. The results suggested that a proportionately larger chest may provide protection in cervical spine fractures (44).
Size and Shape
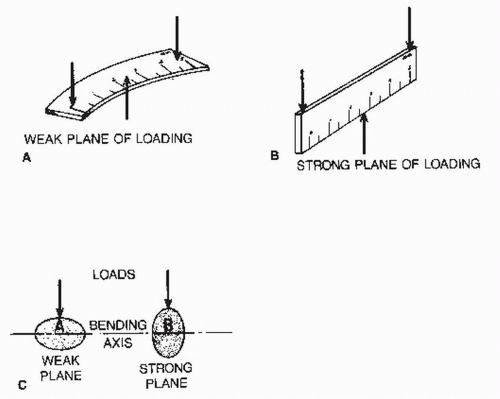
The sectional or area moment of inertia is a measure of the distribution of a material in a certain manner about
its centroid (the point on which the total area may be centered) (Fig. 5.6). This distribution determines the strength in bending.
its centroid (the point on which the total area may be centered) (Fig. 5.6). This distribution determines the strength in bending.
Objects similar in size and material properties may have large differences in bending strength based on differences in their sectional moment of inertia. The relevance of this concept is demonstrated in interpretations of studies in which the structural properties of surgical constructs or injury patterns are described using animal models with vertebral bodies similar in size but differing in shape from those of humans. Despite similarities in size, differences in shape may affect bending stiffness and patterns of failure, rendering comparisons between certain animal and human models of trauma inaccurate.
Age and Osteoporosis
There is a linear decrease in bone mineral content with increasing age (45). The rate of decrease is not different between males and females, but the bone mineral content at any age is less in females than in males of the same age.
Lotz et al. (46) demonstrated that the compressive strength of trabecular bone is proportional to the square of its apparent density. Bell et al. (47) reported that a small loss of osseous tissue produces considerable loss in vertebral bone strength; that is, a 25% decrease in the osseous tissue results in a more than 50% decrease in the strength of the vertebra. This emphasizes the importance of accurate measurement of the bone mineral density of specimens, since a 25% decrease in osseous tissue is not apparent in plain radiographs and yet results in a more than 50% decrease in strength. Stulík et al. (48) reported that even low-energy trauma can have devastating effects to the upper cervical spine involving neurologic deficits typically manifesting as a central cord syndrome. In the elderly population, extra precautions must be taken with seemingly minor events. The implications of the importance of maintaining bone mass to prevent osteoporotic fractures, though uncommon in the cervical spine, are clear.
Age and Ligament Strength
Considerable work has been done to characterize the change in soft tissue related to aging (49). With aging, degenerative changes in soft tissues can weaken them, resulting in injuries from very low-energy trauma. These injuries have been described in the shoulder, knee, and foot (40,49, 50 and 51). In most studies evaluating age-related changes in ligament strength, the tensile properties of the ligaments of the knee have been examined. Human cadaveric studies of the anterior cruciate ligament reflect decreasing tensile stiffness and ultimate load to failure with increasing age (52,53).
Changes in the ligamentum flavum at the cellular level include decreased cellularity and increased fragmentation of elastic fibers with substitution fibrosus (54). Biomechanically, aging of the ligamentum flavum causes decreased modulus of elasticity and decreased ultimate strength. Little work has been done to evaluate changes in the physical and material properties of other spinal ligaments or facet capsules with age (55).
Studies evaluating age-related changes of the intervertebral disk have concentrated on the lumbar segments. There is a decrease in proteoglycans and water concentration and an increase in noncollagenous protein concentration (49). Structurally, the annulus becomes fissured. These changes alter the load-sharing and dampening properties of the intervertebral disk. In the lumbar spine, this results in less central end plate fracturing (Schmorl’s nodes) and more vertebral body compression fractures with advancing age. Schmorl’s nodes and atraumatic compression fractures are rarely noted in the cervical spine; presumably, the relatively lower magnitude of loading accounts for the much lower occurrence of these types of fractures.
Fused Segments (Structural Changes)
Multiple adjacent fused cervical spine segments create a long, stiff lever arm. A condition of increased stress concentration occurs. Stress concentration is a sudden change in material or structure, or both, that creates a localized stress peak that cannot be predicted by a simple theory regarding strength of material. This increased stress concentration is due to an abrupt change in modulus, or stiffness, along the spine adjacent to fused segments. When areas of increased stress concentration exist in the cervical spine, major injuries can occur after minor cervical spine trauma. Fusion of multiple cervical spine FSUs can occur congenitally in Klippel-Feil syndrome, developmentally in degenerative ankylosis and ankylosing spondylitis or iatrogenically after surgical arthrodesis.
Spinal segments adjacent to fused segments may become unstable in patients with Klippel-Feil syndrome. A case of a patient with congenital fusion of several vertebrae who sustained minor trauma (falling back against a car) that resulted in quadriplegia has been reported (56).
In ankylosing spondylitis, the increased stress concentration occurs in the lower cervical spine, where most
fractures occur. Mechanisms of hyperextension (57,58) and flexion (59) have been proposed. Major spinal cord compression may occur from bony displacement or epidural hematoma. The difficulty of treating cervical spine fractures involving ankylosing spondylitis relates to the propensity for displacement. This problem is most likely due to the long segment or segments of spine adjacent to the fracture. Despite the loss of elasticity at ankylosed segments, three cases of spinal cord compression from herniated nucleus pulposus have been reported (59).
fractures occur. Mechanisms of hyperextension (57,58) and flexion (59) have been proposed. Major spinal cord compression may occur from bony displacement or epidural hematoma. The difficulty of treating cervical spine fractures involving ankylosing spondylitis relates to the propensity for displacement. This problem is most likely due to the long segment or segments of spine adjacent to the fracture. Despite the loss of elasticity at ankylosed segments, three cases of spinal cord compression from herniated nucleus pulposus have been reported (59).
In 12 of 15 patients whose diagnosis included surgical and congenital fusions of the cervical spine as well as degenerative ankylosis, MacMillan and Stauffer (60) reported posttraumatic instability closely associated with the location of the fusion mass.
SUMMARY OF KEY BIOMECHANICAL CONCEPTS
The specific injury sustained as a result of a load is dependent on the characteristics of that load, the response of the spine or FSU, and the individual anatomic, structural, and material variations existing in each subject. The magnitude of the injuring force and the number of times it is applied determine whether the subject fails instantaneously or in fatigue failure. The rate of load application partly determines the amount of energy absorption to failure and whether the failure occurs primarily through bony or soft tissue elements. The direction of load relative to the spine, the position of the head, and the point of load application determine the response of the spine to axial load. Based on the particular combination of the preceding conditions, the spine will buckle, flex, or extend. Each of the preceding responses will produce a different complex of injuries. The threshold for failure in the cervical spine may be raised or lowered by many variables, including normal anatomic variation and certain diseases that affect material or structural properties or both (61, 62 and 63).
The seven concepts just discussed may be considered and analyzed under both experimental and clinical conditions. In studies of cervical spine injury mechanisms, it is worthwhile to consider these concepts and to address them in the experimental design. In the clinical setting, however, the information required for full assessment of these concepts is rarely available. Patients present to the emergency room either comatose, intoxicated, or unable to recall the events of the accident. In such cases, a thorough physical examination to detect specific areas of tenderness or contusions and a complete radiographic evaluation can help one deduce the MOI. For an in-depth analysis of the MOI of a particular injury, it is useful to consider each of the seven concepts and make a determination regarding its applicability or role.
BIOMECHANICAL MODELING
A biomechanical model is a simulator in a laboratory of some aspects of human reality. Several types of models exist, with various advantages and disadvantages. The most common types of biomechanical models are in vivo animal, cadaveric, synthetic, and computer models.
The cadaver model may be a whole cadaver, a multiple-vertebrae segment, or an FSU. For biomechanical studies of injuries, all three types of cadaver models have been used. Advantages of these models include faithful reproduction of the anatomy and physical properties of the osteoligamentous spine. Disadvantages include variability from specimen to specimen, lack of availability, and high cost. One can argue that the variability is an asset because it truly represents the reality in the human population. The variability makes it possible to study the effects of age and disease on the physical characteristics of the spine. The variability observed clinically in injuries is thus automatically simulated in experimental trauma using cadaveric models.
Animal cadavers have been used in spine injury research. The obvious disadvantage is the dissimilar anatomy and physical properties. However, availability and greater uniformity in size, internal architecture, and physical characteristics have made them useful for certain types of studies, such as cervical spine trauma (32).
In vivo animal models have been used for spinal injury research, mostly for the study of the effects of healing in ligament and disk injuries and spinal arthrodesis (64—68). Because the anatomy and physical characteristics of animals differ greatly from those of humans, the usefulness of such models in advancing our understanding of injury mechanisms is limited.
Synthetic models of the spine simulate actual spine behavior by incorporating the physical characteristics of the vertebrae, anatomic geometry, and physical characteristics of the soft tissues connecting the vertebrae. Synthetic models, such as Hybrid III car crash dummies, have vertebrae consisting of a hard material such as plastic or steel; the soft tissues are simulated by synthetic rubber of appropriate hardness. The advantages of the synthetic models are that they are highly reproducible and easily obtained. Because they can be used repeatedly without deterioration in their behavior, they are economical. A disadvantage of the present designs is their inability to validly simulate actual spine behavior. For example, the biomechanical response (i.e., the load-displacement curve) of the Hybrid III model neck has been documented to be three to five times stiffer than that of the cadaveric cervical spine (69). Another disadvantage of the synthetic models is their lack of anatomic detail. One cannot identify a specific anatomic element, such as the capsular ligament or facetjoint. This is necessary if one is interested in the effects of injuries on specific anatomic elements. Another limitation of most of these models is their lack of simulation of the muscular system. To the authors’ knowledge, only one model has incorporated muscles (70,71).
The lack of muscle simulation may not be a major disadvantage in the study of injury mechanisms because the reaction time necessary for muscle force generation is too long to be effective in most spinal trauma circumstances; that is, the muscles are too slow to react in a traumatic situation to play a major role in actual injury. Muscle force development time is slow (100 to 200 ms) compared with the rise time (5 to 10 ms) of the loads causing the injury (72,73). Whole cadaveric models incorporate passive muscle properties. Some investigators have included muscle function simulation by applying forces to the cadaveric specimens (74,75).
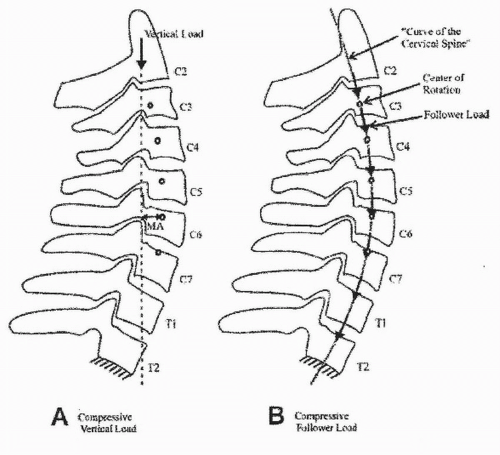
Some authors, unsatisfied with the explanation for the discrepancies between estimated in vivo and ex vivo load carrying capacities of the human cervical spine, designed an experiment to resolve this issue. The authors describe how a cervical spine can be lordotic but yet withstand large compressive loads estimated in vivo without damage or instability (76). They note that the load-carrying capacity of the ligamentous cervical spine sharply increases under a compressive follower load (76). Figure 5.7 illustrates the cervical follower load technique as described by Patwardhan et al.
Computer or mathematical models are sets of equations that incorporate experimentally obtained physical properties of the soft tissues and geometry of the vertebrae (43,77). Mathematical models will be very useful when they can validly incorporate physical characteristics of an osteoligamentous spine and mathematically simulate the muscular forces. Current computer models use finite-element methods, a sophisticated mathematical technique. However, the authors know of no fully validated mathematical models available for the study of injury mechanisms of the cervical spine. Comprehensive validation of these complex mathematical tools is a challenging endeavor.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree