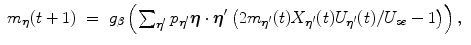(1)
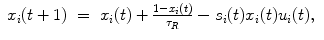
(2)
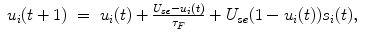
(3)
![$$h_{i}(t) =\sum _{ j\neq i}^{N}J_{ij}[2s_{j}(t)x_{j}(t)u_{j}(t)/U_{se} - 1]$$](/wp-content/uploads/2016/09/A315578_1_En_68_Chapter_IEq1.gif) represents the total input to the ith neuron and
represents the total input to the ith neuron and 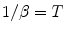 represents the noise intensity. The quantity J ij represents the absolute strength of the connection from the jth to ith neuron; the memory patterns are stored in this connections. U se represents the steady state value of the variable u i (t). The strength of synaptic transmission is given by the product of x j (t) and u j (t); the strength decreases (depression) or increases (facilitation) depending on the parameters τ R , τ F , and U se .
represents the noise intensity. The quantity J ij represents the absolute strength of the connection from the jth to ith neuron; the memory patterns are stored in this connections. U se represents the steady state value of the variable u i (t). The strength of synaptic transmission is given by the product of x j (t) and u j (t); the strength decreases (depression) or increases (facilitation) depending on the parameters τ R , τ F , and U se .The associative memory network is implemented with following absolute strength of synaptic connection 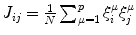 where J ii = 0. The p memory patterns
where J ii = 0. The p memory patterns 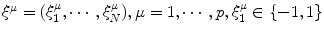 are given by the following correlated patterns. Suppose that a parent memory pattern ξ, which satisfy
are given by the following correlated patterns. Suppose that a parent memory pattern ξ, which satisfy ![$$\mathrm{Prob}[\xi _{i} = \pm 1] = 1/2$$](/wp-content/uploads/2016/09/A315578_1_En_68_Chapter_IEq5.gif) . The memory patterns ξ μ are given by
. The memory patterns ξ μ are given by ![$$\mathrm{Prob}[\xi _{i}^{\mu } = \pm 1] = (1 \pm b\xi _{i})/2$$](/wp-content/uploads/2016/09/A315578_1_En_68_Chapter_IEq6.gif) , where b is the correlation level among memory patterns and takes values in the interval [0, 1].
, where b is the correlation level among memory patterns and takes values in the interval [0, 1].
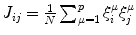 where J ii = 0. The p memory patterns
where J ii = 0. The p memory patterns 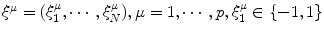 are given by the following correlated patterns. Suppose that a parent memory pattern ξ, which satisfy
are given by the following correlated patterns. Suppose that a parent memory pattern ξ, which satisfy ![$$\mathrm{Prob}[\xi _{i} = \pm 1] = 1/2$$](/wp-content/uploads/2016/09/A315578_1_En_68_Chapter_IEq5.gif) . The memory patterns ξ μ are given by
. The memory patterns ξ μ are given by ![$$\mathrm{Prob}[\xi _{i}^{\mu } = \pm 1] = (1 \pm b\xi _{i})/2$$](/wp-content/uploads/2016/09/A315578_1_En_68_Chapter_IEq6.gif) , where b is the correlation level among memory patterns and takes values in the interval [0, 1].
, where b is the correlation level among memory patterns and takes values in the interval [0, 1].To analyze the macroscopic properties of the associative memory network, we consider the following macroscopic mean field model that captures overall dynamical properties of the network [4].