Modulation of Synchrony in Primates’ Medial Motor Areas

Fig. 1

(a) Experimental setup (b) Task sequence (c) Schematic drawing of medial motor areas (top view)

After each animal became proficient in performing this behavioral task, an acrylic recording chamber and head-fixation bolts were implanted on the animal’s skull. After complete recovery from the surgery, we used glass-insulated Elgiloy microelectrodes to make simultaneous recordings of LFPs for the SMA and pre-SMA in one hemisphere while the subjects performed the task (Fig. 1c). Online data collection was performed using a multichannel acquisition processor. Eye position was monitored using an infrared corneal-reflection-monitoring system at 1 kHz (Millennium G200, Matrox).

As a spectral measure of the correlation of the two signals across frequencies, we calculated the coherence from the cross-spectral density between the two LFPs and normalized it by the power spectral density of each [4] using the LFPs recorded in visually guided trials. Coherence values range from 0 to 1. A value of 0 indicates that the two signals were completely uncorrelated, whereas a value of 1 indicates that the signals were completely correlated at frequency f. We defined the frequency that yielded the greatest coherence in the β band (15–40 Hz) as the frequency of interest (f ₀) for further analysis.

Our main interest was the cue-dependent modulation of inter-area β oscillations during visually guided trials. We thus defined five consecutive analytic periods in a visually guided trial, as shown at the bottom of Fig. 1b: intertrial period (IT), trial-initiation period (INI), instruction-cue period (INST), motor-preparation period (PREP), and motor-execution period (EXE). To extract the instantaneous phase for the frequency f ₀, we applied a wavelet-based approach. The signal of the LFP was convoluted by a complex Gabor’s wavelet w(f ₀, t):

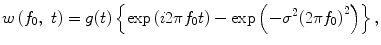
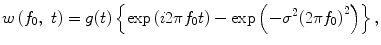
$w\left({f}_0,\ t\right)=g(t)\left\{ \exp \left(i2\pi {f}_0t\right)- \exp \left(-{\sigma}^2{\left(2\pi {f}_0\right)}^2\right)\right\},$

where

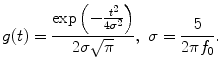
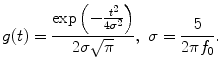
$g(t)=\frac{ \exp \left(-\frac{t^2}{4{\sigma}^2}\right)}{2\sigma \sqrt{\pi }},\ \sigma =\frac{5}{2\pi {f}_0}.$

The instantaneous phase difference between a pair of electrodes Δφ(f ₀, t) was expressed as the relative phase of the signal recorded from the pre-SMA to that from the SMA:

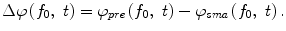
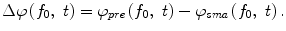
$\Delta \varphi \left({f}_0,\ t\right)={\varphi}_{pre}\left({f}_0,\ t\right)-{\varphi}_{sma}\left({f}_0,\ t\right).$

To determine the strength of inter-hemispheric phase synchronization, we calculated a phase-synchronization index (PSI) for a given 500-ms analytic period in a trial as the mean vector length of the angular dispersions of the phase differences in the analytic period [5]. If the phase difference varies little in the analytic period, the PSI is close to 1; otherwise, it is close to 0. 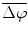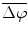To examine how the presentations of the initiation cue and the motor instructional cue influenced the inter-area phase relationship, we computed the mean phase difference $\overline{\Delta \varphi }$ for the IT, INI, and INST periods in each recording session. 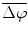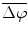$\overline{\Delta \varphi }$ was calculated as the angle of the circular mean of the phase differences observed in the analytic period across trials.

3 Results

We performed a total of 30 paired recordings (15 sessions in each hemisphere) for monkey M and 61 (29 and 32 sessions in the left and right hemisphere, respectively) for monkey N. Coherence analysis revealed that f ₀ = 35 Hz for monkey M, and f ₀ = 22 Hz for monkey N. The dynamics of the inter-area phase difference and the strength of the phase synchronization between areas based on the analysis for the frequency f ₀ are discussed in the next section.

Only gold members can continue reading. Log In or Register to continue