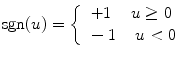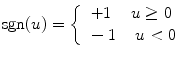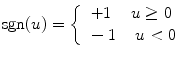Multichannel Communication Using Chaos in a Recurrent Neural Network

$\mathrm{sgn}(u)=\left\{\begin{array}{c}\hfill +1\kern1.25em u\ge 0\hfill \\ {}\hfill -1\kern1.25em u<0\hfill \end{array}\right.$

where x _i(t) = ±1(i =1 ∼ N) is the firing state of a neuron specified by index i at time t, w _ijis connection weight from the neuron x _jto the neuron x _i. w _iiis taken to be 0. r (0 < r < N) is fan-in number for neuron x _i, named connectivity that is the most important system parameter in our work. G _i(r) is a spatial configuration set of connectivity r for neuron x _i,, the number of which are _N-1C_r. Therefore, with full connectivity r = N − 1, determination of w _ijby means of a kind of orthogonalized learning method enables us to embed a group of N dimensional state patterns as cyclic memory attractors. In our works, attractor patterns consists of (K patterns per cycle) × L cycles, and each patterns has N neurons. In this work, we take K = 15, L = 2 (see Fig. 1), or K = 10, L = 3 (see Fig. 4), and N = 400, where the firing states of N = 20 × 20 = 400 neurons are represented by black pixel or white pixel as shown in Fig. 1. Long time updating makes an initial pattern converge into one of embedded cycle attractors. Now, when we reduce connectivity r by blocking signal transfer from other neurons, then attractors gradually become unstable, and the network state changes from the embedded patterns and chaotically wanders in the state space [8, 9]. In our computer experiments, we take the connectivity to be r = 6, and, in chaotic state, apply two external inputs as (Fig. 2) [∑w _ijx _j(t) + α _i cos (2πt/S _(A,B))_i ∈ C]to the two 3 × 3 = 9 firing neurons set on the two corners (A, B), where the two periods S _(A,B) are 137 and 181, respectively. The correlation between a sending neuron and a target (receiving) neuron are calculated as shown in Fig. 3. The correlation between the sending neuron and the other neurons are calculated and shown in Fig. 3 as well.