(1)
Here,
 is the internal state of the n-th neuron,
is the internal state of the n-th neuron,  is the m-th input current, and
is the m-th input current, and  is the state of l-th readout neuron determined as
is the state of l-th readout neuron determined as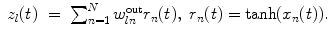
(2)
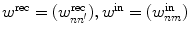 and w fb = (w nl fb) are fixed and sparsely random matrices, and only the matrix w out = (w ln out) is incrementally modified according to the recursive least square (RLS) or the gradient methods where the difference between the readout states and teacher signals is used as error signals [6].
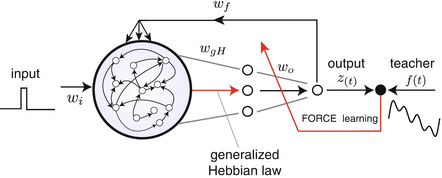
and w fb = (w nl fb) are fixed and sparsely random matrices, and only the matrix w out = (w ln out) is incrementally modified according to the recursive least square (RLS) or the gradient methods where the difference between the readout states and teacher signals is used as error signals [6].In addition to the basic structure of the FORCE-learning, we also incorporate an intermediate layer with K neurons as shown in Fig. 1, in order to (i) reduce the number of essential dimensionality of the dynamics inside the RNN and (ii) compare RNNs with different topologies (different realizations of random numbers for preparing the recurrent connectivity matrix w rec). Here, the connections between neurons in RNN and ones in the intermediate layer is incrementally updated through the “generalized Hebbian-learning (GHA)” [7] as
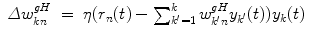
The k-th neurons y k gives the k-th principal component of the dynamics of RNN. It is expected that the dynamics of two RNNs are statistically equivalent, the readout matrices for these two RNNs are almost same against the same teacher signal. We call neural networks with the structure shown in Fig. 1 the FORCE-GHA networks in the following.
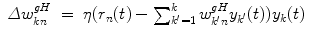
(3)

Fig. 1
Incorporation of generalized Hebbian-learning with FORCE-learning
3 Numerical Experiments and Results
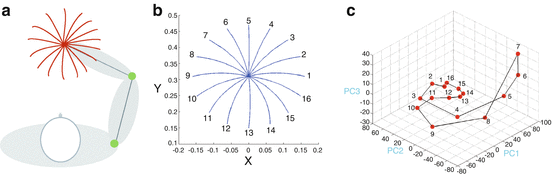
As an illustrative example of our approach, we consider generation of reaching movement patterns executed by a two-link arm (Fig. 2a) by the training of the FORCE-GHA networks. Here, the purpose of neural networks is to generate the torques u 1 and u 2 that rotate the links of an arm. In actual motor learning, the data of the torques is not directly given as teacher signals, neural networks have to acquire them in an unsupervised way such as reinforcement learning. But, this is not a main topic in this study. So, to skip this problem, we first generate arm movement trajectories using the minimum jerk principle [8] in the joint space, then obtain the torque data using the inverse model of a two-link arm used in [9]. We employ these torque data as teacher signals for the training of the FORCE-GHA networks.