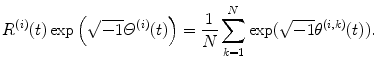or 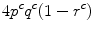 , respectively. Here, p c regulates the total number of connections in the network, q c controls the fraction of inter-modular connections among all connections in the network, and r c controls the fraction of inter-modular connections from module 1 to 2 among all inter-modular connections. Four types of oscillator-to-oscillator coupling are introduced to the network. These types of couplings lead to phase locking with 0 (in-phase), π∕2, π (anti-phase), or 3π∕2 phase lag between the two oscillators in a two-oscillator system.
, respectively. Here, p c regulates the total number of connections in the network, q c controls the fraction of inter-modular connections among all connections in the network, and r c controls the fraction of inter-modular connections from module 1 to 2 among all inter-modular connections. Four types of oscillator-to-oscillator coupling are introduced to the network. These types of couplings lead to phase locking with 0 (in-phase), π∕2, π (anti-phase), or 3π∕2 phase lag between the two oscillators in a two-oscillator system.
The dynamics of the k-th oscillator in the i-th module (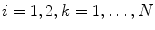 ) is described by
) is described by
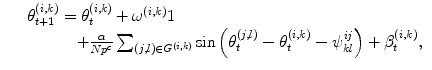 where ω (i, k) is a natural frequency, α is a coupling strength, and
where ω (i, k) is a natural frequency, α is a coupling strength, and 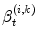 represents additive noise that affects each oscillator independently. G (i, k) represents a set of labels for those oscillators that connect to the oscillator (i, k). Each ψ kl ij is randomly assigned to one of four possible values
represents additive noise that affects each oscillator independently. G (i, k) represents a set of labels for those oscillators that connect to the oscillator (i, k). Each ψ kl ij is randomly assigned to one of four possible values 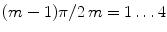 , according to probabilities
, according to probabilities 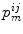 . Note that
. Note that 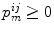 and
and 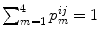 . In the case of a two-oscillator system, these couplings lead to phase locking with 0 (in-phase), π∕2, π (anti-phase), or 3π∕2 phase lag between the two oscillators. To characterize the macroscopic states of the modules, we define a phase coherence R (i)(t) and a mean phase Θ (i)(t) for each module as the absolute value and the argument of
. In the case of a two-oscillator system, these couplings lead to phase locking with 0 (in-phase), π∕2, π (anti-phase), or 3π∕2 phase lag between the two oscillators. To characterize the macroscopic states of the modules, we define a phase coherence R (i)(t) and a mean phase Θ (i)(t) for each module as the absolute value and the argument of 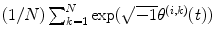 :
:
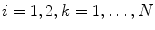 ) is described by
) is described by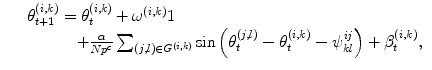
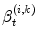 represents additive noise that affects each oscillator independently. G (i, k) represents a set of labels for those oscillators that connect to the oscillator (i, k). Each ψ kl ij is randomly assigned to one of four possible values
represents additive noise that affects each oscillator independently. G (i, k) represents a set of labels for those oscillators that connect to the oscillator (i, k). Each ψ kl ij is randomly assigned to one of four possible values 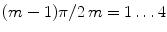 , according to probabilities
, according to probabilities 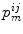 . Note that
. Note that 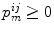 and
and 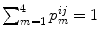 . In the case of a two-oscillator system, these couplings lead to phase locking with 0 (in-phase), π∕2, π (anti-phase), or 3π∕2 phase lag between the two oscillators. To characterize the macroscopic states of the modules, we define a phase coherence R (i)(t) and a mean phase Θ (i)(t) for each module as the absolute value and the argument of
. In the case of a two-oscillator system, these couplings lead to phase locking with 0 (in-phase), π∕2, π (anti-phase), or 3π∕2 phase lag between the two oscillators. To characterize the macroscopic states of the modules, we define a phase coherence R (i)(t) and a mean phase Θ (i)(t) for each module as the absolute value and the argument of 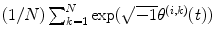 :
: