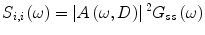(1)
for 1 ≤ i ≤ N, where v i denotes the membrane voltage of neuron i, μ is a dc component in the noisy synaptic input and τ is the membrane time constant for the subthreshold dynamics. We adopt the standard threshold-spike-reset condition [8]: a spike is emitted whenever v i (t) = V T , and after that the voltage is reset and held at v i (t +) = V R during a refractory period τ R . Additionally, s(t) is a common component in the input and the Gaussian white noise η i (t) (1 ≤ i, j ≤ N) models the internal stochastic component for the ith neuron. For each neuron, the output spike train y i (t) = ∑ k s(t − t i k ) with t i k being the kth spike time is of interest, and the average spike train
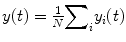 is taken as the output for summing parallel array. We assume that for 1 ≤ i, j ≤ N there is
is taken as the output for summing parallel array. We assume that for 1 ≤ i, j ≤ N there is![$$ \left\langle {\eta}_i(t){\eta}_j\left(t+\tau \right)\right\rangle =\left[{\delta}_{i,j}+c{\delta}_{i,i+1}\right]\delta \left(\tau \right) $$](/wp-content/uploads/2016/09/A315578_1_En_30_Chapter_Equ2.gif)
(2)
Since the local spatial correlation does not affect the response of each neuron, it is necessary to obtain the spectral statistics 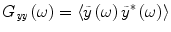 for the ensemble output spike train, where
for the ensemble output spike train, where 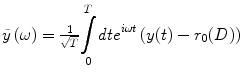 is the Fourier transform of the zero average output spike train with r 0(D) being the stationary firing rate at the noise level D. For this aim, let us resort to technique of linear approximation [9–11]. According to linear approximation, each neuron can be regarded as a linear filter, and thus the frequency domain linear response for each neuron can be approximated as
is the Fourier transform of the zero average output spike train with r 0(D) being the stationary firing rate at the noise level D. For this aim, let us resort to technique of linear approximation [9–11]. According to linear approximation, each neuron can be regarded as a linear filter, and thus the frequency domain linear response for each neuron can be approximated as
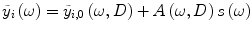
where 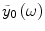 is the unperturbed part of stationary spectral density
is the unperturbed part of stationary spectral density 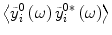 and A(ω, D) is linear susceptibility on the noise level of D. The stationary spectral density [12] and the linear susceptibility [13, 14] are explicitly given as
and A(ω, D) is linear susceptibility on the noise level of D. The stationary spectral density [12] and the linear susceptibility [13, 14] are explicitly given as
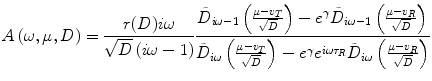
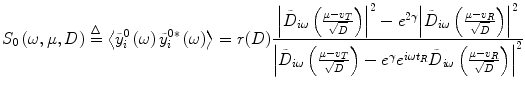
with ![$$ \gamma =\left[{v}_R^2-{v}_T^2+2\overline{\mu}\left({v}_T-{v}_R\right)\right]/4D $$](/wp-content/uploads/2016/09/A315578_1_En_30_Chapter_IEq6.gif) . And then from Eq. (3), the auto-spectral density
. And then from Eq. (3), the auto-spectral density 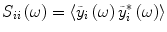 for the ith neuron is obtained as
for the ith neuron is obtained as
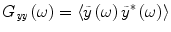 for the ensemble output spike train, where
for the ensemble output spike train, where 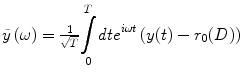 is the Fourier transform of the zero average output spike train with r 0(D) being the stationary firing rate at the noise level D. For this aim, let us resort to technique of linear approximation [9–11]. According to linear approximation, each neuron can be regarded as a linear filter, and thus the frequency domain linear response for each neuron can be approximated as
is the Fourier transform of the zero average output spike train with r 0(D) being the stationary firing rate at the noise level D. For this aim, let us resort to technique of linear approximation [9–11]. According to linear approximation, each neuron can be regarded as a linear filter, and thus the frequency domain linear response for each neuron can be approximated as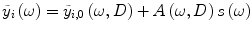
(3)
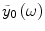 is the unperturbed part of stationary spectral density
is the unperturbed part of stationary spectral density 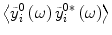 and A(ω, D) is linear susceptibility on the noise level of D. The stationary spectral density [12] and the linear susceptibility [13, 14] are explicitly given as
and A(ω, D) is linear susceptibility on the noise level of D. The stationary spectral density [12] and the linear susceptibility [13, 14] are explicitly given as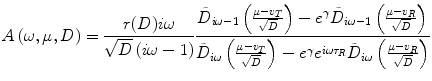
(4)
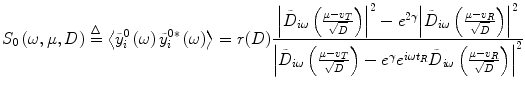
(5)
![$$ \gamma =\left[{v}_R^2-{v}_T^2+2\overline{\mu}\left({v}_T-{v}_R\right)\right]/4D $$](/wp-content/uploads/2016/09/A315578_1_En_30_Chapter_IEq6.gif) . And then from Eq. (3), the auto-spectral density
. And then from Eq. (3), the auto-spectral density 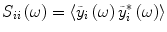 for the ith neuron is obtained as
for the ith neuron is obtained as