(1)
and covariance function
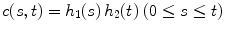 such that
such that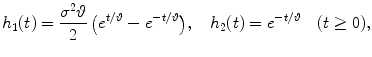
(2)
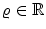 and
and 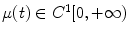 . The transition density f Y (x, t | y, τ) is a normal density with mean and variance (cf., for instance, [1, 3]):
. The transition density f Y (x, t | y, τ) is a normal density with mean and variance (cf., for instance, [1, 3]):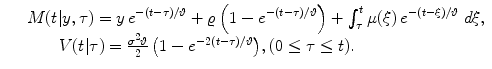
(3)
The infinitesimal moments of Y (t) are:
 .
.
Get Clinical Tree app for offline access
 .
.In the context of neuronal models, (4) characterize an inhomogeneous LIF diffusion process Y (t), describing the evolution of the membrane potential (see, for instance, [1, 8, 9]). The time constant 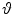 governs the spontaneous decay of the membrane potential to the resting level
governs the spontaneous decay of the membrane potential to the resting level 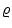 , the function μ(t) represents external signal inputs to the neuron, whereas the infinitesimal variance σ 2 gives the amplitude of the noise.
, the function μ(t) represents external signal inputs to the neuron, whereas the infinitesimal variance σ 2 gives the amplitude of the noise.
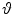 governs the spontaneous decay of the membrane potential to the resting level
governs the spontaneous decay of the membrane potential to the resting level 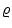 , the function μ(t) represents external signal inputs to the neuron, whereas the infinitesimal variance σ 2 gives the amplitude of the noise.
, the function μ(t) represents external signal inputs to the neuron, whereas the infinitesimal variance σ 2 gives the amplitude of the noise.In the neuronal model (4) the state space for the underlying stochastic process is the entire real axis, implying that arbitrarily large hyperpolarization values for the membrane potential are possible. Some authors (see, for instance, [4, 6, 7]) have considered alternative models by assuming the existence of a lower boundary for the membrane potential. For this reason, in the sequel, we shall focus on the Ornstein-Uhlenbeck process confined by a time-dependent reflecting boundary ν(t) that can be looked at as the neuronal reversal hyperpolarization potential.
We consider the stochastic process {X(t), t ≥ 0}, defined in the interval [ν(t), +∞), obtained by considering the Ornstein-Uhlenbeck process (4) in presence of a reflecting boundary
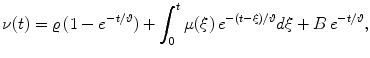
with 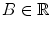 . The transition probability density function (pdf) of X(t) is (see, [4])
. The transition probability density function (pdf) of X(t) is (see, [4])
![$$\displaystyle{ f_{X}(x,t\vert y,\tau ) = f_{Y }(x,t\vert y,\tau ) + f_{Y }[2\,\nu (t) - x,t\vert y,\tau ],\quad [x \geq \nu (t),y \geq \nu (\tau )], }$$](/wp-content/uploads/2016/09/A315578_1_En_42_Chapter_Equ6.gif)
with f Y (x, t | y, τ) normal density with mean and variance given in (3).
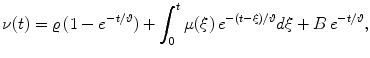
(5)
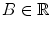 . The transition probability density function (pdf) of X(t) is (see, [4])
. The transition probability density function (pdf) of X(t) is (see, [4])![$$\displaystyle{ f_{X}(x,t\vert y,\tau ) = f_{Y }(x,t\vert y,\tau ) + f_{Y }[2\,\nu (t) - x,t\vert y,\tau ],\quad [x \geq \nu (t),y \geq \nu (\tau )], }$$](/wp-content/uploads/2016/09/A315578_1_En_42_Chapter_Equ6.gif)
(6)
We now analyze the asymptotic behavior of X(t) when the input signal μ(t) is a bounded function, asymptotically constant, i.e. 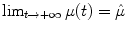 . Under such assumption, from (3) and (5) one has:
. Under such assumption, from (3) and (5) one has:
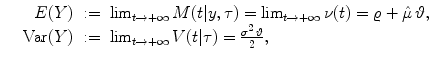 so that from (6) one obtains the steady-state pdf of the restricted Ornstein-Uhlenbeck process X(t):
so that from (6) one obtains the steady-state pdf of the restricted Ornstein-Uhlenbeck process X(t):
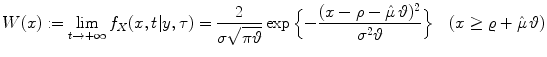 and the related asymptotic mean and variance:
and the related asymptotic mean and variance:
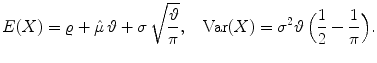 We note that
We note that 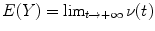 for the free Ornstein-Uhlenbeck process Y (t), whereas
for the free Ornstein-Uhlenbeck process Y (t), whereas ![$$E(X) >\lim _{t\rightarrow +\infty }\nu (t)$$
” src=”/wp-content/uploads/2016/09/A315578_1_En_42_Chapter_IEq11.gif”></SPAN> for the restricted Ornstein-Uhlenbeck process <SPAN class=EmphasisTypeItalic>X</SPAN>(<SPAN class=EmphasisTypeItalic>t</SPAN>). Furthermore, by comparing the asymptotic means and variances of <SPAN class=EmphasisTypeItalic>X</SPAN>(<SPAN class=EmphasisTypeItalic>t</SPAN>) and <SPAN class=EmphasisTypeItalic>Y</SPAN> (<SPAN class=EmphasisTypeItalic>t</SPAN>), one has <SPAN class=EmphasisTypeItalic>E</SPAN>(<SPAN class=EmphasisTypeItalic>X</SPAN>) > <SPAN class=EmphasisTypeItalic>E</SPAN>(<SPAN class=EmphasisTypeItalic>Y</SPAN> ) and Var(<SPAN class=EmphasisTypeItalic>X</SPAN>) < Var(<SPAN class=EmphasisTypeItalic>Y</SPAN> ).</DIV><br />
<DIV class=Para>We now consider the first passage time (FPT) problem to a threshold <SPAN class=EmphasisTypeItalic>S</SPAN>(<SPAN class=EmphasisTypeItalic>t</SPAN>) > <SPAN class=EmphasisTypeItalic>ν</SPAN>(<SPAN class=EmphasisTypeItalic>t</SPAN>), with <SPAN class=EmphasisTypeItalic>S</SPAN>(<SPAN class=EmphasisTypeItalic>t</SPAN>) ∈ <SPAN class=EmphasisTypeItalic>C</SPAN> <SUP>1</SUP>[0, +<SPAN class=EmphasisTypeItalic>∞</SPAN>), for the restricted Ornstein-Uhlenbeck process, with reflecting boundary <SPAN class=EmphasisTypeItalic>ν</SPAN>(<SPAN class=EmphasisTypeItalic>t</SPAN>) given in (<SPAN class=InternalRef><A href=]() 5). We denote by
5). We denote by
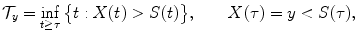 the random variable FPT of X(t) from
the random variable FPT of X(t) from 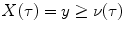 to the threshold S(t) and by
to the threshold S(t) and by
![$$\displaystyle{g_{X}[S(t),t\vert y,\tau ] = \frac{\partial } {\partial t}P{\bigl (\mathcal{T}_{y} \leq t\bigr )}\qquad [\nu (\tau ) \leq y < S(\tau )]}$$](/wp-content/uploads/2016/09/A315578_1_En_42_Chapter_Equd.gif) its FPT pdf. In the neuronal modeling context, g X [S(t), t | y, τ] identifies the firing density of X(t), i.e. the FPT pdf of X(t) through the firing threshold S(t) starting from y at time τ.
its FPT pdf. In the neuronal modeling context, g X [S(t), t | y, τ] identifies the firing density of X(t), i.e. the FPT pdf of X(t) through the firing threshold S(t) starting from y at time τ.
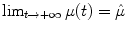 . Under such assumption, from (3) and (5) one has:
. Under such assumption, from (3) and (5) one has: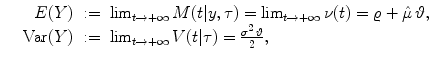
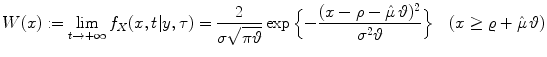
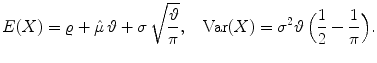
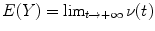 for the free Ornstein-Uhlenbeck process Y (t), whereas
for the free Ornstein-Uhlenbeck process Y (t), whereas 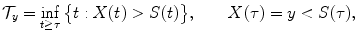
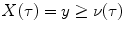 to the threshold S(t) and by
to the threshold S(t) and by![$$\displaystyle{g_{X}[S(t),t\vert y,\tau ] = \frac{\partial } {\partial t}P{\bigl (\mathcal{T}_{y} \leq t\bigr )}\qquad [\nu (\tau ) \leq y < S(\tau )]}$$](/wp-content/uploads/2016/09/A315578_1_En_42_Chapter_Equd.gif)
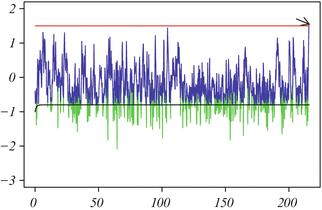
Figure 1 shows two simulated sample paths for the free process Y (t) (green) and for the restricted process X(t) (blue), both obtained via an appropriate algorithm based on the simulation of the Brownian motion in the presence of a constant reflecting boundary and on suitable spatio-temporal transformations (the details of the algorithm are object of our paper in preparation). The arrow in Fig. 1 indicates the instant of the first passage time. The firing pdf g X [S(t), t | y, τ] is solution of the nonsingular Volterra integral equation (see, [4])