(1)
Department of Neurology, Wake Forest University School of Medicine, Winston-Salem, NC, USA
Abstract
This chapter presents definitions and important multi-domain concepts involved in the design and operation of dependable systems. It presents the dependability tree and describes the means to attain dependability. It presents the ideas of fault detection, fault tolerance, fault handling, and fault removal which form the basis of all dependable systems. It surveys common safety paradigms across multiple industries from a standards and regulatory perspective. It introduces the concept of defense in depth as the means of attaining safety and dependability.
Keywords
DependabilityDependability treeReliabilitySafetyFault preventionFault toleranceFault maskingFault removalFault forecastingSystem validation and verificationReliability curveMulti-domain safetySafety integrity levels (SIL)AviationSpaceRailwayNuclear safetyDefense in depthBaruch SpinozaDefinition of Dependability
An important concept in industry and engineering is dependability [1]. At an intuitive level, we use the word “dependable” to refer to a product or service which we take for granted. Therefore, from our understanding, a dependable service is always available, trustworthy, reliable, and most importantly, safe. The world of airplanes, high-speed trains, telephones, and highly networked and sophisticated computers managing vital services like the power grid and traffic systems are common examples of dependable systems. These systems are special because errors can have catastrophic consequences with the potential for severe injuries and loss of life. By application of rigorous, disciplined, engineering and management methods, industries such as aerospace, high-speed rail, and to a great extent, nuclear power have attained extremely safe operating characteristics. An unsafe event is extremely rare with probabilities of serious accidents being less than one in one billion. This book explores the ideas behind dependable systems and businesses and applies them to healthcare delivery by using a wide range of case examples from the field of neurology in particular.
Let us now explore more rigorous definitions of the concept, its standards, and regulatory framework. In computer science parlance, dependability can be defined as “a system property that integrates such attributes as reliability, availability, safety, security, survivability, and maintainability [1].” Standards of performance and dependability vary widely between different industries. The most rigorous definitions and standards of dependability were developed for the aerospace industry with digital fly-by wire (DFBW) being one of the most exacting applications. In other domains such as medicine, such standards are not well-defined, neither are the methods which contribute to dependability in widespread application. The principles behind dependability are both technological and human, the successful integration of which creates iconic businesses and products.
A Brief History of Evolution of Dependable Systems
The delivery of correct, reliable systems has been a concern since time immemorial. Mathematicians and statisticians working with computing engines struggled with this concept. In 1834, Dr. Dionysius Lardner wrote in the Edinburgh Review “the most certain and effectual check upon errors which arise in the process of computation, is to cause the same computations to be made by separate and independent computers; and this check is rendered still more decisive if they make their computations by different methods [1].”
Systems have a tendency to generate errors and service failure. Dependable systems must constantly overcome these challenges and have a method for keeping errors and faults in check. The earliest challenges with dependability were encountered with the advent of the electronic age. Early electronic components and circuits were unreliable. Since component-wise reliability was poor, the problem became one of how to deliver dependable performance with systems with unreliable components? The solution lay in redundancy. The field developed enormously with the digital age and development of information theory by Claude Shannon. At the heart of most of these methods, redundancy is incorporated to detect and correct errors. This can take the form of triple redundant voting architectures developed by John von Neumann [1] or error correcting codes in digital communications where a message of k bits is encoded using N bits (where N > k) to provide for error detection and correction. Dependable systems detect errors; isolate them followed by masking errors so that service delivery is not disrupted. The theory of redundancy to mask individual component failures was developed by W. H. Pierce in the early 1960s. The field was further developed by the pioneering work of Prof. Algirdas Avizienis with the development of fault tolerant systems. This section is based on a review paper by Avizienis et al. [1]. Overview concepts will be discussed here, the interested reader will find a wealth of further information in [1].
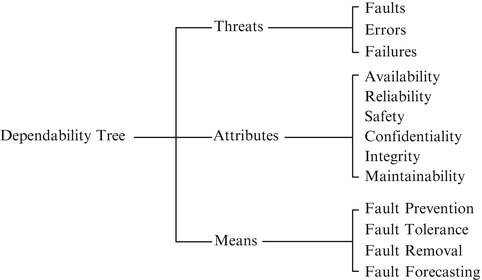
The Dependability Tree
The dependability tree is a useful concept for understanding the nature of dependability. The dependability tree studies the subject from the viewpoint of threats to, attributes of and means by which dependability is attained. While the original application of this is in computing, these concepts can be borrowed and applied widely and other processes can be understood in the same manner with potential advantages to dependability. Let us start with some definitions. For a computer system, dependability is the ability to deliver service that can be justifiably trusted by the user [1]. From the dependability tree in Fig. 1.1, the main threats to dependability are faults, errors, and failures. An error is that part of a system state that may result in subsequent failure. Errors may be manifest or maybe latent. A failure happens when an error alters service. A fault is the cause of an error. Therefore faults can lead to errors which lead to failures. The ways in which a system can fail are its failure modes [1].
Toy Example 1: Consider a commonly encountered situation where a patient with atrial fibrillation and mechanical heart valve is on a stable dose of warfarin for many years for stroke prevention. He maintains therapeutic INR for stroke prevention. At a subsequent hospitalization, a physician enters the wrong dose of warfarin or adds a medicine (for example an antiepileptic such as carbamazepine) that interacts with warfarin and increases its hepatic metabolism. This reduces the therapeutic effect of warfarin leading to a subtherapeutic INR which leads to an embolic stroke. In this example, the wrong dose entered or the drug interaction is the initiating “fault.” This led to an altered coagulation system state with reduced therapeutic effect which represents the “error.” The subtherapeutic anticoagulation (“error”) leads to a “failure” of the service of stroke prevention provided by warfarin.
Let us explore the meaning of attributes of dependability further. The availability of a service is the readiness for correct service. Reliability refers to continuous delivery of correct service or time to failure. In the computer science literature this is also defined as “probability of failure free operation of a computer program in a specified environment for a specified period of time” [2, 3]. Safety is the absence of catastrophic consequences of failures on the user or environment. Confidentiality is the absence of unauthorized disclosure of information. Integrity is the absence of improper system state alterations. Maintainability is the ability to undergo repairs and modifications. The emphasis on the different attributes varies from industry to industry and the intended service provided by the system. A system is expected to have dependability requirements imposed on it. A system’s reactions to faults, whether internal or external is important and is a measure of the robustness of the system.
Applying this concept to healthcare, our goal is to borrow from planes, trains, and computers to create a dependable medical practice, whether in the form of a clinic or a hospital. From a patient or user’s perspective, the services provided by the hospital or practice must be reliably trustworthy. Services must be readily available, of high quality. Diagnosis must be accurate, treatment must be safe without errors and at a minimum of side effects. To this we borrow and add one more requirement, frequently overlooked in healthcare but a core component of all industrial projects—costs must be optimum and transparent. Therefore, dependable healthcare, emulating the world of like products and services in engineering provided by our dependable institution must provide service that can be reliably trusted by the user in terms of diagnostic accuracy, optimum treatment, and costs.
Approach to Dependability
From the “means” arm of the dependability tree in Fig. 1.1, the design of a dependable system involves four important aspects [1]:
1.
Fault prevention: refers to the application of design and operating principles that prevent the occurrence of faults.
2.
Fault tolerance: refers to the ability of the system to deliver correct service in the presence of faults.
3.
Fault removal: refers to reducing the number and severity of faults.
4.
Fault forecasting: refers to predicting and addressing present and foreseeable faults and their consequences.
Fault Prevention
Fault prevention is concerned with primary prevention—incorporating methodologies and technologies in design and operations which prevent the introduction of faults [2]. At the design level, this involves quality control measures involved in design and manufacturing. On a day-to-day basis, this involves safe operating practices including rigorous training, adherence to standards, operating protocols, and maintenance guidelines. For the toy example above, fault prevention can be instituted in design where the electronic medical record would generate multiple severe warnings when the interacting drugs are prescribed warning the physician to potential dangers. At the human level, fault prevention includes rigorous training, familiarity with antiepileptics, or verification of dose and interactions with a pharmacist so that safer alternatives can be selected. Finally, fault prevention could also involve close monitoring of INR if the physician chooses to use medications that interact with warfarin.
Fault Tolerance
Fault tolerance refers to the ability to deliver correct service in the presence of active faults in the system [1]. The aim of fault tolerance is to prevent undesirable events, especially catastrophic failure in the presence of faults affecting individual parts of a system [1, 2]. In other words, a single failure of a system or a combination of failures should not lead to service failure, especially catastrophic failure. A latent fault is a fault that is present in the system but has not resulted in errors. These represent a vulnerability of the system. Once errors occur due to these vulnerabilities, a latent fault becomes active [2].
Fault tolerant systems integrate fault masking with practical techniques for error detection, fault diagnosis, and system recovery [1]. Masking refers to the dynamic correction of errors which enables the system to continue to deliver correct service in the face of system faults. While the following discussion is borrowed from the computer science and engineering literature, the aim is to introduce the concepts for broader application. As introduced earlier, the basis of all fault tolerance is appropriate use of redundancy to mask faults, errors, and continued delivery of correct service [1]. Diversity in design is believed to be the “best protection against uncertainty” [2]. Fault tolerance is frequently implemented by error detection and subsequent system recovery [1]. Every fault tolerant system design involves implementation of the following principles [1, 2]:
Error detection: Error detection is the first step in the prevention of system failure. All fault tolerant systems must have a means for error detection. For the toy example above, careful monitoring of the INR to monitor for drug interactions would have detected the error in anticoagulation and prevented the hazardous failure (stroke).
System recovery: It is the transformation of a system from a state which contains one or more errors and possibly faults into a state without detected errors and faults that can be activated again [1]. The process of recovery involves error handling and fault handling.
1.
Error handling: The goal of error handling is to eliminate errors from the system state. This can be done in three ways [1, 2].
Rollback: This is a state transformation where the system is returned back to a saved state that existed prior to error detection, the saved state being called a checkpoint. For the toy example above, this would involve discontinuing the carbamazepine and resuming the last known effective dose of warfarin.
Compensation: Refers to a situation where the erroneous state contains enough redundancy to enable elimination of errors. This can happen without explicit concomitant error detection and correction in fault masking. However simple masking without correcting the underlying errors and faults can conceal a progressive and eventually catastrophic loss of protective redundancy. Therefore most practical implementations of masking generally involve error detection and fault handling [1, 2]. For the toy example above, let us assume that the patient has an INR checked a few days later (but before the stroke) which is found to be subtherapeutic. Let us also assume the patient continues to be on carbamazepine for seizure prophylaxis. The physician immediately institutes adjunct treatment with low molecular weight heparin injections (example enoxaparin or fondaparinux) which restores anticoagulation and corrects the error in the anticoagulation state. This would be an example of masking where redundancies in drugs that work on the coagulation cascade are used to deliver the service of anticoagulation and prevent service failure (in this instance stroke).
Rollforward: Where a state without detected errors is the new state [1].
2.
Fault handling: Prevents located faults from being activated again. It involves four steps:
Fault diagnosis: The faulty components are identified, isolated, and the effects contained for system repair. This identifies the root cause(s) of the error(s) [1]. In the toy example, this would involve identifying responsible drug interaction (or wrong dose) as the fault that led to the error which led to the stroke.
Fault isolation: Involves physical or logical exclusion of the faulty components from further participation in service delivery. The diagnosed fault becomes dormant [1]. For the example above, this would imply a decision not to rely on the warfarin pathway for delivering dependable anticoagulation. Errors in systems must be contained within predetermined boundaries. This is enabled by modular design of systems and the ability to isolate a faulty system to prevent it from propagating errors. Failure to do so leads to cascading failure with far reaching consequences as discussed in toy example 1. In that example, a fault in warfarin led to the error in the state of anticoagulation which led to the development of a clot in the left atrium (cardiovascular system) which migrated to the brain causing a stroke (central nervous system).
System reconfiguration: This involves finding ways to work around faults by removing affected systems from operation and incorporating alternate means to deliver service. For the toy example above, the physician can explore alternative methods, including low molecular weight heparins or direct thrombin inhibitors for service delivery. Alternate options include switching to an antiepileptic such as levetiracetam (Keppra) which is renally metabolized and therefore free from interactions with warfarin.
System reinitialization: This step checks, updates, and records the new configuration and updates system records [1]. For the toy example above, the new state maybe resuming prior dose of warfarin, discontinuing carbamazepine, temporary use of low molecular weight heparins, and instituting levetiracetam for seizure prophylaxis.
Fault handling is typically followed by corrective maintenance that removes the faults isolated by fault handling. This may take diverse forms including equipment replacement or repair [1]. Dependable systems that are designed to fail only in specific modes and only up to an acceptable extent are called fail-controlled systems [1]. A system whose failures are to a great extent minor is called a fail-safe system [1].
Fault tolerance can be studied from both software and hardware perspectives. One of the most common methods used for fault tolerance is to perform multiple computations in multiple different channels either sequentially or concurrently [1, 2]. (See reference to Dr. Lardner in Section “A Brief History of Evolution of Dependable Systems”). Multi-version fault tolerance techniques are a commonly used method to deliver fault tolerance. This method is based on the use of two or more versions of software usually executed in parallel. The idea behind this approach is that different versions of software will use different components and algorithms. Since failures usually result from a certain combination of system states and input data, it is believed that different versions would fail under different circumstances [2, 4]. Therefore, a given input pattern which could provoke failure in one system may not do so in the other enabling delivery of service. This can be performed in different ways and two widely used architectures are presented here.
1.
One commonly implemented method for multi-version fault techniques is N–version programming. In this technique multiple versions perform computations in parallel and the outputs are compared by voting as shown in Fig. 1.2 [2]. Similar architectures are exploited in hardware. Triple modular redundancy (TMR) is a commonly used fault tolerance architecture with applications in diverse industries ranging from aerospace to industrial automation. This is the architecture used in the Boeing 777 primary flight computer (PFC) system and will be discussed further in Chap. 6. The output from the three modules is compared by the voter. The system is capable of discarding error from one module by performing majority voting of the individual outputs. The fault masking capabilities of the system fail when an error occurs in two or more modules such that a majority vote is no longer valid. The system is additionally susceptible to voter failure [2]. This can be circumvented to some extent by triplicating the voting system so that individual voter failures can be masked by the same process. Additional protections are made in the design and manufacturing process such that the voter has a much greater degree of reliability than the rest of the system to prevent system failure.
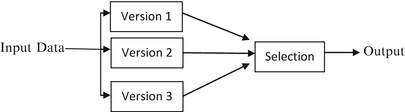

Fig. 1.2
N-version Programming model
2.
In duplication by comparison shown in Fig. 1.3, errors are detected by comparing the outputs of the two modules. If the outputs disagree by more than a predetermined threshold, an error condition is raised followed by diagnosis and restoration of the system to error free operation. The two systems are designed by two different teams working independently and manufactured by different manufacturers to avoid any common software and hardware vulnerabilities. This architecture is also used widely and will be discussed further in the Airbus fly-by wire system.


Fig. 1.3
Active redundancy using duplication by comparison
Fault Removal
Fault removal is performed both during the development phase of a system life cycle and during its operational life [1]. In this section we expand the lexicon further by introducing two commonly encountered terms—validation and verification. System validation refers to confirming that the system being designed meets the user’s requirements, needs, and uses. In other words, we are creating the system that the user wants [1]. System verification refers to whether the outputs of the system conform to the specifications [2]. In other words, verification tests whether the system has been designed correctly to meet the requirements placed on it.
As an example, consider that an aircraft manufacturer wants to develop a new model of airplane which can carry 200 passengers for a distance of 5,000 miles and wants a dependable engine with specified downtimes for maintenance. The engine manufacturer comes up with an initial design which would deliver x lbs. of thrust, y kg/seat mile of fuel economy, etc. System validation involves checking that such an engine meets the customer’s intended uses and specifications. The hope of the validation process is to identify early in the process if x lbs. of thrust are sufficient for the application or whether the design should be changed to deliver additional z lbs. of thrust before expensive investments in manufacturing the engine are made. System verification would test the engine that is being designed and manufactured to see if it will deliver the required x lbs. of thrust and required fuel economy under diverse operating conditions.
System validation and verification are recursive processes which are extremely important for delivering dependability. This is best done throughout the design process instead of creating a product and then performing expensive re-engineering to meet customer expectations. Fault removal occurs throughout the life cycle of a system [1]. In the development phase fault removal consists of three steps: verification, diagnosis, and correction. System verification continuously determines whether the system meets design properties which are termed verification conditions. If the system does not meet the desired properties, the next step is to diagnose the faults which prevented the verification conditions from being met. Fault identification is followed by necessary corrections. The verification process is again repeated to check that the preceding fault removal did not cause any unintended consequences. In software parlance, fault prevention and fault removal are termed fault avoidance. Fault removal during the operational life of a system is termed corrective or preventive maintenance. Corrective maintenance is performed to remove faults that have produced error(s) and have been diagnosed. Preventive maintenance aims to uncover and remove faults before they cause errors during normal operation [1].
Fault Forecasting
Fault forecasting involves evaluating system behavior for the occurrence and activation of faults. This is used to prevent faults in future. This involves two steps—qualitative evaluation and quantitative evaluation. Qualitative evaluation aims to identify, classify, and rank the different ways in which a system can fail, termed failure modes. It identifies the event combinations (component failures or environmental conditions) that lead to system failures [1]. Methods for qualitative evaluation include failure modes and effects analysis (FMEA) and others which will be studied in subsequent chapters. Quantitative methods evaluate probability measures of how attributes of dependability are satisfied thus providing a measure of dependability of a system [1]. Methods such as fault tree analysis (FTA) and reliability block diagrams (RBD) which can be both qualitative and quantitative are explored in detail in subsequent chapters [1].
Failure Intensity and Lifecycle of Dependable Systems
The life cycle of most typical dependable systems is characterized by alternate periods of correct and incorrect service delivery. A useful index of this principle is failure intensity—which is the number of failures per unit of time. Typically, failure intensity decreases as more common faults are discovered and corrected (period termed reliability growth), then stabilizes (stable reliability) followed by a period of decreased reliability followed by repetition of the cycle. This is usually pictured as a “bathtub,” see Fig. 1.4.
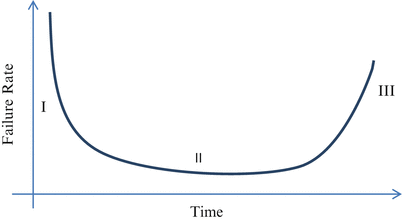

Fig. 1.4
The reliability curve also called “bathtub curve” represents the failure rate of a system vs. time. There are three regions in this curve. Region I constitutes a time of high failure rates when a component is initially manufactured. As design flaws and manufacturing processes are corrected, the failure rate drops in Region II to a flat constant failure rate. Finally as the component ages and starts wearing out in Region III, the failure rate again increases
Important measures of reliability, especially in engineering are mean time between failures (MTBF), mean time to failure (MTTF), and mean time to repair (MTTR) [3]. These are connected by the expression:
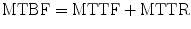
This is illustrated in Fig. 1.5. MTTF is a measure of how long a system is expected to deliver correct service before failure occurs. MTTR is a measure of how easy or difficult it is to repair a system after a failure occurs. In computer controlled systems, advances in software engineering have reduced the number of deterministic design faults. More difficult to control are latent faults in software and hardware which are state dependent and activated by a particular set of input data and operating conditions [2]. These are highly unpredictable since a system crash is triggered by a specific set of input data which exposes a unique, hidden vulnerability in software and hardware resulting in service failure which may not have been foreseen during system development and testing. Therefore, a latent fault in software and hardware becomes activated when the system state and triggering input sequences come together. Therefore, for many systems, MTTF is dependent on the operating environment. As introduced earlier, this is mitigated in dependable systems by incorporating redundant systems using different hardware and software which very likely have a very different set of state and input vulnerabilities and therefore do not crash under the same circumstances.

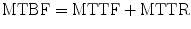
(1.1)

Fig. 1.5
In this figure, solid lines represent normal system function and dashed line represents failure. A system starts operation and performs without failure till point A. The time interval T1 is defined as the time to first failure or reliability. The dashed line represents the time when the system is not available with consequent service failure. It undergoes repair during this time (T2), starts functioning again at point B before failing at time C (T3) before the cycle repeats itself. The time T2 is the time to repair followed by time to failure. Therefore, the time interval between A and C which represents the time between failures can be seen to be the time to repair (T2) + time to failure (T3). Over repeated cycles, mean times can be used to compute the mean time between failures in Eq. (1.1).
The same is applicable to medical knowledge as well. Medical education is verified and validated by rigorous curricula and board certification examinations. However, all knowledge is imperfect and there are regions of vulnerability in each individual’s understanding of health and disease. A hidden, unique vulnerability in a physician or healthcare worker’s knowledge is challenged by a rare, unique clinical circumstance leading to errors in diagnosis and treatment. As in the systems engineering example, redundancy can be used to deliver dependability. The knowledge redundancy is delivered using teamwork, second opinions, and concurrent opinions so that one individual’s unique knowledge vulnerability in a certain clinical situation is masked by another’s strength leading to fault prevention, fault masking, and correct service delivery despite individual failure.
Connected Systems and Failure
Most products and services are made of component systems which in turn are made of subsystems in a hierarchical relationship. Systems communicate with one another across system boundaries. In many failures, a fault in one system leads to an error which is propagated across system boundaries to affect many systems leading to profound effects remote from the initial source. At the interface between System 1 and System 2, an error in System 1 is a fault in System 2. By the time the initial error is detected and corrected, the downstream effects are only too well established and emerge as the major problem. Such error cascades are quite common and can have far reaching, sometimes catastrophic consequences. The failure cascade described in Fig. 1.6 is frequently encountered in clinical practice due to the lack of a disciplined approach to system safety and dependability. The following case example is illustrative:
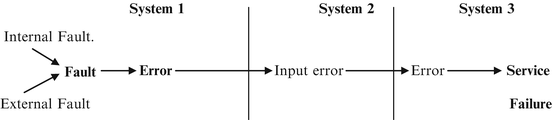

Fig. 1.6
The relation between fault, errors, and failure. A fault in System 1 leads to errors in System 1 which is propagated to System 2. At the interface, the error in System 1 is a fault in System 2 which can lead to a corresponding error. This finally results in failure of service in System 3
Case Example 1
G.S. is a 70-year-old male, s/p pacemaker placement, on anticoagulation with a prior biopsy proven diagnosis of polymyositis. He had been treated with varying doses of prednisone with poor response to treatment. Patient himself provided a limited history but it appears his muscle disease started fairly abruptly after undergoing coronary artery bypass grafting (CABG). Weakness was rapidly progressive leading to difficulty with ambulation in short order. Over the past few years he developed dysphagia. It was not clear if symptoms were related to statin exposure. A review of his biopsy did not show rimmed vacuoles concerning for inclusion body myositis (IBM), however this might have been due to sampling error. He denied any family history of muscular dystrophy. On examination, he had moderate bifacial weakness being unable to whistle. Extraocular movements were otherwise normal. He had severe weakness and wasting of pectoralis major and scapular muscles. Scapular winging was present bilaterally. There was relative preservation of the deltoids bilaterally which were 3+/5. There was severe wasting of the biceps and triceps bilaterally. The wrist extensors were 4/4 bilaterally, the wrist flexors were similar. Patient was unable to make a fist bilaterally with the weakness of flexor pollicis longus (FPL) and deep finger flexors. Hand intrinsics were normal. In the lower extremities hip flexors, knee extensors showed only trace strength. Foot dorsiflexors were 3+/5, plantar flexors were 4/5. At the time of his initial visit, he was on prednisone 10 mg/day for many years.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree