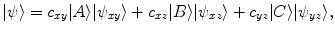,  , and
, and  , whose dynamics are given by
, whose dynamics are given by
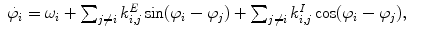
(1)
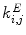 and
and 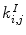 are the overall excitatory and inhibitory couplings between the neural oscillators. During reinforcement, the coupling strengths
are the overall excitatory and inhibitory couplings between the neural oscillators. During reinforcement, the coupling strengths 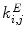 and
and 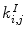 are changed in a Hebb-like fashion. This model can easily be extended to include multiple stimulus and response oscillators. For instance, in [3] it was used with two stimulus oscillators to obtain quantum-like effects. Such effects were the consequence of couplings between the oscillators that were reinforced to respond to two different stimuli corresponding to incompatible contexts. When both stimuli were simultaneously activated, an interference effect was obtained.
are changed in a Hebb-like fashion. This model can easily be extended to include multiple stimulus and response oscillators. For instance, in [3] it was used with two stimulus oscillators to obtain quantum-like effects. Such effects were the consequence of couplings between the oscillators that were reinforced to respond to two different stimuli corresponding to incompatible contexts. When both stimuli were simultaneously activated, an interference effect was obtained.Quantum-like models lead to contextual responses, in the sense that there exists no joint probability distribution for the associated random variables. Let us look at the particular example presented in reference [2] and expanded in another context in [5]. Let 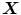 ,
, 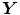 , and
, and 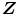 be ± 1-valued random variables, and consider the neural oscillator system represented in Fig. 1.
be ± 1-valued random variables, and consider the neural oscillator system represented in Fig. 1.
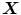 ,
, 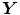 , and
, and 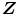 be ± 1-valued random variables, and consider the neural oscillator system represented in Fig. 1.
be ± 1-valued random variables, and consider the neural oscillator system represented in Fig. 1.
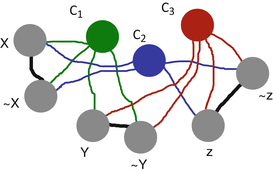
Fig. 1
Layout of a neural-oscillator system exhibiting pairwise correlations between 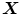 ,
, 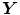 , and
, and 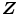 . In this oscillator system,
. In this oscillator system, 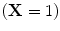 and
and 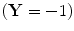 corresponds to the synchronization with oscillator C 1 closer in phase to X and not to
corresponds to the synchronization with oscillator C 1 closer in phase to X and not to 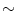 X, while at the same time being closer to Y than to
X, while at the same time being closer to Y than to 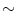 Y
Y
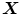 ,
, 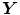 , and
, and 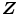 . In this oscillator system,
. In this oscillator system, 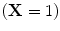 and
and 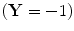 corresponds to the synchronization with oscillator C 1 closer in phase to X and not to
corresponds to the synchronization with oscillator C 1 closer in phase to X and not to 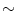 X, while at the same time being closer to Y than to
X, while at the same time being closer to Y than to 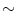 Y
Y For this system, the activation of one of the three stimulus oscillators, C 1, C 2, or C 3, leads to the corresponding responses computed via phase differences. For example, if C 1 is sampled, the oscillators’ dynamics, dictated by the specific values of inhibitory and excitatory couplings, converge to a fixed point that may favor X = 1 (oscillator X) instead of 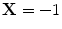 (oscillator
(oscillator 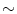 X), while at the same time favoring Y = −1, thus corresponding to a negative correlation. With such oscillator system, it is possible in principle to choose couplings such that the correlations between
X), while at the same time favoring Y = −1, thus corresponding to a negative correlation. With such oscillator system, it is possible in principle to choose couplings such that the correlations between 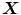 ,
, 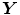 , and
, and 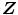 are too strong for a joint probability distribution to exist. As a consequence, and because of the pairwise commutativity of the set of quantum-mechanical observables
are too strong for a joint probability distribution to exist. As a consequence, and because of the pairwise commutativity of the set of quantum-mechanical observables 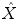 ,
, 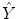 , and
, and 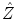 corresponding to the random variables
corresponding to the random variables 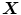 ,
, 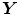 , and
, and 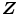 , it follows that there exists no state
, it follows that there exists no state 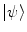 in the Hilbert space
in the Hilbert space 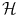 where such observables are defined and such that the neural correlations hold [5]. However, even in such situations a quantum model can be constructed [1], and in order to describe the correlations set by the neural-oscillator model, we are forced to expand the Hilbert space to
where such observables are defined and such that the neural correlations hold [5]. However, even in such situations a quantum model can be constructed [1], and in order to describe the correlations set by the neural-oscillator model, we are forced to expand the Hilbert space to 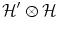 [5]. For instance, we can write a state vector
[5]. For instance, we can write a state vector
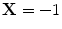 (oscillator
(oscillator 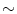 X), while at the same time favoring Y = −1, thus corresponding to a negative correlation. With such oscillator system, it is possible in principle to choose couplings such that the correlations between
X), while at the same time favoring Y = −1, thus corresponding to a negative correlation. With such oscillator system, it is possible in principle to choose couplings such that the correlations between 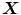 ,
, 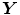 , and
, and 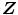 are too strong for a joint probability distribution to exist. As a consequence, and because of the pairwise commutativity of the set of quantum-mechanical observables
are too strong for a joint probability distribution to exist. As a consequence, and because of the pairwise commutativity of the set of quantum-mechanical observables 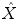 ,
, 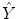 , and
, and 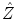 corresponding to the random variables
corresponding to the random variables 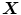 ,
, 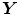 , and
, and 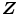 , it follows that there exists no state
, it follows that there exists no state 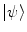 in the Hilbert space
in the Hilbert space 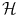 where such observables are defined and such that the neural correlations hold [5]. However, even in such situations a quantum model can be constructed [1], and in order to describe the correlations set by the neural-oscillator model, we are forced to expand the Hilbert space to
where such observables are defined and such that the neural correlations hold [5]. However, even in such situations a quantum model can be constructed [1], and in order to describe the correlations set by the neural-oscillator model, we are forced to expand the Hilbert space to 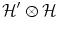 [5]. For instance, we can write a state vector
[5]. For instance, we can write a state vector