. The spins recorded in each trial are realizations of random variables A and B, which, in the simplest case, can attain two values each: a 1 or a 2 for A and b 1 or b 2 for B. One can think of many examples in other domains with similar formal structure, e.g., a psychophysical experiment with an observer responding to stimuli with varying characteristics α (say, intensity) and β (say, shape). These characteristics then constitute inputs, while some characteristics of the responses, such as response time A (with a continuum of values) and response correctness B (with two possible values), are random outputs.
Accounts of the approach presented in this paper can be found in [5–7], but this paper is the first one focusing entirely on its basic principles. The approach amounts to philosophical rethinking (or at least conceptual tweaking) of the foundations of probability, specifically, of random variables and their joint distributions. Here, it is presented without technical details (that can be reconstructed from [3–6]).
2 Basic Principles
Let all or some of the random outputs of a system form a random variable X,1 and the totality of all inputs be a variable χ. In our target example,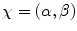 
with input values 
, …, 
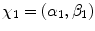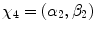, whereas X can be 
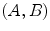with values 
, …, 
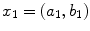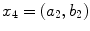, or A with values a 1, a 2, or B with values b 1, b 2. If χ itself is a random variable, so that χ 1, χ 2, … occur with some probabilities, we ignore these probabilities and simply condition the recorded outputs X on values of χ. In other words, we have a distribution of X given that χ = χ 1, a distribution of X given that χ = χ 2, etc., irrespective of whether we can control and predict the values of χ, or they occur randomly. Now, this conditioning upon input values means that X is indexed by different values of χ. We obtain thus, “automatically,” a set of different random variables in place of what we previously called a random variable X. We have 
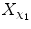(or X 1, if no confusion is likely) which is X when χ = χ 1, 
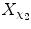(or X 2) which is X when χ = χ 2, etc. Let us formulate this simple observation as a formal principle.
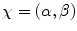with input values 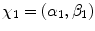, …, , 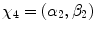whereas X can be 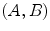with values 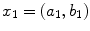, …, , 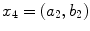or A with values a 1, a 2, or B with values b 1, b 2. If χ itself is a random variable, so that χ 1, χ 2, … occur with some probabilities, we ignore these probabilities and simply condition the recorded outputs X on values of χ. In other words, we have a distribution of X given that χ = χ 1, a distribution of X given that χ = χ 2, etc., irrespective of whether we can control and predict the values of χ, or they occur randomly. Now, this conditioning upon input values means that X is indexed by different values of χ. We obtain thus, “automatically,” a set of different random variables in place of what we previously called a random variable X. We have 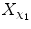(or X 1, if no confusion is likely) which is X when χ = χ 1, 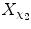(or X 2) which is X when χ = χ 2, etc. Let us formulate this simple observation as a formal principle.Principle 1
Outputs recorded under different (hence mutually exclusive) input values are labeled by these input values and considered different random variables. These random variables are stochastically unrelated, i.e., they possess no joint distribution.
Thus, in our target example, we have four random variables A ij , four random variables B ij , and four random variables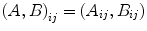 
corresponding to the four input values 
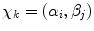. The principle holds irrespective of how the distribution of X k depends on χ k . Thus, the variables A i1 and A i2 remain different even if their distributions are identical (as they should be if Bob’s choice cannot influence Alice’s measurements). One must not assume that they are one and the same random variable, 
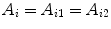. The latter would mean that A i1 and A i2 have a joint distribution, because of which the probabilities ![$$\Pr \left [A_{i1} = A_{i2}\right ]$$](/wp-content/uploads/2016/09/A315578_1_En_57_Chapter_IEq13.gif)
are well defined, and that these probabilities equal 1. But A i1 and A i2 do not have a joint distribution. Indeed, two random variables X and Y have a joint distribution only if their values can be thought of as observed “in pairs,” i.e., if there is a scheme of establishing correspondence 
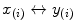between observations 
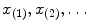of X and 
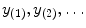of Y. In our example, the correspondence is defined by the two measurements being simultaneously performed on a given pair of entangled particles. Each such a pair of measurements corresponds to a certain input value, e.g., A 21 and B 21 correspond to 
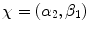. Therefore, no measurement outputs corresponding to different input values, such as A i1 and A i2, or A i1 and B i2 co-occur in the same sense in which, say, A i1 co-occurs with B i1.
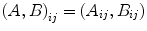corresponding to the four input values 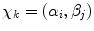. The principle holds irrespective of how the distribution of X k depends on χ k . Thus, the variables A i1 and A i2 remain different even if their distributions are identical (as they should be if Bob’s choice cannot influence Alice’s measurements). One must not assume that they are one and the same random variable, 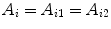. The latter would mean that A i1 and A i2 have a joint distribution, because of which the probabilities are well defined, and that these probabilities equal 1. But A i1 and A i2 do not have a joint distribution. Indeed, two random variables X and Y have a joint distribution only if their values can be thought of as observed “in pairs,” i.e., if there is a scheme of establishing correspondence 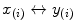between observations 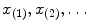of X and 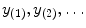of Y. In our example, the correspondence is defined by the two measurements being simultaneously performed on a given pair of entangled particles. Each such a pair of measurements corresponds to a certain input value, e.g., A 21 and B 21 correspond to 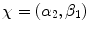. Therefore, no measurement outputs corresponding to different input values, such as A i1 and A i2, or A i1 and B i2 co-occur in the same sense in which, say, A i1 co-occurs with B i1.Related posts:
Integrated Neuropsychiatric Assessment System: A Generic Platform for Cognitive Neurodynamics Research
Dynamic Temporal-Topological Structure of Brain Network Within ADHD
Activity Patterns in Cortical Dynamics and the Illusion of Localized Representations
on the Neural Energy Coding
Cortical Singularities During the Cognitive Cycle Using Random Graph Theory
Electrodiffusive Formalism for Ion Concentration Dynamics in Excitable Cells and the Extracellular Space Surrounding Them
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
