(1)
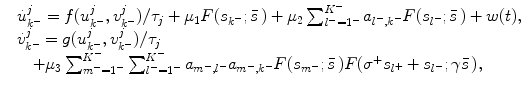
(2)
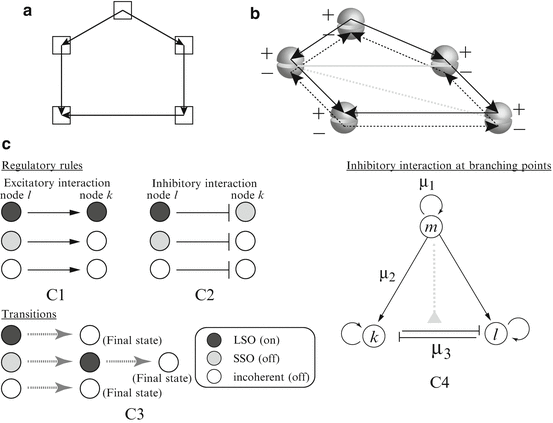
Fig. 1
(a) A graph whose vertices (squares) are connected by unidirectional edges (arrows). (b) Network structure corresponding to graph (a). The black solid and dashed arrows indicate excitatory links corresponding to systems (1) and (2), respectively. The gray solid and dashed lines indicate inhibitory links, which are added due to (C4). (c) (C1)(C2) Regulatory rules for excitatory and inhibitory interactions. (C3) Transient behavior when a node receives no input. The solution converges to an incoherent state for any initial condition. (C4) Bidirectional inhibitory interactions take place at the branching point. The activity of the inhibitory interactions is also controlled by s m (dashed line)
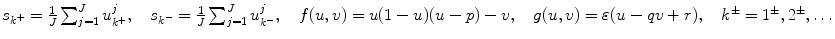 Here, t is dimensionless time, a dot above a variable indicates a derivative of the variable with respect to t, and μ i (i = 1, 2, 3) are positive constants. The node number k ± is responsible for the k-th vertex in the graph. A node consists of a group of oscillators. J and K + (or K −) correspond to the number of elements belonging to each node and the number of nodes, respectively. We set J = 15. The state of each node k ± is determined by the average of the amplitudes of the oscillators
Here, t is dimensionless time, a dot above a variable indicates a derivative of the variable with respect to t, and μ i (i = 1, 2, 3) are positive constants. The node number k ± is responsible for the k-th vertex in the graph. A node consists of a group of oscillators. J and K + (or K −) correspond to the number of elements belonging to each node and the number of nodes, respectively. We set J = 15. The state of each node k ± is determined by the average of the amplitudes of the oscillators 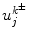 in the corresponding node, for example,
in the corresponding node, for example, 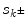 . We assume that the interaction function F has a threshold for activation. Regulation of on–off switching of the connecting nodes depends on s k , and is simply defined by the Heaviside function with a threshold
. We assume that the interaction function F has a threshold for activation. Regulation of on–off switching of the connecting nodes depends on s k , and is simply defined by the Heaviside function with a threshold 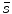 , where
, where 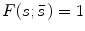 for
for 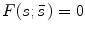 for
for 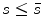 . The interactions affect all oscillators uniformly; that is, they are independent of j. Excitatory interaction directed from node l toward node k is expressed as a l, k , where a l, k = 1 and a l, k = 0 indicate the presence and absence of such interaction, respectively. We take
. The interactions affect all oscillators uniformly; that is, they are independent of j. Excitatory interaction directed from node l toward node k is expressed as a l, k , where a l, k = 1 and a l, k = 0 indicate the presence and absence of such interaction, respectively. We take 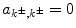 for all k ±.
for all k ±.The systems (1) and (2) are decoupled by taking 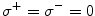 . The former and latter systems have forward and opposite directional excitatory links. That is, if a link from
. The former and latter systems have forward and opposite directional excitatory links. That is, if a link from 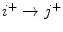 exists for (1) (
exists for (1) (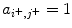 ), then a link from
), then a link from 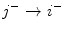 exists for (2) (
exists for (2) (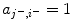 ). System (1) with
). System (1) with 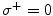 is the same as the system proposed in [10], and system (2) with
is the same as the system proposed in [10], and system (2) with 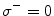 is the same as the previous system, except for the direction of the links. We refer to system (1) with
is the same as the previous system, except for the direction of the links. We refer to system (1) with 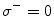 and system (2) with
and system (2) with 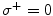 as system A and system B, respectively. We refer to the coupled system with
as system A and system B, respectively. We refer to the coupled system with 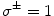 as system C.
as system C.
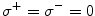 . The former and latter systems have forward and opposite directional excitatory links. That is, if a link from
. The former and latter systems have forward and opposite directional excitatory links. That is, if a link from 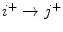 exists for (1) (
exists for (1) (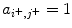 ), then a link from
), then a link from 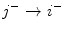 exists for (2) (
exists for (2) (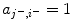 ). System (1) with
). System (1) with 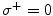 is the same as the system proposed in [10], and system (2) with
is the same as the system proposed in [10], and system (2) with 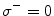 is the same as the previous system, except for the direction of the links. We refer to system (1) with
is the same as the previous system, except for the direction of the links. We refer to system (1) with 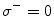 and system (2) with
and system (2) with 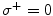 as system A and system B, respectively. We refer to the coupled system with
as system A and system B, respectively. We refer to the coupled system with 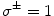 as system C.
as system C.The parameters p, q, r, and 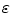 are independent of k ±, and set p = 0. 02, q = 1. 0,
are independent of k ±, and set p = 0. 02, q = 1. 0, 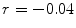 , and
, and 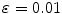 . Furthermore, w(t) is a small amount of random noise in the interval [0, 0. 05]. The time constants τ j take random values from the interval between τ − and τ +, where the values of τ − and τ + are set to
. Furthermore, w(t) is a small amount of random noise in the interval [0, 0. 05]. The time constants τ j take random values from the interval between τ − and τ +, where the values of τ − and τ + are set to 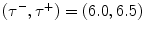 . The distribution of τ j is the same for all nodes; that is, it is independent of k.
. The distribution of τ j is the same for all nodes; that is, it is independent of k.
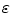 are independent of k ±, and set p = 0. 02, q = 1. 0,
are independent of k ±, and set p = 0. 02, q = 1. 0, 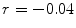 , and
, and 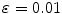 . Furthermore, w(t) is a small amount of random noise in the interval [0, 0. 05]. The time constants τ j take random values from the interval between τ − and τ +, where the values of τ − and τ + are set to
. Furthermore, w(t) is a small amount of random noise in the interval [0, 0. 05]. The time constants τ j take random values from the interval between τ − and τ +, where the values of τ − and τ + are set to 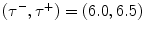 . The distribution of τ j is the same for all nodes; that is, it is independent of k.
. The distribution of τ j is the same for all nodes; that is, it is independent of k.Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree






