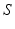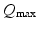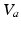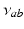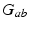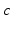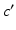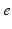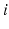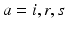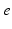Fig. 5.1
Schematic of “working brain” model, showing structures involved in corticothalamic generation of EEGs and the brainstem-hypothalamus ascending arousal system (see section “Arousal State Modeling” for abbreviations), with some of their main inputs, connections, and feedbacks shown by arrows. Adapted from Ref. [82]
Modeling
In this section we briefly review the key corticothalamic and arousal-system sectors of our model, parameter calibration, and links between the two sectors. More detailed discussion and further generalizations can be found elsewhere [63, 64, 68, 70, 72]. We note that other variants of most individual aspects of the model exist in the literature, but that detailed discussion of these variants is beyond the scope of the present chapter, where our aim is to unite the sectors as shown in Fig. 5.1.
General Neural-Field Modeling
The brain contains multiple populations of neurons, which we distinguish by a subscript 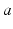 that designates both the structure in which a given population lies (e.g., a particular nucleus) and the type of neuron (e.g., interneuron, pyramidal cell). We average their properties over scales of ~ 0.1 mm and seek equations for the resulting mean-field quantities.
that designates both the structure in which a given population lies (e.g., a particular nucleus) and the type of neuron (e.g., interneuron, pyramidal cell). We average their properties over scales of ~ 0.1 mm and seek equations for the resulting mean-field quantities.
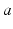 that designates both the structure in which a given population lies (e.g., a particular nucleus) and the type of neuron (e.g., interneuron, pyramidal cell). We average their properties over scales of ~ 0.1 mm and seek equations for the resulting mean-field quantities.
that designates both the structure in which a given population lies (e.g., a particular nucleus) and the type of neuron (e.g., interneuron, pyramidal cell). We average their properties over scales of ~ 0.1 mm and seek equations for the resulting mean-field quantities.The mean soma potential 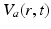 (measured relative to rest here) is approximated as the sum of contributions
(measured relative to rest here) is approximated as the sum of contributions 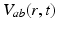 arriving as a result of activity at each type of (mainly) dendritic synapse
arriving as a result of activity at each type of (mainly) dendritic synapse  , where
, where  denotes both the population and neurotransmitter type,
denotes both the population and neurotransmitter type, 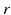 is the spatial coordinate, and
is the spatial coordinate, and 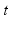 the time. This gives
the time. This gives
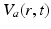 (measured relative to rest here) is approximated as the sum of contributions
(measured relative to rest here) is approximated as the sum of contributions 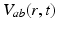 arriving as a result of activity at each type of (mainly) dendritic synapse
arriving as a result of activity at each type of (mainly) dendritic synapse 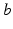 , where
, where 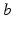 denotes both the population and neurotransmitter type,
denotes both the population and neurotransmitter type, 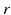 is the spatial coordinate, and
is the spatial coordinate, and 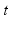 the time. This gives
the time. This gives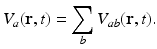
(5.1)
The potential 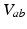 is generated when synaptic inputs from afferent neurons
is generated when synaptic inputs from afferent neurons 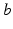 are temporally low-pass filtered and smeared out in time as a result of receptor dynamics and passage through the dendrites of neurons
are temporally low-pass filtered and smeared out in time as a result of receptor dynamics and passage through the dendrites of neurons 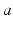 (i.e., by dynamics of ion channels, membranes, etc.). It approximately obeys the differential equation [69, 79, 72, 75]
(i.e., by dynamics of ion channels, membranes, etc.). It approximately obeys the differential equation [69, 79, 72, 75]
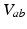 is generated when synaptic inputs from afferent neurons
is generated when synaptic inputs from afferent neurons 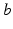 are temporally low-pass filtered and smeared out in time as a result of receptor dynamics and passage through the dendrites of neurons
are temporally low-pass filtered and smeared out in time as a result of receptor dynamics and passage through the dendrites of neurons 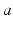 (i.e., by dynamics of ion channels, membranes, etc.). It approximately obeys the differential equation [69, 79, 72, 75]
(i.e., by dynamics of ion channels, membranes, etc.). It approximately obeys the differential equation [69, 79, 72, 75]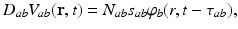
(5.2)
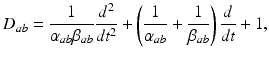
(5.3)
where 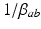 and
and 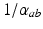 are the characteristic rise and decay times of the potential change due to an impulse at a dendritic synapse. The right of Eq. (5.2) describes the influence of the firing rates
are the characteristic rise and decay times of the potential change due to an impulse at a dendritic synapse. The right of Eq. (5.2) describes the influence of the firing rates  from neuronal populations
from neuronal populations 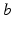 , in general delayed by a time
, in general delayed by a time 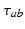 due to discrete anatomical separations between different structures. The quantity
due to discrete anatomical separations between different structures. The quantity 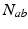 is the mean number of synapses to neurons of type
is the mean number of synapses to neurons of type 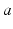 from type
from type 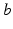 , and
, and 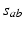 is the time-integrated response in neurons of type
is the time-integrated response in neurons of type 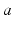 to a unit signal from neurons of type
to a unit signal from neurons of type 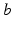 , implicitly weighted by the neurotransmitter release probability. In the present chapter we treat the
, implicitly weighted by the neurotransmitter release probability. In the present chapter we treat the 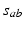 as constants and ignore their dynamics, which can be driven by neuromodulators, firing rate, and other effects; however, such dynamics can be incorporated straightforwardly [e.g., [13]].
as constants and ignore their dynamics, which can be driven by neuromodulators, firing rate, and other effects; however, such dynamics can be incorporated straightforwardly [e.g., [13]].
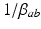 and
and 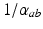 are the characteristic rise and decay times of the potential change due to an impulse at a dendritic synapse. The right of Eq. (5.2) describes the influence of the firing rates
are the characteristic rise and decay times of the potential change due to an impulse at a dendritic synapse. The right of Eq. (5.2) describes the influence of the firing rates 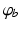 from neuronal populations
from neuronal populations 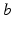 , in general delayed by a time
, in general delayed by a time 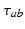 due to discrete anatomical separations between different structures. The quantity
due to discrete anatomical separations between different structures. The quantity 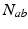 is the mean number of synapses to neurons of type
is the mean number of synapses to neurons of type 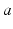 from type
from type 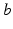 , and
, and 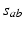 is the time-integrated response in neurons of type
is the time-integrated response in neurons of type 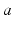 to a unit signal from neurons of type
to a unit signal from neurons of type 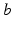 , implicitly weighted by the neurotransmitter release probability. In the present chapter we treat the
, implicitly weighted by the neurotransmitter release probability. In the present chapter we treat the 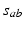 as constants and ignore their dynamics, which can be driven by neuromodulators, firing rate, and other effects; however, such dynamics can be incorporated straightforwardly [e.g., [13]].
as constants and ignore their dynamics, which can be driven by neuromodulators, firing rate, and other effects; however, such dynamics can be incorporated straightforwardly [e.g., [13]].Action potentials are produced at the axonal hillock when the soma potential 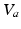 exceeds a threshold, at a rate that rises steeply with
exceeds a threshold, at a rate that rises steeply with 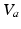 before leveling off. In a population, this dependence is smeared out by differences in individual neurons and their environments to yield the population-average response function
before leveling off. In a population, this dependence is smeared out by differences in individual neurons and their environments to yield the population-average response function
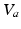 exceeds a threshold, at a rate that rises steeply with
exceeds a threshold, at a rate that rises steeply with 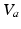 before leveling off. In a population, this dependence is smeared out by differences in individual neurons and their environments to yield the population-average response function
before leveling off. In a population, this dependence is smeared out by differences in individual neurons and their environments to yield the population-average response function![$$ {{Q}_{a}}(\mathbf{r},t)=S[{{V}_{a}}(\mathbf{r},t)], $$](/wp-content/uploads/2016/12/A319630_1_En_5_Chapter_Equ4.gif)
(5.4)
![$$ S[{{V}_{a}}(\mathbf{r},t)]=\frac{{{Q}_{\rm max}}}{1+{\rm exp}\{-[{{V}_{a}}(\mathbf{r},t)-{{\theta }_{a}}]/{\sigma }'\}}, $$](/wp-content/uploads/2016/12/A319630_1_En_5_Chapter_Equ5.gif)
(5.5)
where we assume a common mean neural firing threshold 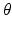 relative to resting, with
relative to resting, with 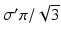 being its standard deviation (here,
being its standard deviation (here, 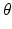 ,
, 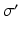 , and
, and 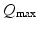 are assumed to be the same in all populations for simplicity). When treating linear perturbations relative to a given state, we make the approximation
are assumed to be the same in all populations for simplicity). When treating linear perturbations relative to a given state, we make the approximation
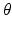 relative to resting, with
relative to resting, with 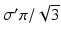 being its standard deviation (here,
being its standard deviation (here, 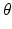 ,
, 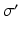 , and
, and 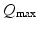 are assumed to be the same in all populations for simplicity). When treating linear perturbations relative to a given state, we make the approximation
are assumed to be the same in all populations for simplicity). When treating linear perturbations relative to a given state, we make the approximation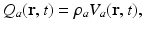
(5.6)
where 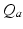 and
and 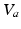 are now perturbations and
are now perturbations and 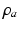 is the derivative of the sigmoid at an assumed steady state of the system in the absence of perturbations (we discuss the existence and stability of such states below).
is the derivative of the sigmoid at an assumed steady state of the system in the absence of perturbations (we discuss the existence and stability of such states below).
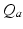 and
and 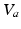 are now perturbations and
are now perturbations and 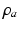 is the derivative of the sigmoid at an assumed steady state of the system in the absence of perturbations (we discuss the existence and stability of such states below).
is the derivative of the sigmoid at an assumed steady state of the system in the absence of perturbations (we discuss the existence and stability of such states below).Each neuronal population 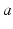 in the corticothalamic system produces a field
in the corticothalamic system produces a field 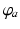 of pulses, that travels to other neuronal populations at a velocity
of pulses, that travels to other neuronal populations at a velocity 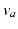 through axons with a characteristic range
through axons with a characteristic range 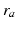 . This activity spreads out and dissipates if not regenerated. To a good approximation, this type of propagation obeys a damped wave equation [29, 44, 72]:
. This activity spreads out and dissipates if not regenerated. To a good approximation, this type of propagation obeys a damped wave equation [29, 44, 72]:
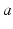 in the corticothalamic system produces a field
in the corticothalamic system produces a field 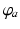 of pulses, that travels to other neuronal populations at a velocity
of pulses, that travels to other neuronal populations at a velocity 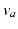 through axons with a characteristic range
through axons with a characteristic range 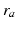 . This activity spreads out and dissipates if not regenerated. To a good approximation, this type of propagation obeys a damped wave equation [29, 44, 72]:
. This activity spreads out and dissipates if not regenerated. To a good approximation, this type of propagation obeys a damped wave equation [29, 44, 72]:![$$ {{D}_{a}}{{\varphi }_{a}}(\mathbf{r},t)=S[{{V}_{a}}(\mathbf{r},t)], $$](/wp-content/uploads/2016/12/A319630_1_En_5_Chapter_Equ7.gif)
(5.7)
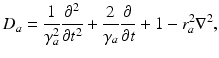
(5.8)
where the damping coefficient is 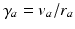 . Eqs. (5.7) and (5.8) yield propagation ranges in good agreement with anatomical results [10]. It is sometimes erroneously claimed that this propagation is an approximation to propagation with delta-function delays of the form
. Eqs. (5.7) and (5.8) yield propagation ranges in good agreement with anatomical results [10]. It is sometimes erroneously claimed that this propagation is an approximation to propagation with delta-function delays of the form 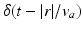 ; in reality, both mathematical approaches approximate the same physical system. More relevant is the fact that there is actually a range of velocities of propagation in axons [7, 30], which leads to a range of transit times for signals between any two points; however, this effect can be approximated via a corresponding increase in the effective synaptodendritic time constants (thereby spreading the response over a longer interval), which should then be interpreted as axo-synapto-dendritic quantities. More generally, a velocity spread can be introduced into the underlying propagator [8], or an appropriate generalized propagator could be derived.
; in reality, both mathematical approaches approximate the same physical system. More relevant is the fact that there is actually a range of velocities of propagation in axons [7, 30], which leads to a range of transit times for signals between any two points; however, this effect can be approximated via a corresponding increase in the effective synaptodendritic time constants (thereby spreading the response over a longer interval), which should then be interpreted as axo-synapto-dendritic quantities. More generally, a velocity spread can be introduced into the underlying propagator [8], or an appropriate generalized propagator could be derived.
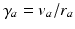 . Eqs. (5.7) and (5.8) yield propagation ranges in good agreement with anatomical results [10]. It is sometimes erroneously claimed that this propagation is an approximation to propagation with delta-function delays of the form
. Eqs. (5.7) and (5.8) yield propagation ranges in good agreement with anatomical results [10]. It is sometimes erroneously claimed that this propagation is an approximation to propagation with delta-function delays of the form 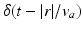 ; in reality, both mathematical approaches approximate the same physical system. More relevant is the fact that there is actually a range of velocities of propagation in axons [7, 30], which leads to a range of transit times for signals between any two points; however, this effect can be approximated via a corresponding increase in the effective synaptodendritic time constants (thereby spreading the response over a longer interval), which should then be interpreted as axo-synapto-dendritic quantities. More generally, a velocity spread can be introduced into the underlying propagator [8], or an appropriate generalized propagator could be derived.
; in reality, both mathematical approaches approximate the same physical system. More relevant is the fact that there is actually a range of velocities of propagation in axons [7, 30], which leads to a range of transit times for signals between any two points; however, this effect can be approximated via a corresponding increase in the effective synaptodendritic time constants (thereby spreading the response over a longer interval), which should then be interpreted as axo-synapto-dendritic quantities. More generally, a velocity spread can be introduced into the underlying propagator [8], or an appropriate generalized propagator could be derived.Equations (5.1)–(5.5), (5.7), and (5.8) form a closed nonlinear set, which can be solved numerically, or examined analytically in various limits. Once a set of specific neural populations has been chosen, and physiologically realistic values have been assigned to their parameters, these equations can be used to make predictions of neural activity. These equations govern spatiotemporal dynamics of firing rates; oscillations predicted from them are emergent changes of the average rate of spiking, whose frequencies do not usually equal the spiking frequency itself.
Corticothalamic System
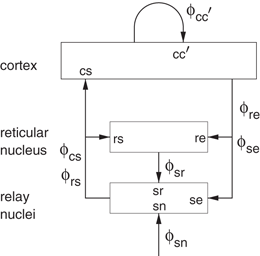
Much work has been done on applications of our neural field theory to the corticothalamic system, which is the first sector of the combined model of Fig. 5.1 to be discussed. This work has also included extensive verification and validation of the predictions against experiment, as discussed in the next section.
Figure 5.2 shows the large-scale structures and connectivities incorporated, including the thalamic reticular nucleus  , which inhibits relay (or specific) nuclei
, which inhibits relay (or specific) nuclei 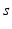 , and is lumped here with the perigeniculate nucleus, which has an analogous role [90, 94]. Relay nuclei convey external stimuli
, and is lumped here with the perigeniculate nucleus, which has an analogous role [90, 94]. Relay nuclei convey external stimuli 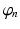 and pass on corticothalamic feedback. In this section we consider long-range excitatory cortical neurons
and pass on corticothalamic feedback. In this section we consider long-range excitatory cortical neurons  , short-range mainly inhibitory cortical neurons
, short-range mainly inhibitory cortical neurons  , neurons in the reticular nucleus
, neurons in the reticular nucleus 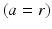 , neurons of thalamic relay nuclei
, neurons of thalamic relay nuclei 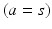 , and external inputs
, and external inputs 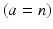 from non-corticothalamic neurons. These populations are discussed further below.
from non-corticothalamic neurons. These populations are discussed further below.
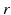 , which inhibits relay (or specific) nuclei
, which inhibits relay (or specific) nuclei 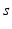 , and is lumped here with the perigeniculate nucleus, which has an analogous role [90, 94]. Relay nuclei convey external stimuli
, and is lumped here with the perigeniculate nucleus, which has an analogous role [90, 94]. Relay nuclei convey external stimuli 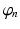 and pass on corticothalamic feedback. In this section we consider long-range excitatory cortical neurons
and pass on corticothalamic feedback. In this section we consider long-range excitatory cortical neurons 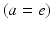 , short-range mainly inhibitory cortical neurons
, short-range mainly inhibitory cortical neurons 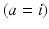 , neurons in the reticular nucleus
, neurons in the reticular nucleus 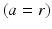 , neurons of thalamic relay nuclei
, neurons of thalamic relay nuclei 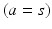 , and external inputs
, and external inputs 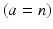 from non-corticothalamic neurons. These populations are discussed further below.
from non-corticothalamic neurons. These populations are discussed further below.If intracortical connectivities are proportional to the numbers of neurons involved—the random connectivity approximation—then 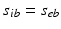 and
and 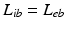 for each
for each 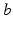 , whence
, whence 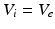 and
and 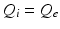 [73, 100]. This lets us concentrate on excitatory quantities, with inhibitory ones derivable from them (we stress that inhibitory effects are still included). The short range of
[73, 100]. This lets us concentrate on excitatory quantities, with inhibitory ones derivable from them (we stress that inhibitory effects are still included). The short range of 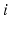 neurons and the small size of the thalamic nuclei enables us to assume
neurons and the small size of the thalamic nuclei enables us to assume 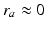 and, hence,
and, hence, 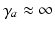 for
for 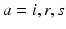 for many purposes. The only nonzero discrete delays are
for many purposes. The only nonzero discrete delays are 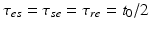 , where
, where 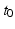 is the time for signals to pass from cortex to thalamus and back. We also assume that all the synaptodendritic time constants are equal, for simplicity, and set
is the time for signals to pass from cortex to thalamus and back. We also assume that all the synaptodendritic time constants are equal, for simplicity, and set 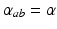 and
and 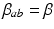 for all
for all 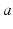 and
and 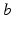 in what follows; this allows us to drop the subscripts
in what follows; this allows us to drop the subscripts 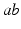 in Eqs. (5.2) and (5.3) and write
in Eqs. (5.2) and (5.3) and write 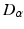 in place of
in place of 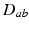 .
.
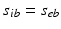 and
and 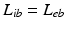 for each
for each 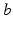 , whence
, whence 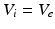 and
and 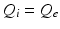 [73, 100]. This lets us concentrate on excitatory quantities, with inhibitory ones derivable from them (we stress that inhibitory effects are still included). The short range of
[73, 100]. This lets us concentrate on excitatory quantities, with inhibitory ones derivable from them (we stress that inhibitory effects are still included). The short range of 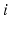 neurons and the small size of the thalamic nuclei enables us to assume
neurons and the small size of the thalamic nuclei enables us to assume 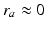 and, hence,
and, hence, 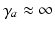 for
for 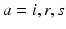 for many purposes. The only nonzero discrete delays are
for many purposes. The only nonzero discrete delays are 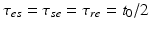 , where
, where 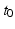 is the time for signals to pass from cortex to thalamus and back. We also assume that all the synaptodendritic time constants are equal, for simplicity, and set
is the time for signals to pass from cortex to thalamus and back. We also assume that all the synaptodendritic time constants are equal, for simplicity, and set 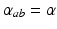 and
and 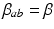 for all
for all 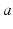 and
and 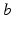 in what follows; this allows us to drop the subscripts
in what follows; this allows us to drop the subscripts 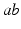 in Eqs. (5.2) and (5.3) and write
in Eqs. (5.2) and (5.3) and write 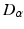 in place of
in place of 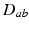 .
.Including only the connections shown in Fig. 5.2 and making the approximations mentioned above, our nonlinear model has 16 parameters, not all of which appear separately in the linear limit. By defining
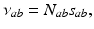
(5.9)
these are 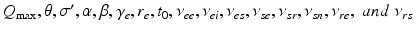 . These are sufficient to allow adequate representation of the most important anatomy and physiology, but few enough to yield useful interpretations and to enable reliable calibration of their values by fitting theoretical predictions to data. The parameters are approximately known from experiment [69, 70, 79, 75, 83] leading to the indicative values in Table 5.1. We use only values compatible with physiology. Sensitivities of the model to parameter variations have been explored in general [75] and in connection with variations between arousal states [76], as discussed below.
. These are sufficient to allow adequate representation of the most important anatomy and physiology, but few enough to yield useful interpretations and to enable reliable calibration of their values by fitting theoretical predictions to data. The parameters are approximately known from experiment [69, 70, 79, 75, 83] leading to the indicative values in Table 5.1. We use only values compatible with physiology. Sensitivities of the model to parameter variations have been explored in general [75] and in connection with variations between arousal states [76], as discussed below.
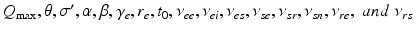 . These are sufficient to allow adequate representation of the most important anatomy and physiology, but few enough to yield useful interpretations and to enable reliable calibration of their values by fitting theoretical predictions to data. The parameters are approximately known from experiment [69, 70, 79, 75, 83] leading to the indicative values in Table 5.1. We use only values compatible with physiology. Sensitivities of the model to parameter variations have been explored in general [75] and in connection with variations between arousal states [76], as discussed below.
. These are sufficient to allow adequate representation of the most important anatomy and physiology, but few enough to yield useful interpretations and to enable reliable calibration of their values by fitting theoretical predictions to data. The parameters are approximately known from experiment [69, 70, 79, 75, 83] leading to the indicative values in Table 5.1. We use only values compatible with physiology. Sensitivities of the model to parameter variations have been explored in general [75] and in connection with variations between arousal states [76], as discussed below.Parameter | Description | Eyes-open | Spindle | Unit |
|---|---|---|---|---|
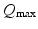 | Maximum firing rate | 340 | 340 | s−1 |
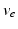 | Axonal velocity | 10 | 10 | ms−1 |
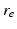 | Axonal range | 86 | 86 | mm |
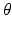 | Firing threshold | 12.9 | 12.9 | mV |
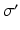 | Threshold spread | 3.8 | 3.8 | mV |
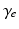 | Cortical damping rate | 116 | 116 | s−1 |
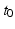 | Corticothalamic loop delay | 85 | 85 | ms |
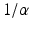 | Synaptodendritic decay time | 12 | 22 | ms |
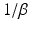 | Synaptodendritic rise time | 1.3 | 5.4 | ms |
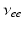 | Connection strength ( 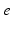 from from 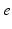 ) ) | 7.85 | 3.06 | mV s |
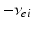 | Connection strength ( 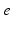 from from 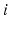 ) ) | 9.88 | 3.24 | mV s |
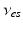 | Connection strength ( 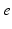 from from 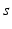 ) ) | 0.90 | 0.92 | mV s |
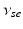 | Connection strength ( 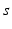 from from 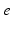 ) ) | 2.68 | 4.73 | mV s |
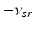 | Connection strength ( 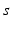 from from 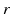 ) ) | 1.31 | 1.95 | mV s |
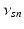 | Connection strength ( 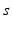 from from 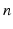 ) ) | 6.60 | 2.70 | mV s |
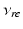 | Connection strength ( 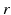 from from 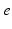 ) ) | 0.21 | 0.26 | mV s |
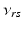 | Connection strength ( 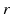 from from 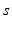 ) ) | 0.06 | 2.88 | mV s |
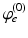 | Steady state firing rate ( 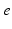 ) ) | 5.2 | 8.5 | s−1 |
 | Steady state firing rate ( 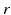 ) ) | 16.3 | 27.8 | s−1 |
 | Steady state firing rate ( 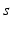 ) ) | 8.4 | 0.5 | s−1 |
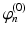 | Steady state firing rate ( 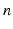 ) ) | 1 | 1 | s−1 |
An important implication of the parameters above is that the corticothalamic loop delay 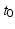 places any oscillations that involve this loop at frequencies of order 10 Hz. This means that inclusion of the thalamus and the dynamics of these loops is essential to understand phenomena at frequencies below ~20 Hz. At frequencies << 10 Hz it is sufficient to include a static corticothalamic feedback strength, and at frequencies >> 10 Hz the corticothalamic feedback is too slow and too attenuated by low-pass effects to influence the dynamics strongly.
places any oscillations that involve this loop at frequencies of order 10 Hz. This means that inclusion of the thalamus and the dynamics of these loops is essential to understand phenomena at frequencies below ~20 Hz. At frequencies << 10 Hz it is sufficient to include a static corticothalamic feedback strength, and at frequencies >> 10 Hz the corticothalamic feedback is too slow and too attenuated by low-pass effects to influence the dynamics strongly.
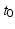 places any oscillations that involve this loop at frequencies of order 10 Hz. This means that inclusion of the thalamus and the dynamics of these loops is essential to understand phenomena at frequencies below ~20 Hz. At frequencies << 10 Hz it is sufficient to include a static corticothalamic feedback strength, and at frequencies >> 10 Hz the corticothalamic feedback is too slow and too attenuated by low-pass effects to influence the dynamics strongly.
places any oscillations that involve this loop at frequencies of order 10 Hz. This means that inclusion of the thalamus and the dynamics of these loops is essential to understand phenomena at frequencies below ~20 Hz. At frequencies << 10 Hz it is sufficient to include a static corticothalamic feedback strength, and at frequencies >> 10 Hz the corticothalamic feedback is too slow and too attenuated by low-pass effects to influence the dynamics strongly.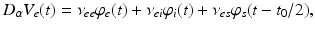
(5.10)
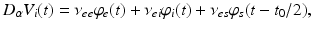
(5.11)
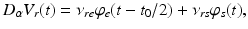
(5.12)
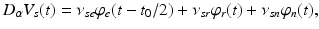
(5.13)
whence 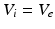 and
and 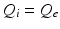 , as asserted above. The right side of each of Eqs (5.10)–(5.13) describes the spatial summation of all afferent activity (including via self-connections) for one neural population, and
, as asserted above. The right side of each of Eqs (5.10)–(5.13) describes the spatial summation of all afferent activity (including via self-connections) for one neural population, and 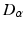 on the left describes temporal dynamics. The short ranges of the axons
on the left describes temporal dynamics. The short ranges of the axons 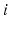 ,
, 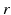 , and
, and 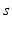 imply that the corresponding damping rates are large and that
imply that the corresponding damping rates are large and that 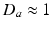 for these populations, further implying
for these populations, further implying
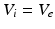 and
and 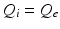 , as asserted above. The right side of each of Eqs (5.10)–(5.13) describes the spatial summation of all afferent activity (including via self-connections) for one neural population, and
, as asserted above. The right side of each of Eqs (5.10)–(5.13) describes the spatial summation of all afferent activity (including via self-connections) for one neural population, and 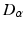 on the left describes temporal dynamics. The short ranges of the axons
on the left describes temporal dynamics. The short ranges of the axons 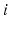 ,
, 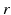 , and
, and 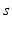 imply that the corresponding damping rates are large and that
imply that the corresponding damping rates are large and that 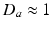 for these populations, further implying
for these populations, further implying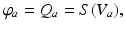
(5.14)
![$$ \left(\frac{1}{\gamma_{e}^{2}}\frac{{{\partial }^{2}}}{\partial {{t}^{2}}}+\frac{2}{{{\gamma }_{e}}}\frac{\partial }{\partial t}+1-r_{e}^{2}{{\nabla }^{2}}\right){{\varphi }_{e}}(\mathbf{r},t)=S[{{V}_{e}}(\mathbf{r},t)], $$](/wp-content/uploads/2016/12/A319630_1_En_5_Chapter_Equ15.gif)
(5.15)
with 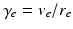 . Equations (5.10)–(5.15) describe our corticothalamic model. The neural mass limit correponds to
. Equations (5.10)–(5.15) describe our corticothalamic model. The neural mass limit correponds to 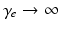 , when all delays within populations are negligible compared to the timescales of the phenomena of interest.
, when all delays within populations are negligible compared to the timescales of the phenomena of interest.
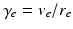 . Equations (5.10)–(5.15) describe our corticothalamic model. The neural mass limit correponds to
. Equations (5.10)–(5.15) describe our corticothalamic model. The neural mass limit correponds to 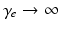 , when all delays within populations are negligible compared to the timescales of the phenomena of interest.
, when all delays within populations are negligible compared to the timescales of the phenomena of interest.Once neural activity has been predicted from stimuli, one must relate it to measurements to interpret experimental results. The limited spatiotemporal resolution of such measurements often provides an additional justification for the use of mean-field modeling, since finer structure is not resolvable. The quantity 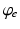 dominates in determining both EEG and fMRI signals—the former because of the dominance and highly aligned dipoles of pyramidal cells, the latter because of pyramidal cells’ predominance in cortical metabolic load. In both cases, it is the synaptic dynamics that predominate in determining the measured signals, so
dominates in determining both EEG and fMRI signals—the former because of the dominance and highly aligned dipoles of pyramidal cells, the latter because of pyramidal cells’ predominance in cortical metabolic load. In both cases, it is the synaptic dynamics that predominate in determining the measured signals, so 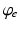 (not
(not 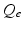 ) is the relevant variable. These points have been discussed in detail elsewhere [78, 71, 45, 74, 30].
) is the relevant variable. These points have been discussed in detail elsewhere [78, 71, 45, 74, 30].
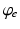 dominates in determining both EEG and fMRI signals—the former because of the dominance and highly aligned dipoles of pyramidal cells, the latter because of pyramidal cells’ predominance in cortical metabolic load. In both cases, it is the synaptic dynamics that predominate in determining the measured signals, so
dominates in determining both EEG and fMRI signals—the former because of the dominance and highly aligned dipoles of pyramidal cells, the latter because of pyramidal cells’ predominance in cortical metabolic load. In both cases, it is the synaptic dynamics that predominate in determining the measured signals, so 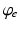 (not
(not 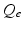 ) is the relevant variable. These points have been discussed in detail elsewhere [78, 71, 45, 74, 30].
) is the relevant variable. These points have been discussed in detail elsewhere [78, 71, 45, 74, 30].Arousal State Modeling
Transitions between wake and sleep states are primarily governed by the nuclei of the ascending arousal system (AAS) of the brainstem and hypothalamus, that project diffusely to the corticothalamic system, receive inputs from the suprachiasmatic nucleus (SCN) and elsewhere, and interact with sleep-promoting nuclei [86, 85]. A full description of sleep–wake transitions and their EEG correlates requires an integrated model of both the ascending arousal system and the corticothalamic system, including their mutual interactions. This section briefly describes how the nuclei of the AAS are modeled using the same methods as above [82].
The most important nuclei to model in the AAS are well established from physiology, and are shown in Fig. 5.1. These include the wake-promoting monoaminergic (MA) group and the sleep-promoting ventrolateral preoptic nucleus (VLPO), which inhibit one another, resulting in flip-flop dynamics if they interact strongly—only one is active at a time, and suppresses the other [84, 86, 85] to form the sleep-wake switch. In wake the MA is dominant, and in sleep the VLPO is dominant. State transitions are driven by inputs to the sleep-wake switch, including the circadian drive 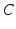 from the SCN and the homeostatic sleep drive
from the SCN and the homeostatic sleep drive 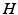 from buildup of metabolites (likely including adenosine, Ad, related compounds, or their byproducts) in wake and their clearance in sleep [55, 38, 101]. Cholinergic (ACh) and orexinergic (Orx, not shown in Fig. 5.1) inputs to the MA group are also present [48, 86, 85].
from buildup of metabolites (likely including adenosine, Ad, related compounds, or their byproducts) in wake and their clearance in sleep [55, 38, 101]. Cholinergic (ACh) and orexinergic (Orx, not shown in Fig. 5.1) inputs to the MA group are also present [48, 86, 85].
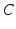 from the SCN and the homeostatic sleep drive
from the SCN and the homeostatic sleep drive 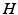 from buildup of metabolites (likely including adenosine, Ad, related compounds, or their byproducts) in wake and their clearance in sleep [55, 38, 101]. Cholinergic (ACh) and orexinergic (Orx, not shown in Fig. 5.1) inputs to the MA group are also present [48, 86, 85].
from buildup of metabolites (likely including adenosine, Ad, related compounds, or their byproducts) in wake and their clearance in sleep [55, 38, 101]. Cholinergic (ACh) and orexinergic (Orx, not shown in Fig. 5.1) inputs to the MA group are also present [48, 86, 85].Most models of human sleep have been either nonmathematical (e.g., based on sleep diaries) or abstract (mathematical, but not derived directly from physiology). The widely known two-process model is of the latter form, and includes circadian and homeostatic influences [15, 3]. Recent advances in sleep neurophysiology have enabled development of physiologically based models [51, 97, 16, 56, 62, 9]; here we use neural mass theory (NMT) to model the dynamics of the AAS nuclei.
Phillips and Robinson [51] argued that (i) since the system spends little time in transitions, the generation rate of 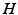 can be approximated as having two values, one for wake and one for sleep, (ii) the clearance rate of
can be approximated as having two values, one for wake and one for sleep, (ii) the clearance rate of 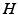 is assumed to be proportional to
is assumed to be proportional to 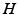 with a characteristic time scale
with a characteristic time scale 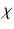 , and (iii) the production rate of
, and (iii) the production rate of 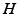 is
is 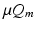 , where
, where 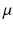 is a constant and
is a constant and 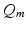 serves as a proxy for arousal state. These steps yield equations for
serves as a proxy for arousal state. These steps yield equations for 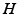 and the mean soma voltages
and the mean soma voltages 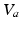 in the MA group (
in the MA group (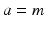 ) and VLPO (
) and VLPO (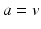 ):
):
 can be approximated as having two values, one for wake and one for sleep, (ii) the clearance rate of
can be approximated as having two values, one for wake and one for sleep, (ii) the clearance rate of  is assumed to be proportional to
is assumed to be proportional to 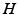 with a characteristic time scale
with a characteristic time scale 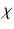 , and (iii) the production rate of
, and (iii) the production rate of 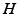 is
is 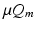 , where
, where 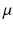 is a constant and
is a constant and 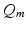 serves as a proxy for arousal state. These steps yield equations for
serves as a proxy for arousal state. These steps yield equations for 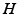 and the mean soma voltages
and the mean soma voltages 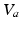 in the MA group (
in the MA group (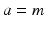 ) and VLPO (
) and VLPO (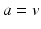 ):
):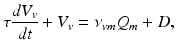
(5.16)
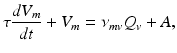
(5.17)
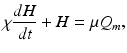
(5.18)
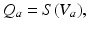
(5.19)
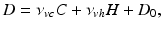
(5.20)
where the time constants 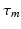 and
and 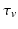 of the responses have been assumed equal to a common value
of the responses have been assumed equal to a common value 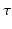 [these replace
[these replace 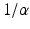 in Eq. (5.3), with
in Eq. (5.3), with 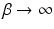 formally],
formally], 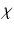 is the somnogen clearance time,
is the somnogen clearance time, 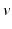 denotes VLPO,
denotes VLPO, 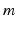 denotes MA, the
denotes MA, the 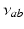 ,
, 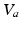 , and
, and 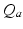 have the same meanings as in previous sections,
have the same meanings as in previous sections, 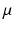 gives the proportionality between monoaminergic activity and somnogen generation rate.
gives the proportionality between monoaminergic activity and somnogen generation rate.
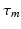 and
and 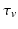 of the responses have been assumed equal to a common value
of the responses have been assumed equal to a common value 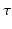 [these replace
[these replace 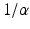 in Eq. (5.3), with
in Eq. (5.3), with 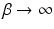 formally],
formally], 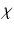 is the somnogen clearance time,
is the somnogen clearance time, 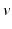 denotes VLPO,
denotes VLPO, 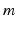 denotes MA, the
denotes MA, the 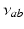 ,
, 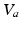 , and
, and 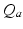 have the same meanings as in previous sections,
have the same meanings as in previous sections, 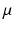 gives the proportionality between monoaminergic activity and somnogen generation rate.
gives the proportionality between monoaminergic activity and somnogen generation rate.The total sleep drive 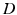 to the VLPO comprises
to the VLPO comprises 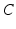 and
and 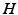 , where
, where 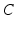 can be interpreted as the SCN firing rate and
can be interpreted as the SCN firing rate and 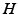 is a firing rate change due to somnogenic effects; in both cases only the terms
is a firing rate change due to somnogenic effects; in both cases only the terms 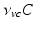 and
and 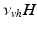 influence
influence 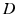 . The
. The 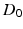 is a constant baseline level for the total sleep drive. When circadian entrainment to the natural light-dark cycle can be assumed, one has
is a constant baseline level for the total sleep drive. When circadian entrainment to the natural light-dark cycle can be assumed, one has
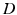 to the VLPO comprises
to the VLPO comprises 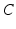 and
and 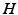 , where
, where 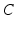 can be interpreted as the SCN firing rate and
can be interpreted as the SCN firing rate and 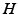 is a firing rate change due to somnogenic effects; in both cases only the terms
is a firing rate change due to somnogenic effects; in both cases only the terms 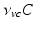 and
and 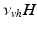 influence
influence 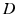 . The
. The 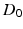 is a constant baseline level for the total sleep drive. When circadian entrainment to the natural light-dark cycle can be assumed, one has
is a constant baseline level for the total sleep drive. When circadian entrainment to the natural light-dark cycle can be assumed, one has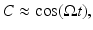
(5.21)
where 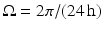 is the angular rate of Earth’s rotation, and the amplitude of
is the angular rate of Earth’s rotation, and the amplitude of 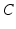 is absorbed into
is absorbed into 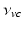 .
.
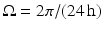 is the angular rate of Earth’s rotation, and the amplitude of
is the angular rate of Earth’s rotation, and the amplitude of 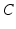 is absorbed into
is absorbed into 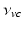 .
.In other cases, such as jetlag and shiftwork, 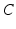 is modeled using the human circadian pacemaker model of St Hilaire et al. [96], which is the most recent version of the well-known model of the human circadian oscillator by Kronauer et al. [34]. The model includes (i) a light processing component, (ii) a component for the effects of non-photic stimuli, and (iii) a van der Pol oscillator component.
is modeled using the human circadian pacemaker model of St Hilaire et al. [96], which is the most recent version of the well-known model of the human circadian oscillator by Kronauer et al. [34]. The model includes (i) a light processing component, (ii) a component for the effects of non-photic stimuli, and (iii) a van der Pol oscillator component.
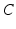 is modeled using the human circadian pacemaker model of St Hilaire et al. [96], which is the most recent version of the well-known model of the human circadian oscillator by Kronauer et al. [34]. The model includes (i) a light processing component, (ii) a component for the effects of non-photic stimuli, and (iii) a van der Pol oscillator component.
is modeled using the human circadian pacemaker model of St Hilaire et al. [96], which is the most recent version of the well-known model of the human circadian oscillator by Kronauer et al. [34]. The model includes (i) a light processing component, (ii) a component for the effects of non-photic stimuli, and (iii) a van der Pol oscillator component.In light processing, retinal photoreceptors are converted from ready to activated state by photons at a rate 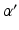 , dependent on light intensity
, dependent on light intensity 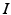 :
:
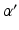 , dependent on light intensity
, dependent on light intensity 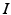 :
: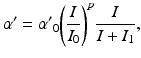
(5.22)
where 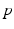 ,
, 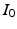 , and
, and 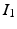 are constants used to adjust the model dynamics to experimental data. Activated photoreceptors are converted back to ready at a constant rate
are constants used to adjust the model dynamics to experimental data. Activated photoreceptors are converted back to ready at a constant rate 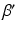 . Thus the fraction
. Thus the fraction 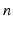 of activated photoreceptors follows
of activated photoreceptors follows
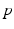 ,
, 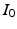 , and
, and 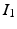 are constants used to adjust the model dynamics to experimental data. Activated photoreceptors are converted back to ready at a constant rate
are constants used to adjust the model dynamics to experimental data. Activated photoreceptors are converted back to ready at a constant rate 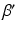 . Thus the fraction
. Thus the fraction 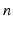 of activated photoreceptors follows
of activated photoreceptors follows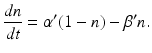
(5.23)
The resultant photic drive 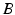 is proportional to the rate
is proportional to the rate 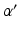 and the fraction of photoreceptors that can be activated
and the fraction of photoreceptors that can be activated 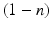 :
:
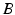 is proportional to the rate
is proportional to the rate 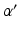 and the fraction of photoreceptors that can be activated
and the fraction of photoreceptors that can be activated 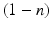 :
: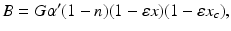
(5.24)
where 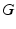 and
and 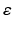 are constants adjusted to fit experimental data [96], and
are constants adjusted to fit experimental data [96], and 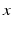 and
and 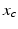 are the circadian variables of the oscillator. The term
are the circadian variables of the oscillator. The term 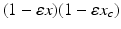 accounts for the experimentally observed phase-dependent sensitivity of the circadian pacemaker to light.
accounts for the experimentally observed phase-dependent sensitivity of the circadian pacemaker to light.
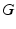 and
and 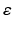 are constants adjusted to fit experimental data [96], and
are constants adjusted to fit experimental data [96], and 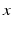 and
and 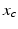 are the circadian variables of the oscillator. The term
are the circadian variables of the oscillator. The term 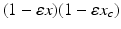 accounts for the experimentally observed phase-dependent sensitivity of the circadian pacemaker to light.
accounts for the experimentally observed phase-dependent sensitivity of the circadian pacemaker to light.The non-photic effects, such as meals and locomotion, on the circadian oscillator are modeled as increased stimulation during wake hours:
![$$ {{N}_{s}}=\rho \left(\frac{1}{3}-s \right)[1-\text{t}{\rm anh}(10x) ], $$](/wp-content/uploads/2016/12/A319630_1_En_5_Chapter_Equ25.gif)
(5.25)
where 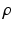 is a constant reflecting strength of the non-photic stimulation, and
is a constant reflecting strength of the non-photic stimulation, and 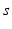 equals 1 during wakefulness and 0 during sleep, providing for state-dependency. The factor in the square brackets accounts for stronger nonphotic effects near the minimum of core body temperature [96].
equals 1 during wakefulness and 0 during sleep, providing for state-dependency. The factor in the square brackets accounts for stronger nonphotic effects near the minimum of core body temperature [96].
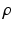 is a constant reflecting strength of the non-photic stimulation, and
is a constant reflecting strength of the non-photic stimulation, and 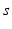 equals 1 during wakefulness and 0 during sleep, providing for state-dependency. The factor in the square brackets accounts for stronger nonphotic effects near the minimum of core body temperature [96].
equals 1 during wakefulness and 0 during sleep, providing for state-dependency. The factor in the square brackets accounts for stronger nonphotic effects near the minimum of core body temperature [96].The circadian oscillator thus follows
![$$ \frac{dx}{dt}=\Omega \left[{{x}_{c}}+\gamma \left(\frac{1}{3}x+\frac{4}{3}{{x}^{3}}-\frac{256}{105}{{x}^{7}}\right)+B+{{N}_{s}}\right], $$](/wp-content/uploads/2016/12/A319630_1_En_5_Chapter_Equ26.gif)
(5.26)
![$$ \frac{d{{x}_{c}}}{dt}=\Omega \left[qB{{x}_{c}}-x\left\{{{\left(\frac{\delta }{{{\tau }_{c}}}\right)}^{2}}+kB \right\} \right], $$](/wp-content/uploads/2016/12/A319630_1_En_5_Chapter_Equ27.gif)
(5.27)
where 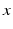 is the pacemaker activity,
is the pacemaker activity, 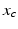 is a complementary variable,
is a complementary variable, 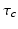 is an intrinsic circadian period,
is an intrinsic circadian period, 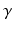 is the stiffness of the oscillator,
is the stiffness of the oscillator, 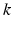 and
and 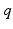 determine strength of the photic drive
determine strength of the photic drive 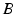 ,
, 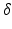 is a correction factor that ensures the correct intrinsic circadian period, and
is a correction factor that ensures the correct intrinsic circadian period, and 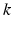 is positive for diurnal animals [34, 28]. The numerical coefficients in Eqs. (5.26) and (5.27) were chosen to achieve unit amplitude of the limit cycle.
is positive for diurnal animals [34, 28]. The numerical coefficients in Eqs. (5.26) and (5.27) were chosen to achieve unit amplitude of the limit cycle.
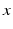 is the pacemaker activity,
is the pacemaker activity, 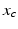 is a complementary variable,
is a complementary variable, 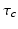 is an intrinsic circadian period,
is an intrinsic circadian period, 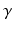 is the stiffness of the oscillator,
is the stiffness of the oscillator, 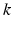 and
and 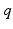 determine strength of the photic drive
determine strength of the photic drive 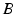 ,
, 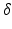 is a correction factor that ensures the correct intrinsic circadian period, and
is a correction factor that ensures the correct intrinsic circadian period, and 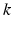 is positive for diurnal animals [34, 28]. The numerical coefficients in Eqs. (5.26) and (5.27) were chosen to achieve unit amplitude of the limit cycle.
is positive for diurnal animals [34, 28]. The numerical coefficients in Eqs. (5.26) and (5.27) were chosen to achieve unit amplitude of the limit cycle.Core body temperature (CBT) demonstrates circadian fluctuations and timing of CBT minimum is often used as a marker of circadian phase. In entrained individuals it typically appears about 2 h before awakening, and is calculated as:
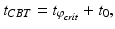
(5.28)
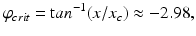
(5.29)
where 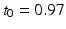 h is a constant and
h is a constant and 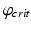 is a phase difference between the circadian variables
is a phase difference between the circadian variables 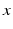 and
and 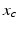 given in radians.
given in radians.
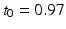 h is a constant and
h is a constant and 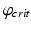 is a phase difference between the circadian variables
is a phase difference between the circadian variables 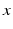 and
and 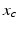 given in radians.
given in radians.Connections between the AAS and the circadian oscillator systems are reciprocal: (i) the circadian variable  has an effect on the VLPO, as described in Eq. (5.20), and (ii) the AAS system has an effect on
has an effect on the VLPO, as described in Eq. (5.20), and (ii) the AAS system has an effect on 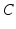 by reducing (or setting to zero lux) the light input
by reducing (or setting to zero lux) the light input 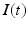 during sleep.
during sleep.
 has an effect on the VLPO, as described in Eq. (5.20), and (ii) the AAS system has an effect on
has an effect on the VLPO, as described in Eq. (5.20), and (ii) the AAS system has an effect on 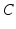 by reducing (or setting to zero lux) the light input
by reducing (or setting to zero lux) the light input 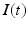 during sleep.
during sleep.The parameters in the above model have the nominal values in Table 5.2, determined by physiological constraints from the literature and comparison with a restricted set of experiments on normal sleep, sleep deprivation, and the effects of light on circadian phase [51, 52, 96, 34, 28]. The theory then predicts phenomena in regimes outside those of the calibration experiments, with only slight adjustments to account for individual state and trait differences—these adjustments can be compared with what is expected from independent physiological analyses; e.g., a long circadian period 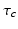 should be associated with the evening (“night owl”) chronotype, while short
should be associated with the evening (“night owl”) chronotype, while short 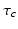 should be associated with morning type [54].
should be associated with morning type [54].
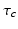 should be associated with the evening (“night owl”) chronotype, while short
should be associated with the evening (“night owl”) chronotype, while short 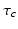 should be associated with morning type [54].
should be associated with morning type [54].Table 5.2
Parameter values of the AAS model and their units. The sigmoid parameters carry an extra prime to indicate that they can differ from the cortical values in Table 5.1
AAS | Circadian pacemaker | ||||
|---|---|---|---|---|---|
Quantity | Nominal | Unit | Quantity | Nominal | Unit |
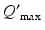 | 100 | s−1 | 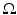 | 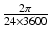 | s−1 |
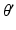 | 10 | mV | 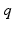 | 1/3 | – |
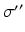 | 3 | mV | 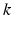 | 0.55 | – |
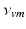 | − 2.1 | mV s | 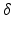 | 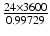 | s |
 Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
 Get Clinical Tree app for offline access
Get Clinical Tree app for offline access

| |||||