accumulation. This can help elucidate a mechanism of age-dependent theta oscillation changes in AD mouse models, reflecting changes in synchronous synaptic activity that could mediate oscillation-dependent memory deficiencies and serve as a biomarker for amyloid-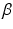 accumulation.
accumulation.
Key words:
Quantitative systems pharmacologyNeural oscillationDynamical diseasesTheta rhythmAnxietyAlzheimer’s diseaseDynamic and Computational Neuropharmacology (Quantitative and Systems Pharmacology)
The Partially Admitted Renaissance of Systems Theory and of Cybernetics
Systems Theory and Cybernetics
Systems theory was proposed by Ludwig von Bertalanffy (1901–1972), a biologist who worked on the basic principles of life and searched for universal laws of organization [80]. The basic concepts of the systems approach are: (i) a system is a whole that functions by virtue of the interaction of its parts, and (ii) is defined by its elements and the relationship among these elements; (iii) the systems approach integrates the analytic and synthetic methods by taking into account the interaction of the system with its environment; (iv) living structures are open systems, which interact with other systems outside of themselves. Bertalanffy’s conceptual model of the living organism as an open system has had revolutionary implications for life and behavioral sciences.
Cybernetics, as a scientific discipline has been named by Norbert Wiener (1894–1964). It was the title of his book with the subtitle Control and Communication in the Animal and the Machine [86]. Cybernetics was a pluralistic theory and an interdisciplinary movement of a number of leading intellectuals. The term cybernetics goes back to Plato, when he explained the principles of political self-governance. goal-directed behavior
Wiener himself emphasized the role of feedback mechanisms in the goal-oriented systems. While the physiologists already knew that the involuntary (autonomous) nervous systems control Bernard’s internal milieu, he extended the concept suggesting that the voluntary nervous system may control the environment by some feedback mechanisms and searched for a theory of goal-oriented behavior. This theory supplemented with the concept of circular causality promised a new framework to understand the behavior of animals, humans, and computers just under design and construction that time.
The other supporting pillar of cybernetics is the brain-computer analogy suggested by the spirit of the McCulloch-Pitts Neuron (MCP neuron). An MCP [55] neuron is a formal model, and it can be identified as a binary threshold unit. A neuron initiates an impulse if the weighted sum of their inputs exceeds a threshold, otherwise it remains in silence.The MCP model framework wanted to capture the logical basis of neural computation, and intentionally contains neurobiological simplifications. The state is binary, the time is discrete, the threshold and the wiring are fixed. Chemical and electrical interactions are neglected, glial cells are also not taken into consideration. McCulloch and Pitts showed that a large enough number of synchronously updated neurons connected by appropriate weights could perform many possible computations. From retrospective we see that bottom up models of brain regions can be built based on networks of interconnected single cell models.
McCulloch (1898–1969) served as the chairman of a series of conferences (Macy conferences held between 1946–1953 sponsored by and named after the Macy Foundation, where at the beginning Wiener also played an important role. The main topics of the conferences were: (i) Applicability of a Logic Machine Model to both Brain and Computer, (ii) Analogies between Organisms and Machines; (iii) Information Theory; (iv) Neuroses and Pathology of Mental Life and (v) Human and Social Communication.
Systems theory and cybernetics emphasized the importance of organization principles and the have anticipated the use of abstract computational models in biology to study normal and pathological phenomena.
Genetic Determinism, Biological Complexity and Systems Biology
It is a mere coincidence that the last Macy conference was held in the same year (1953) when the Watson–Crick [11] paper was published. The research program of the new “molecular biology” suggested that the replication, transcription and translation of the genetic material should and could be explained by chemical mechanisms. Crick’s central dogma of molecular biology stated that there was a unidirectional information flow from DNA via RNA (ribonucleic acid) to proteins.
While the central dogma was enormously successful in discovering many detailed chemical processes of life phenomena, philosophically it suggested, as Crick himself wrote [10], that “the ultimate aim of the modern movement in biology is to explain all biology in terms of physics and chemistry”.1
The central dogma led to genetic determinism. While certain phenotypes can be mapped to a single gene, the extreme form of genetic determinism, which probably nobody believes, would state that all phenotypes are purely genetically determined. Genetic determinism has lost its attraction as a unique explanation for the appearance of specific phenotypic traits. After 60 years of extensive research in molecular biology, there is a very good understanding of the intricate mechanisms that allow genes to be translated into proteins. However, this knowledge has given us very little insight about the causal chains that link genes to the morphological and other phenotypic traits of organisms [48]. Also, human diseases due to genetic disorders are the results of the interaction of many gene products. One generally used method to understand the performance of a complex genetic networks is the transgenic techniques.
In the spirit of systems theory and of cybernetics Robert Rosen (1934–1998) [58, 59] gave a formalism, which connected phenotype (i.e. what we can observe directly about an organism) and genotype (the genetic makeup). In particular, phenotype is interpreted as being “caused” by genotype. He also argued that to understand biological phenotype, in addition to the Newtonian paradigm, the organizational principles should be uncovered. He realized that a crucial property of living systems, that while they are thermodynamically open systems, organizationally they should be closed. To put it in another way, all components, which are subject of degradation due to ordinary wear and tear, should be repaired or resynthesized within the cell. Rosen gave a mathematical framework to show how it is possible to do.
Systems biology is an emergent movement to combine system-level description with microscopic details. It might be interpreted as the renaissance of cybernetics and of system theory, materialized in the works of Robert Rosen. In an excellent review Olaf Wolkenhauer [87] explained how the concepts of systems theory, and of cybernetics were applied by Rosen to biology, and how his ideas returned now under the name of systems biology. For a very good new introductory textbook on systems biology, see [30].
Genetic reductionism, in particular, has been abandoned as a useful explanatory scheme for understanding the phenotypic traits of complex biological systems. Genes are increasingly studied today because they are involved in the genetic program that unfolds during development and embryogenesis rather than as agents responsible for the inheritance of traits from parents to offspring [73].
As a reaction to something that some people might have seen as the “tyranny of molecular biology”, the systems thinking has been revitalized in the last several years. Systems thinking correctly states that while reductionist research strategy was very successful, it underestimates the complexity of life. It is clear, that decomposing, dissecting and analyzing constituents of a complex system is indispensable and extremely important. Molecular biology achieved a lot to uncover the structures of many chemical molecules and chemical reactions among the molecules behind life processes. The typical molecular biologist’s approach suggests that there is an “upward causation” from molecular states to behavior. The complex systems perspective [15] does not deny the fundamental results of molecular biology, but emphasizes other principles of biological organization.
One of the pioneers of systems biology, Denis Noble offers ten principles of systems biology [52]:
1.
Biological functionality is multi-level
2.
Transmission of information is not one way
3.
DNA is not the sole transmitter of inheritance
4.
The theory of biological relativity: there is no privileged level of causality
5.
Gene ontology will fail without higher-level insight
6.
There is no genetic program
7.
There are no programs at any other level
8.
There are no programs in the brain
9.
The self is not an object
10.
There are many more to be discovered; a genuine “theory of biology” does not yet exist
Systems biology emphasizes (i) the interactions among cell constituents and (ii) the dynamic character of these interactions. Biological systems are paradigmatic of hierarchical dynamical systems. For such systems, levels are often connected by some feedback control mechanism. Famously, protein channels carry current that changes the membrane potential of a cell, while the membrane potential changes the protein channels. This mechanism implements circular causality.
Generally, what we see is that systems biology, partially unwittingly, returned to its predecessors, systems theory and cybernetics.
Systems Neuroscience and Systems Neuropharmacology
Systems Neuroscience is a field devoted to understanding whole systems of the brain, such as those involved in sensation, movement, learning and memory, attention, reward, decision-making, reasoning, executive functions, and emotions. The structural, functional and dynamic aspects are integrated into a coherent framework [3]. It also deals with the principles of information processing, storage and retrieval at the systems level.
The study of brain systems includes the analysis of individual regions, as well as hierarchical levels of information processing. In terms of methodologies, it benefits from diverse techniques from single-cell recording to high-resolution imaging of brain activity. Systems neuroscience also uses computational studies to organize data into a coherent picture.
While the standard structure-based design of drugs for psychiatric disorders is based on drug-receptor interactions, the systems physiology perspective [7] emphasizes the effects of drugs on spatiotemporal brain activities. The theoretical framework for understanding normal and pathological spatiotemporal activities should be dynamical system theory to identify targets, and then, in the next stage, chemists should design molecules to modify the desired target.
Dynamical system theory and computational neuroscience combined with traditional molecular and electrophysiological methods would open new avenues in drug discovery that may lead to genuinely new neurological and psychiatric therapies [1]. More specifically, these model-based highly valuable techniques are able to integrate multiple disciplines at different spatiotemporal scales [16].
Recently the concepts and methods of systems biology have been used in pharmacology [67] and psychiatry [70]. Specifically Noble [52] states that there is no privileged level of causality, and there is no reason to assume that the molecular/genetic level uniquely determines mental activities, so the levels should be integrated.
Our own belief is [72]: “…Multi-scale modeling has multiple meanings and goals including different time and spatial scales, levels of organization, even multi-stage processing. While the significance and importance of describing neural phenomena at different levels simultaneously is clear in many cases, we certainly don’t have a single general mathematical framework. Mostly we have specific examples for coupling two or more levels. The understanding and control of normal and pathological behavior, the transfer of knowledge about the brain function and dynamics to establish new computational and technological devices needs the integration of molecular, cellular, network, regional and system levels, and now the focus ins on elaborating mathematically well-founded and biologically significant multi-scale models.”
Quantitative Systems Pharmacology
The main goal of computational neuroscience is to build biologically realistic mathematical models, and test how they match and predict experimental research by using computer simulations. Its main mathematical tool is dynamical system theory which helps to understand the neural mechanisms of temporal and spatio-temporal neural activities.The discipline of computational neuropharmacology emerged [1] as pharmaco-therapeutic strategies were suggested by constructing biophysically realistic mathematical models of neurological and psychiatric disorders.
Nowadays the term “Quantitative Systems Pharmacology” QSP is used and defined as “…an approach to translational medicine that combines computational and experimental methods to elucidate, validate and apply new pharmacological concepts to the development and use of small molecule and biologic drugs. QSP will provide an integrated ‘systems- level’ approach to determining mechanisms of action of new and existing drugs in preclinical and animal models and in patients. QSP will create the knowledge needed to change complex cellular networks in a specified way with mono or combination therapy, alter the pathophysiology of disease so as to maximize therapeutic benefit and minimize toxicity and implement a ‘precision medicine’ approach to improving the health of individual patient.…”. As an NIH White Paper by the QSP Workshop Group writes [67]. “…The concept of QSP in CNS is tightly linked to the term of ‘computational neuropharmacology’, an area inspired by seminal work of the late Leif Finkel [19] and further developed as ‘computational neuropharmacology”’ [1, 21]. QSP promises to build network and circuit level models based on detailed models of single neurons and synaptic transmission bu using morphological, biophysical and cellular electrophysiological data. The effects of drugs acting on intrinsic neuron and synaptic parameters are directly incorporated into the model.
In this paper we adopt the approach of quantitative systems pharmacology to get a better understanding the effects and neural mechanisms of potential anxiolytic drugs on hippocampal theta oscillations and study the relationship between altered network connectivity and hippocampal pattern, which may be related to the eventual early diagnosis of Alzheimer’s disease.
Abnormal Neural Oscillation
Neural rhythmicity is known to be involved in cognition and motor behavior [7, 83] and pathological symptoms are related to altered temporal patterns. The understanding of the underlying cellular, synaptic and network level mechanisms of these altered patterns contribute to obtain more knowledge about the neural mechanisms of certain neurological and psychiatric diseases, and may help to the elaboration of more advanced therapeutic strategies. The iterative combination of experiments and computational studies was recently offered [9, 18, 60] to achieve this goal. Some relationship between disorders and altered temporal pattern will be very briefly mentioned here.
Epilepsy
A variety of temporal pattern is associated to different types of epileptic behaviors [43, 56] explained by the dynamical diseases paradigm. Both macroscopic, population level models championed by Lopes Da Silva [43] and biophysically detailed epilepsy models exist (famously reflected in the works of Roger Traub, say [69]). The prediction and control of epileptic seizures became a hot, and controversial topic: [49] has 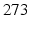 citations (
citations ( ).Dynamical models may predict seizure development and the administration of drugs could be designed accordingly providing novel therapeutic strategies for epileptic patients.
).Dynamical models may predict seizure development and the administration of drugs could be designed accordingly providing novel therapeutic strategies for epileptic patients.
 citations (
citations ( ).Dynamical models may predict seizure development and the administration of drugs could be designed accordingly providing novel therapeutic strategies for epileptic patients.
).Dynamical models may predict seizure development and the administration of drugs could be designed accordingly providing novel therapeutic strategies for epileptic patients.Abnormal Cortical Rhythms in Parkinson Disease
Abnormal synchronised oscillatory activities may contribute to bradykinesia in patients with Parkinson’s disease [4, 17, 57]. Neuronal correlates of PD include a shift to lower frequencies and enhanced synchronized oscillations at low theta (3–7 Hz) and beta 10–30 Hz regions in the basal ganglia, thalamus, and cortex.
Phase-amplitude coupling (PAC), a phenomenon that may emerge in spatially distributed oscillating network [33]. It describes the coupling between the phase of a slow oscillation and the amplitude of a fast oscillation, with the highest amplitude occurring at the so-called preferred coupling phase. It was suggested [12] that exaggerated PAC in the primary motor cortex is associated to PD. Pathological beta oscillation may have striatal origin, and combined physiological and computational models (e.g. [44]) contributed the uncover some details of the pathophysiological mechanism.
Abnormal neural oscillations and synchrony in schizophrenia
There are accumulating evidences that alterations in the synchronized neural oscillatory activity may have an important role in the pathophysiology of schizophrenia. Abnormal beta and gamma oscillations emerge due to the impaired synaptic transmission in the network GABAergic [71]. The “GABAergic origin hypothesis” [51] suggests that hypofunction of N-methyl-d-aspartic acid-type glutamate receptors (NMDARs) at GABAergic interneurons is sufficient for generating schizophrenia-like effects. Mostly parvalbumin containing interneurons are involved, as computational studies [79] also suggest. Not only high frequency oscillations, but low frequency rhythms including delta patterns may be related to the pathophysiology of schizophrenia [39, 47].
Just as oscillations can provide potentially useful temporal organization of processing within a region, so they can also support efficient inter-regional processing. It has been hypothesised that inter-region coherence may be a general mechanism for task-led inter-regional communication [20, 81]. Sigurdsson et al. (2010) investigated hippocampal-prefrontal coupling in a mouse model of schizophrenia. They contrasted the choice (test) runs vs. the sample runs in a discrete-trial, T-maze, working memory task. In wild-type mice, replicating the findings of Jones and Wilson (2005) in rats, they showed that both theta-band coherence of the two regions LFPs, and phase-locking of medial prefrontal neuronal firing to CA1 theta, was higher during choice runs. In the schizophrenia-model mice, however, this theta-band coupling was impaired.
Abnormal Brain Rhythms in ADHD
There are newer developments in the understanding of the of the normal and pathological mechanisms of attention related to the entrainment of internal neural oscillations to external rhythms [8, 42]. Phase-amplitude coupling plays also role as a mechanism of entrainment. Abnormal neural oscillations and selective attention deficits occur in Attention Deficit Hyperactivity Disorder (ADHD) and in other psychiatric disorders. Findings of abnormal entrainment may lead to new to therapeutic interventions.
Anxiolytic Drugs and Altered Hippocampal Theta Rhythms
Background
In the behaving mammal, hippocampal theta, a sinusoidal 4–12 Hz fluctuation in the hippocampal local field potential, is very prominent during behaviors which involve spatial translation of the head [53, 74] or arousal and anxiety [31, 62, 65]. Studies focusing on theta amplitude/power have long noted that hippocampal theta has an atropine-sensitive component and atropine-resistant component [41]. The general observation is that systemic injection of non-specific muscarinic antagonists such as atropine and scopolamine eliminate the theta (type II component) that is observed during alert immobility (aroused/anxious states,) and certain anaesthetised states, but fairly minimally affect the theta (type I component) observed during locomotion [6, 41]. Lesions to the septum eliminate both components of hippocampal theta. Hippocampal theta plays a key role in two functions associated with the hippocampus: (1) spatial cognition and memory; (2) anxiety and anxiolytic drug action. We focus on the latter here.
Figure 2.1 shows the empirical finding. Figure 2.1a shows that increasing the strength of the reticular stimulation increases the frequency of the theta oscillation, and that the relationship is broadly linear. Figure 2.1b shows the effects of various drugs upon this relationship. Only the anxiolytic drugs (chlordiazepoxide, diazepam, alprazolam, and amylobarbitone) reduce theta frequency, while the antipsychotic drugs (haloperidol, chlorpromazine) do not. Figure 2.1c shows the reduction of theta frequency by buspirone, a later-discovered anxiolytic acting at 5HT-1A receptors. As a group, anxiolytics reduce the slope and/or intercept of the relationship between stimulation strength and theta frequency.
To enhance the validity of the theta-frequency reduction assay and to provide a test bed for theta-behaviour relationships, it is important to extend the assay to the freely behaving animal. Accordingly, we recently tested two well-established anxiolytic drugs (chlordiazepoxide, a benzodiazepine, and buspirone, a 5HT-1A agonist) and a putative anxiolytic drug (O-2545, a CB1 agonist) in the awake and locomoting rat in a foraging task. Figure 2.1d, e, f shows the results. Notably, there is a broadly linear relationship between theta frequency and running speed. Interestingly, all three anxiolytic drugs elicited a specific form of theta frequency reduction; they reduced the intercept of this relationship, as measured by the intercept of the frequency-speed regression at 0 cm/s. The specificity of this anxiolytic-elicited effect is suggested by the contrast to the reduction of the slope of the frequency-speed regression (Fig. 2.1g) elicited by introducing the rats to a new spatial context (a dissociation and effect predicted by a theta oscillatory interference model of grid cells and place cells (see [5] and [85] for more details)).
The approach of quantitative systems pharmacology can be used to study the events underlying the altered theta rhythms resulting from anxiolytics involving multi-level effects including molecular and neural network phenomena. In the behaving animal, hippocampal theta frequency reliably increases with running speed, in a broadly linear fashion, likely tied to spatial coding. Interestingly, anxiolytic drugs reliably reduce hippocampal theta frequency in a consistent way, reducing the offset of the frequency-running speed relationship [85] (see Fig. 2.1) while only minimally affecting the slope of this relationship. Theta rhythm can be studied in the absence of interaction with environment using electrical stimulation to the brainstem in anesthetized rats to activate ascending pathways that control the type II theta component. In this model, increasing strength of stimulation results in a broadly linear increase in theta frequency (See Fig. 2.1b), and all anxiolytic drugs tested in this model [22, 46] reduce theta frequency, whether by reducing the slope or offset of the theta-frequency-to-stimulation relationship. This connection between theta frequency reduction and anxiolytic efficacy suggested to us the use of a spiking neural network model based on experimental data and conductance-based modeling formalisms to help explain and predict biophysical manifestations of anxiolysis. This is investigated in the anxiolytic drug efficacy-predicting context of modifications to the linear relationship between theta frequency and brainstem stimulation level.
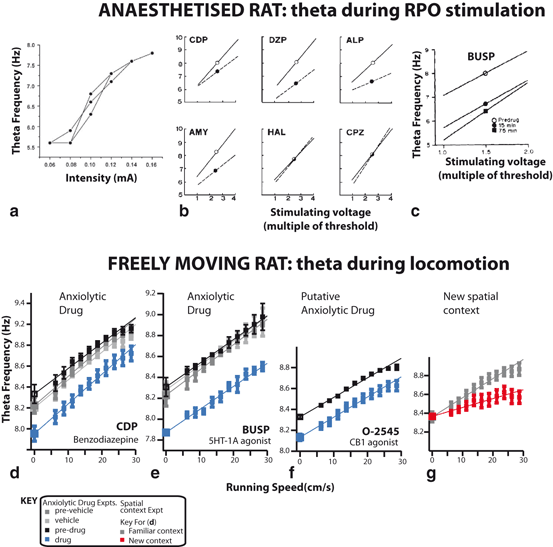
Fig. 2.1
Anxiolytic drugs reduce hippocampal theta frequency. In the anaesthetised rat, anxiolytic drugs reduce frequency of reticular-stimulated hippocampal theta. a Broadly linear relationship between reticular formation stimulation intensity and theta frequency in the anaesthetised rat. Adapted from [66]. b Anxiolytic drugs reduce theta frequency. Open circles indicate baseline, closed circles effect of drug. Adapted from [22]. c Buspirone, later discovered anxiolytic drug acting on 5HT-1A receptors. Adapted from [45]. In the freely moving rat, anxiolytic drugs reduce the intercept of the theta frequency to running speed relationship (d–f), while spatial novelty reduces its slope (d). Three neurochemically-different anxiolytic drugs (all i.p. injections: D, CDP, benzodiazepine agonist, 5mg/kg; E, Buspirone, 5HT-1A agonist, 1mg/kg; F, O-2545, putative anxiolytic, CB1 agonist, 100 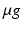 /ml, 0.5ml/kg) have the common effect of reducing the zero cm/s intercept of the theta frequency to running speed relationship. In contrast, exploration of a novel spatial context reduces the slope of this relationship (g), which then recovers as the novel spatial context itself becomes familiar (not shown). Parts f and g present data from the same rats (i.e. a within-subjects double dissociation of intercept and slope effects is observed). Open squares indicate y-intercept of regression lines. All recording sites are from CA1. Adapted from [85]
/ml, 0.5ml/kg) have the common effect of reducing the zero cm/s intercept of the theta frequency to running speed relationship. In contrast, exploration of a novel spatial context reduces the slope of this relationship (g), which then recovers as the novel spatial context itself becomes familiar (not shown). Parts f and g present data from the same rats (i.e. a within-subjects double dissociation of intercept and slope effects is observed). Open squares indicate y-intercept of regression lines. All recording sites are from CA1. Adapted from [85]
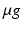 /ml, 0.5ml/kg) have the common effect of reducing the zero cm/s intercept of the theta frequency to running speed relationship. In contrast, exploration of a novel spatial context reduces the slope of this relationship (g), which then recovers as the novel spatial context itself becomes familiar (not shown). Parts f and g present data from the same rats (i.e. a within-subjects double dissociation of intercept and slope effects is observed). Open squares indicate y-intercept of regression lines. All recording sites are from CA1. Adapted from [85]
/ml, 0.5ml/kg) have the common effect of reducing the zero cm/s intercept of the theta frequency to running speed relationship. In contrast, exploration of a novel spatial context reduces the slope of this relationship (g), which then recovers as the novel spatial context itself becomes familiar (not shown). Parts f and g present data from the same rats (i.e. a within-subjects double dissociation of intercept and slope effects is observed). Open squares indicate y-intercept of regression lines. All recording sites are from CA1. Adapted from [85]Methods
A network of spiking neuron models based on time and voltage dependent membrane conductances in the neural simulator software GENESIS is used to investigate the dynamics of theta rhythm frequency control by potential anxiolytic drugs.
Cell Models and Network Structure
Three inhibitory neuron populations were modeled as consisting of single compartment units corresponding to the assumption that spatial integration of inputs to these populations has less contribution to theta oscillation than does space-dependent input to pyramidal cells, which were represented using a multi-compartment model. Time and voltage dependent changes in the conductance of both the spatially uniform inhibitory cell membranes and the spatially distributed pyramidal cell membranes were modeled as time and voltage resistors in resistor-capacitor circuits. The resistance, capacitance, and electromotive force parameters of these circuits are equivalent to experimentally determined membrane properties for each neuron and spatial compartment [24].
Cells modeled that make up the septo-hippocampal system included hippocampal CA1 basket interneurons, CA1 oriens-lacunosum-moleculare neurons, GABAergic neurons projecting from the medial septum to the hippocampus, and CA1 pyramidal cells. Each of these individual neuron models displays many of the firing properties of the neuron they represent, and the connection probability amongst instances of these neuron models come from experimental studies along with a parameter search for a region synaptic strength space demonstrating robust generation of theta rhythm [24].
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree





