The activity of ion channels is fundamental to signaling in the nervous system. Synaptic potentials and action potentials, the basic electrical signals, result directly from the movement of ions through channels. In past decades, patch clamp recording and molecular biology have identified a variety of ion channel types and have begun to clarify the mechanisms underlying channel activity.

The electrical activity of a biologic membrane can be represented as an equivalent circuit consisting of a resistor, a capacitor, and a battery (Fig. 5.1A). This corresponds physically to ion channels, the lipid bilayer, and ion gradients (Fig. 5.1B). The properties of the bilayer and the ion gradients are essentially constant, with the important exception of the Ca²⁺ gradient. In contrast, ion channels vary dramatically among cell types and can open or close in response to physiologic stimuli. The intrinsic membrane properties of a cell and its moment-to-moment electrical activity depend primarily on the types and numbers of ion channels that the cell expresses.

How do the channels, bilayer, and ion gradients work together to produce a membrane potential? A pure lipid bilayer is an excellent insulator, because its hydrophobic interior renders it essentially impermeable to ions. Movement of ions across the membrane (electrically, a current) occurs primarily through ion channels. Because an open ion channel catalyzes the flux of ions down a concentration gradient, it is more intuitive to think in terms of conductance rather than resistance: an increase in the number of open channels produces a higher electrical conductance. The energy source for ion flow through a channel is an ion gradient, resulting from the activity of pumps and carriers, such as the Na⁺ ,K⁺ adenosine triphosphatase (ATPase). Ion flow changes the charge distribution across the membrane. Because like charges repel each other, the presence of net charge in bulk solution is an unstable situation (i.e., principle of electroneutrality). The lipid bilayer is extremely thin (7 nm), allowing strong attractive forces between positively and negatively charged ions on opposite sides of the membrane. This allows the bilayer to act as a capacitor to store charge. The separation of charge across the membrane is the source of the membrane potential (V_M): V_M = Q/C, where Q is the amount of charge, and C is the capacitance of the membrane. Biologic membranes have an essentially constant capacitance, approximately 1 μF/cm2.

The membrane potential depends primarily on the selectivity of the ion channels that are open at a given time. Ion channels can be highly selective for particular ions. For example, many K⁺ channels are more than 100-fold more selective for K⁺ than for Na⁺. For a cell with only K⁺ channels open (i.e., an approximation of a real neuron at its resting potential), a chemical or diffusional force allows K⁺ to diffuse down the concentration gradient and out of the cell. As K⁺ ions flow, however, the outside (o) of the cell becomes electrically positive with respect to the inside (i). Convention defines the voltage outside a cell as zero, so the membrane potential resulting from outward movement of K⁺ ions is said to be negative. That voltage produces an electrical force that prevents further efflux of K⁺ ions, as the excess of positive charge outside the cell repels the positively charged K⁺. If no other ions can cross the membrane, a state of equilibrium is rapidly reached in which the outward diffusional force equals the inward electrical force. That would be a true thermodynamic equilibrium, stable indefinitely without input of metabolic energy. There would be no net flux of K⁺ through an open K⁺ channel. The voltage across the membrane would be the equilibrium potential for K⁺ (E_K), as given by the Nernst
equation for a battery: at 37°C, E_K = 61.5 log([K⁺]_o/[K⁺]_i). E_K is near −90 mV for a physiologic K⁺ gradient.

By the same argument, if only Na⁺-selective channels are open, the membrane potential would be E_Na, or about +60 mV. That is a first approximation to a neuron at the peak of the action potential.

In reality, the situation is more complex, because multiple channel types are open simultaneously. There is no generally valid way to calculate the membrane potential in that case, although two equations are commonly used. The more familiar is the Goldman equation:

V_M = 61.5 log {(P_K [K⁺]_o + P_Na [Na⁺]_o) / (P_K [K ⁺ ]_i + P_Na [Na⁺]_i)}

in which P_K and P_Na are the permeabilities of the membrane to K⁺ and Na⁺ (permeabilities are related to conductances). The derivation of the Goldman equation uses some assumptions that are not realistic for ion channels, particularly that ions move independently of one another, but it is a useful approximation and often serves as an empirical definition of ion permeability.

In another approach, Ohm’s law is used to define the conductance for each ion: for K⁺, I_K = G_K (V_M − E_K). The “driving force,” the difference between the membrane potential and the equilibrium potential, is used rather than the absolute voltage, because the current through an open K⁺ channel goes to zero at the equilibrium potential. If the membrane potential is constant, there must be no net ionic current: I_K + I_Na = 0 (considering only K⁺ and Na⁺). That leads to the “parallel batteries” equation:

V_M = G′_K E_K + G′_Na E_Na

The equation uses normalized conductances G′_K = G_K/(G_K + G_Na) and G′_Na = G_Na/(G_K + G_Na). Qualitatively, the Goldman equation and the parallel batteries equation say that the membrane potential is a compromise among the equilibrium potentials for the individual ions. The higher the conductance (or permeability) for an ion, the closer the membrane potential is to that ion’s equilibrium potential. This allows a better approximation to the situation at rest: the membrane potential is much closer to E_K than to E_Na because many more K⁺ channels are open than Na⁺ channels. The converse is true at the peak of the action potential. For completeness, there is also a delay between channel opening and a change in voltage, because time is required for ion flow to change the net distribution of charge across the membrane (i.e., to charge the membrane capacitance).

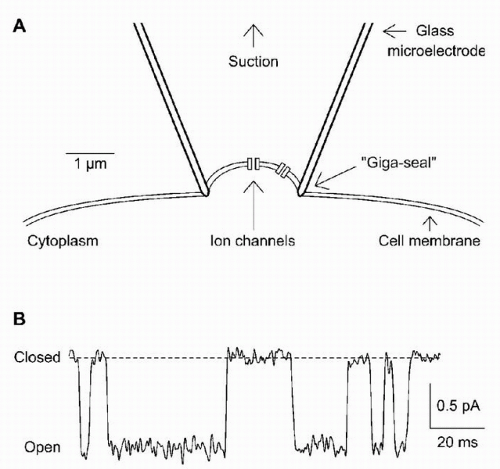
Until 25 years ago, ion channels were considered hypothetical entities. The most direct demonstration of discrete ion channels came from patch clamp recording (Fig. 5.2A). When a glass electrode with an opening of about 1 μm is pressed onto a cell surface, gentle suction often forms a seal between the glass and the cell membrane that is tight electrically, chemically, and physically. The resistance of the seal is typically about 10 GΩ (10¹⁰ Ω). That extremely low rate of ion leakage under the seal implies molecular tightness. The high resistance of the seal gives very low levels of current noise, so that the tiny currents resulting from activity of individual ion channels in the “patch” of membrane directly under the electrode can be resolved. This was one of the first scientific techniques by which the behavior of a single molecule in real time could be observed.

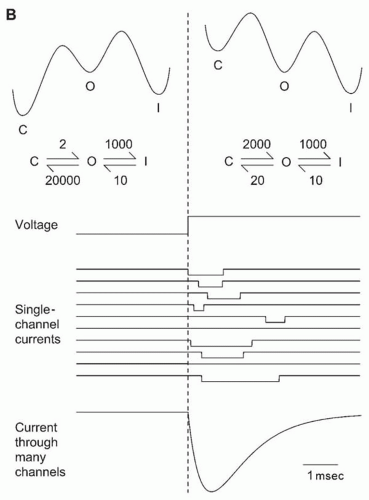
Two types of information can be obtained from single-channel records (Fig. 5.2B): gating (i.e., when is a channel open?) and permeation (i.e., how does current flow through an open ion channel?). A channel’s permeation properties determine its ion selectivity. The absolute amplitude of single-channel currents is also instructive. A typical 2-pA
current may seem inconsequential, but it translates into a flux of 10⁷ ions per second through the channel pore. That simple calculation remains one of the strongest pieces of evidence that an ion channel is a channel, because that transport rate is orders of magnitude higher than the turnover number of even the fastest enzymes and carriers, and the only known mechanism that could produce such a rate is diffusion through a pore, with movement at a rate nearly as fast as if the ions were in bulk water. The combination of high flux and high selectivity among chemically similar ions remains an interesting puzzle.

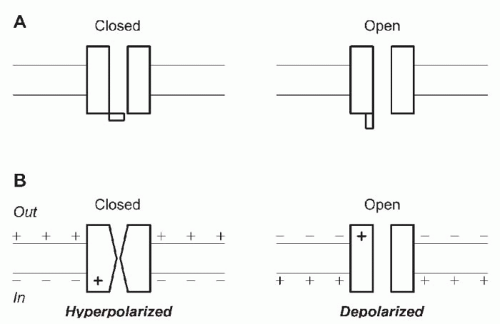
Channel gating is crucial, because the opening and closing of ion channels in response to physiologic stimuli is the fundamental mechanism underlying signals such as synaptic potentials and action potentials. What is gating? Some general conclusions can be drawn from records of single channels (Fig. 5.2B). Channels switch between open and closed states, apparently at random. Under fixed recording conditions, the current observed when a channel is open generally is constant, implying a constant rate of ion movement through the pore. The current through a closed channel is almost undetectable. The transition between the open and closed states is too fast to measure, implying a completed conformational change in a few microseconds or less. Two extreme physical pictures can be used to illustrate gating: literal movement of a gate, a part of the channel protein that can occlude the pore or move out of the way (Fig. 5.3A), or a global conformational change in the protein (Fig. 5.3B). Both mechanisms probably occur.

The observed random opening and closing of channels are precisely what would be expected when a chemical reaction is viewed one molecule at a time (Fig. 5.4). The simplest possible reaction scheme, the closed-open (C-O) model, with first-order transitions linking closed and open states, predicts that the channel will be open a particular fraction of the time, depending on the equilibrium constant for the reaction. The average amount of time that the channel stays in the closed state depends on the rate constant for the C → O reaction. The closed times are highly variable, because the channel must “wait” until thermal energy “pushes” it over the barrier linking the two states. Random does not mean causal, however. Although the duration of any individual closing event is unpredictable, the average behavior of the channel is determined by the rate constants in the kinetic scheme. Real ion channels can exist in considerably more than two states, but the simple two-state C-O model is the starting point for discussion of channel kinetics.

Although useful information can be obtained by recording channel behavior under fixed conditions, the response of channels to changes in conditions allows signaling in the nervous system. Two main factors affect the rates of channel opening and closing: binding of ligands (e.g., neurotransmitters) and voltage. Ligand-gated channels and voltage-dependent channels are functionally and molecularly distinct. The simplest scheme for a ligand-gated channel is a bimolecular binding reaction (Fig. 5.5), in which binding and channel opening are considered to be a single step. This model makes firm predictions: the channel never opens in the absence of ligand, and the channel’s opening rate increases linearly with the ligand concentration. The channel’s mean closed time (for this scheme, the reciprocal of the opening rate) decreases with concentration, and its mean open time does not depend on concentration. As the concentration of ligand increases, the time that the channel has to wait before a ligand binds decreases, enhancing the probability that the channel is open. At very high concentrations, channel closings are extremely brief. These predictions can be tested experimentally. If the tests fail, more states are added to the model, with the ultimate goal being to gain physical insight into the mechanism of channel activation.

Why ion channel gating would depend on voltage is less obvious. Typical membrane potentials are a few tens of
millivolts, but the voltage drop occurs across the extremely thin lipid bilayer. A 70-mV voltage for a 7-nm-thick membrane produces an electrical field of 10⁷ V/m, nearly enough to electrolytically break down even as good a capacitor as a lipid bilayer. The electrical forces on any charged groups in a membrane protein are extremely strong if those charges are in the membrane’s electrical field. That suggests a simple mechanism for voltage dependence. If the closed and open states of a channel differ in their distribution of charge across the membrane (Fig. 5.3B), the equilibrium between the two states will depend on voltage. Only a small number of charges have to move to change the open probability of a channel from near 0 to near 1 over the physiologic range of membrane potentials.

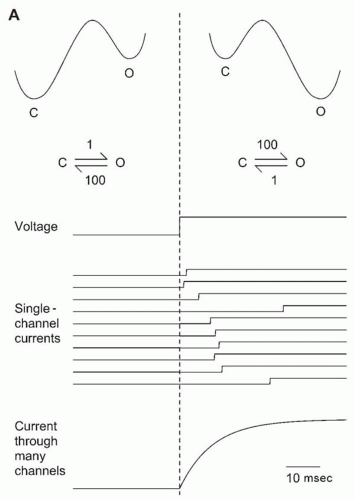
When the voltage changes, voltage-dependent channels do not instantly change from one state to another. Consider the two-state C-O channel (Fig. 5.6A). Suppose that at a negative voltage the rate constants are such that the channel spends 99% of its time closed. For the numbers given, on average, the channel would remain closed for 1 second, and then open for 10 milliseconds before closing again. Suppose that at a more positive voltage the rate constant for channel opening increases and that for closing decreases by 100-fold (for a voltage-dependent channel, both opening and closing rates usually change). The channel will spend 99% of its time open at equilibrium. If the voltage is changed instantly from negative to positive, the rate constants will change instantly, but the channel will require some time to open, as determined by the “new” rate constant. Figure 5.6A illustrates a simulated voltage clamp experiment in which a patch containing a single channel is repeatedly depolarized. At the negative voltage, the channel is nearly always closed at equilibrium. On depolarization, the channel waits a random time (mean, 10 milliseconds) before accumulating enough energy to navigate the barrier to the open state. At equilibrium, the channel is nearly always open at the depolarized voltage. If the experiment is repeated many times, or if an analogous voltage clamp experiment is done on all of the cell’s channels, an exponential relaxation from a p(open) of 0.01 to 0.99 will result, with a time constant of 10 milliseconds. This is a first approximation to the behavior of a voltage-dependent K ⁺ channel of the type involved in the action potential. The rates of channel opening and closing depend on the
height of the energy barriers at each voltage. The absolute rates vary widely among channel types.

The gating of a voltage-dependent Na⁺ channel differs in two crucial ways from that of a K⁺ channel. First, although it also opens on depolarization, the rate constant for opening is approximately 10-fold faster than for the K⁺ channel. Second, during a maintained depolarization, the Na⁺ channel does not remain open. Because this cannot be explained by the C-O model, at minimum, a third inactivated (I) state must be added to the kinetic scheme (Fig. 5.6B). That state is also closed in the sense that no ions go through the channel, but the closed and inactivated states are distinct conformational states of the channel protein.

The next step is to explain how channel opening and closing result in electrical signals. A discussion of the mechanism of the action potential follows.

When a cell with Na⁺ and K⁺ channels is depolarized, both types of channels open, but Na⁺ channels open more rapidly. The influx of Na⁺, net inward movement of positive charge, makes the interior of the cell more positive than before; it depolarizes the cell. The depolarization opens more Na⁺ channels, giving more Na⁺ entry and causing more depolarization (Fig. 5.7). This positive feedback cycle initiates the action potential and is responsible for its all-or-none character. If the cell has sufficient Na⁺ channels, the current generated greatly exceeds the stimulus necessary to trigger the action potential. Once initiated, the action potential is independent of the stimulus.

Termination of the action potential, called repolarization, involves two simultaneous processes. Na⁺ channels inactivate, and K⁺ channels open. Opening of K⁺ channels provides negative feedback (Fig. 5.7); efflux of K⁺ from the cell makes the inside more negative, which tends to close K⁺ channels. The negative feedback contributes to repolarization.

The resting K⁺ conductance of the membrane stabilizes the resting potential. Very small depolarizations do not trigger an action potential. They do not open a large number of Na⁺ channels but increase the driving force on K⁺ (because a depolarized membrane is further from E_K) and decrease the driving force on Na⁺. The net effect of a small depolarization is to increase K⁺ efflux, which leads to hyperpolarization. A sharp boundary, the threshold, exists between small depolarizations that produce only a subthreshold response and slightly larger depolarizations that trigger a full-sized action potential. Threshold is the point at which inward Na⁺ current exceeds outward K⁺ current; the net inward current produces an active depolarization, which initiates further Na⁺ channel opening and the rest of the positive feedback cycle.

The kinetic differences between voltage-dependent Na⁺ and K⁺ channels are crucial to the action potential. During repolarization, K⁺ channel opening and Na⁺ channel inactivation cooperate. Because K⁺ channels also close slowly, the K⁺ conductance of the membrane immediately after repolarization is higher than at rest. The membrane potential is very close to E_K, producing an afterhyperpolarization (AHP).

Our detailed understanding of the mechanism of the action potential is based on the classic experiments of Hodgkin
and Huxley on the giant axon of the squid (1). Current views of the mechanisms of channel gating owe much to the kinetic models they proposed in 1952. That is remarkable, given that the structure of biologic membranes was then poorly understood. Although lipids and proteins were known to be involved, the idea of transmembrane proteins was yet to come. Nevertheless, their descriptions of “permeability changes” can be translated directly into the opening and closing of ion channels. As discussed later, contemporary views of channel gating differ from these original models, but the similarities are impressive.

The Hodgkin-Huxley experimental protocols are the foundation for analysis of ion channel gating to this day. Their basic experiment was to give step changes in voltage (Fig. 5.6). That makes perfect sense now: if a channel is voltage dependent, the first step toward understanding it is to control the relevant variable, the membrane potential. They first defined two kinetically distinct and independent pathways for ion movement, which we now interpret as Na⁺ and K⁺ channels. Ion substitutions played a major role in their separation of Na⁺ and K⁺ currents. For example, Hodgkin and Huxley demonstrated that the Na⁺ current reversed from an inward flow of Na⁺ to an outward current when the axon was depolarized beyond the expected E_Na. That “reversal potential” shifted, as predicted by the Nernst equation, when E_Na was changed by replacing some of the extracellular Na⁺ with an impermeant cation. The reversal potential remains the primary criterion for determining ion channel selectivity. Hodgkin and Huxley also characterized the kinetics of channel opening and closing over the physiologic voltage range. They discovered that Na⁺ channels inactivate and described the voltage dependence of that process.

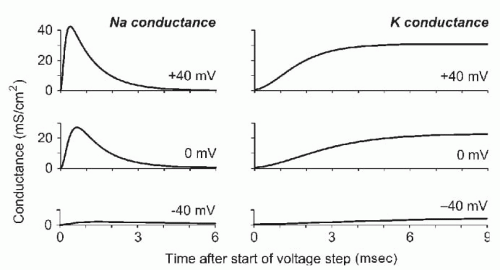
Figure 5.8 summarizes much of their experimental data. Because conductance is roughly proportional to the probability that a channel is open, their data on Na⁺ and K⁺ conductance as a function of voltage and time reflect the kinetics of channel gating. In some ways, the K⁺ and Na⁺ conductances behaved as expected from the previously discussed C-O and C-O-I models (Fig. 5.6), but there were complications. In particular, the time course of activation of the currents was not exponential but showed a sigmoid delay, necessitating more complex kinetic models. No general strategy was available to translate data into a model, and computational limitations encouraged keeping the models as simple as possible.

Hodgkin and Huxley modeled Na⁺ and K⁺ channels as containing four independent gates (1). Each gate behaves kinetically like a C-O channel, but the channel is assumed to be open if and only if all four gates are open simultaneously. The K⁺ channel model is simpler because it is assumed that the four gates are identical. The assumption that the gates are independent simplifies matters, because independent probabilities multiply. If the probability that one gate is open is n, then the probability that a channel is open is n⁴. The requirement for all four gates to open produces the sigmoid delay in the time course of activation of the K⁺ channel (Fig. 5.8).

To explain Na⁺ inactivation, Hodgkin and Huxley assumed that one of the four Na⁺ channel gates is an inactivation gate, with a reverse voltage dependence; it is open at negative voltages and closes at depolarized voltages. The three activation gates open on depolarization, more rapidly than the gates controlling a K⁺ channel. In their equations, m is the probability that a Na⁺ activation gate is open and h the probability that the inactivation gate is open, so that the probability that a Na⁺ channel is open is m³h. The Hodgkin-Huxley model included empirical equations for the voltage dependence of the rate constants for each gate’s opening and closing. That allowed calculation of m, h, and n (and from them, the probabilities that Na⁺ and K⁺ channels are open) as functions of voltage and time. Their model reproduced the experimental data obtained under voltage clamp conditions and generated an action potential when the membrane voltage was not controlled. Like a real action potential, the computed action potential had a threshold, the ability to propagate, and a refractory period.

The diversity of electrical activity patterns is matched or exceeded by the diversity of ion channel types (3). Channels were initially distinguished electrophysiologically at the level of whole-cell currents or single-channel gating, but it is now evident that considerable molecular diversity exists among voltage-dependent ion channels. Major goals today are to correlate the different ion channel types identified by physiologic and molecular techniques and to determine how their functions relate to their structures. Ion channels are classified by ion selectivity, kinetics of channel gating, pharmacology, and molecular characteristics.

Information is available on the amino acid sequence, higher-order structure, and transmembrane topology of numerous channels (Fig. 5.9). Difficulties in obtaining structural data on membrane proteins have prevented atomic-level resolution of the structure of most channels. One spectacular exception is the crystal structures of bacterial K⁺ channels (7, 8, 9). Those channels are members of a large superfamily of channel proteins with deep evolutionary roots (3,10) that has diverged to produce voltage-dependent
K⁺, Na⁺, and Ca²⁺ channels, among others. The bacterial K⁺ channels share a P loop with voltage-dependent channels, which forms the selectivity filter near the extracellular side of the pore. The structures are likely to be applicable to many other channel types and have implications for mechanisms of permeation (11) and gating (12,13). Unfortunately, the crystal structure of a bacterial voltage-dependent K⁺ channel (14) places the voltage sensor in a location that seems inconsistent with a variety of functional data (15,16), so a molecular understanding of voltage-dependent gating remains a goal for the future.

K⁺ channels are remarkably diverse. Physiologically, perhaps a dozen kinetically or pharmacologically distinct types are known, and more than 70 genes produce K⁺ channels when expressed in vitro (17,18) (Table 5.1). To some extent, this makes sense, because K⁺ channels perform a variety of physiologic functions. They set the resting potential, repolarize the action potential, affect the threshold for generation of the action potential, and regulate a cell’s ability to fire repetitively. K⁺ channels can sense metabolic activity by way of Ca²⁺ or adenosine triphosphate (ATP). K⁺ channels can be modulated, often through G-protein-coupled receptors for hormones and neurotransmitters, by direct interaction with G-protein subunits or by phosphorylation (19,20).