Communication Within Neurons
 Although it had been known for nearly 2000 years that nerves served to communicate between the body and the brain, the question of how they did it was settled only a matter of decades ago. Nervous conduction is now one of the best-understood processes in the whole field of physiology, and its elucidation has been a major triumph for that branch of the subject known as biophysics – the application of purely physical methods to biology.
Although it had been known for nearly 2000 years that nerves served to communicate between the body and the brain, the question of how they did it was settled only a matter of decades ago. Nervous conduction is now one of the best-understood processes in the whole field of physiology, and its elucidation has been a major triumph for that branch of the subject known as biophysics – the application of purely physical methods to biology.Neurons and electricity
That there was some link between electricity and nervous and muscular action had been sensed as far back as the end of the eighteenth century, with Galvani’s celebrated observation of the twitching of frogs’ legs when in contact with certain combinations of metals.  Further understanding had to wait for the development of galvanometers sensitive enough to register the passage of very small electrical currents. By the end of the nineteenth century it was clear not only that nerves and muscle could be activated by electrical stimulation, but conversely that their normal activity was always accompanied by changes in electrical potential. It did not follow, of course, that these electrical changes were the cause of neural communication, since activity of many other kinds of tissue also gave rise to electrical effects. It was not until some 70 years ago that it was finally established that electrical currents were not only generated as a side-effect of nervous conduction, but were also necessary for conduction to take place at all.
Further understanding had to wait for the development of galvanometers sensitive enough to register the passage of very small electrical currents. By the end of the nineteenth century it was clear not only that nerves and muscle could be activated by electrical stimulation, but conversely that their normal activity was always accompanied by changes in electrical potential. It did not follow, of course, that these electrical changes were the cause of neural communication, since activity of many other kinds of tissue also gave rise to electrical effects. It was not until some 70 years ago that it was finally established that electrical currents were not only generated as a side-effect of nervous conduction, but were also necessary for conduction to take place at all.
 Further understanding had to wait for the development of galvanometers sensitive enough to register the passage of very small electrical currents. By the end of the nineteenth century it was clear not only that nerves and muscle could be activated by electrical stimulation, but conversely that their normal activity was always accompanied by changes in electrical potential. It did not follow, of course, that these electrical changes were the cause of neural communication, since activity of many other kinds of tissue also gave rise to electrical effects. It was not until some 70 years ago that it was finally established that electrical currents were not only generated as a side-effect of nervous conduction, but were also necessary for conduction to take place at all.
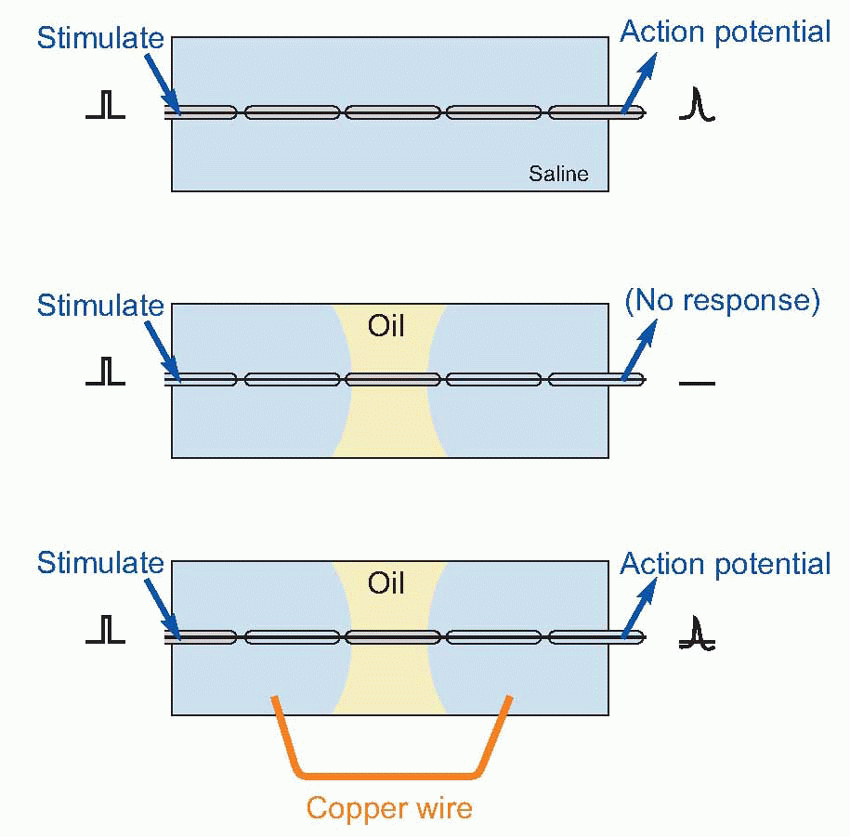
Further understanding had to wait for the development of galvanometers sensitive enough to register the passage of very small electrical currents. By the end of the nineteenth century it was clear not only that nerves and muscle could be activated by electrical stimulation, but conversely that their normal activity was always accompanied by changes in electrical potential. It did not follow, of course, that these electrical changes were the cause of neural communication, since activity of many other kinds of tissue also gave rise to electrical effects. It was not until some 70 years ago that it was finally established that electrical currents were not only generated as a side-effect of nervous conduction, but were also necessary for conduction to take place at all.A simple demonstration will convince even the most hardened sceptic of this. Dissect out a short length of myelinated nerve fibre, and lay it in a pool of saline solution on a glass slide. Stimulate one end while recording from the other: you pick up the action potentials that are transmitted down the axon. Now introduce a pool of (non-conductive) oil across the middle of the slide, dividing the saline into separate pools at each end. Stimulate again: there is no response. Yet we have done nothing to the interior of the fibre, so nerve conduction cannot be due to movements of fluids or of filaments within the axon. Next, join the two pools of saline together, with a copper wire. Suddenly the fibre starts conducting again. Something, passing along the copper from one pool to the other, must have enabled this to happen. Heat is too slow: the only possible candidate is electricity, completing the circuit of which the other half lies within the axon. In other words, the current generated by an active nerve is not just an accidental by-product of transmission, like the noise from a car: it is an essential determinant of the entire process.
 |
The flow of electrical current along nerves
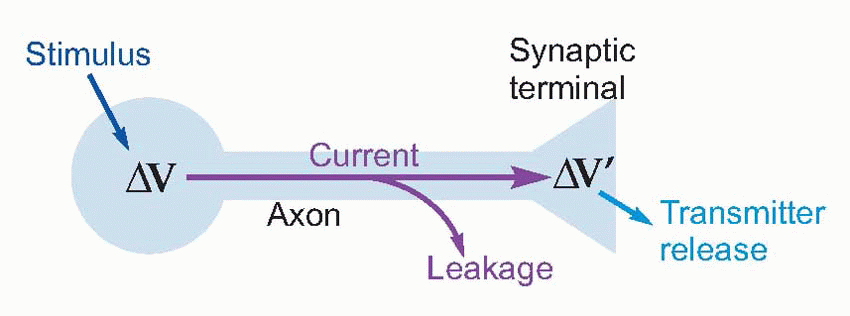
Now nerve fibres, with their conductive central core of axoplasm surrounded by an insulated membrane often reinforced with extra non-conductive layers of myelin, are clearly very like ordinary insulated wires: if you apply a voltage at one end, current flows down the core and
should make the other end change its voltage as well, and thus trigger transmitter release. Could nerve signals simply be transmitted by this kind of passive conduction, in the same way that messages pass along a telephone wire?
should make the other end change its voltage as well, and thus trigger transmitter release. Could nerve signals simply be transmitted by this kind of passive conduction, in the same way that messages pass along a telephone wire?
 |
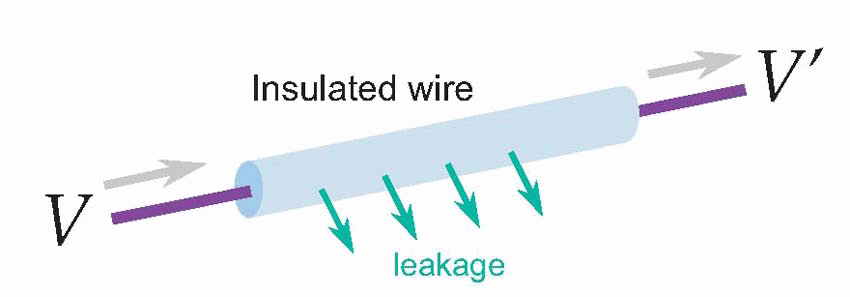
For most nerves, the answer is no. The snag is leakage. We’re used to electrical wires and cables in which the core is a very good conductor – it has a low resistance – and the outside is a very good insulator – has a very high resistance. So if you apply a given voltage δV at one end you get essentially the same voltage δV’ at the other end. But not exactly the same voltage, because a little of the current will have leaked out of the wire along the way, so the current leaving the far end is slightly less than the current entering. With ordinary insulated wires like the ones used for domestic wiring very little current is lost, but nevertheless some is, and you notice it if you’re trying to conduct over very long distances. For the Victorian engineers who laid the first transatlantic telegraph cables this loss was a severe problem. You might apply quite large voltages to your cable in Penzance and find by the time they reached Nova Scotia that practically nothing was left – the electricity had just leaked away into the Atlantic. You need to understand leakage a little more quantitatively, because it underlies how a nerve fibre actually works, and this involves a little physics: more precisely, something called its cable properties.
 |
Nerve fibres as cables
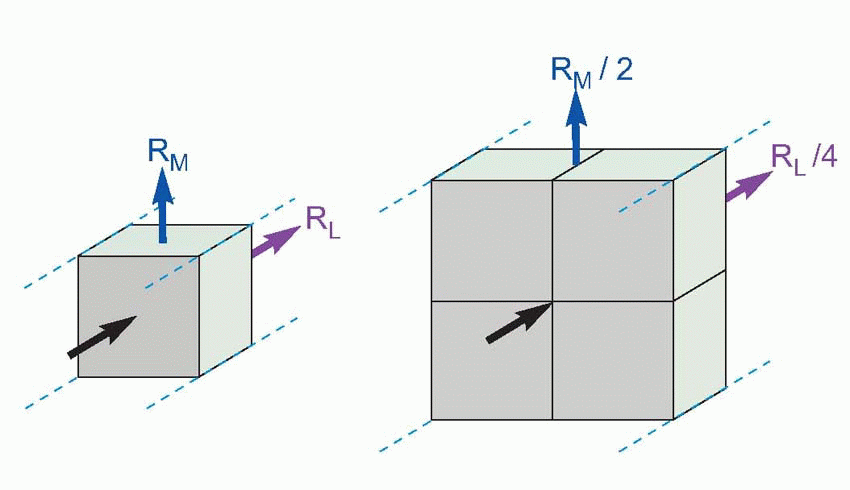
Imagine the axon sliced up into a series of little imaginary compartments or units. For each unit, the current has a choice (red arrows): it can either leak away across the membrane, or carry on to the next unit. What it actually does depends both on how good its insulation is – the resistance of the axon membrane – and also on how much resistance is offered to currents flowing longitudinally through the axoplasm. We can call the transverse, insulating, resistance of the membrane for one unit RM, and the longitudinal resistance of the axoplasm per unit RL. Joining lots of these units in series, we get a ladder-like network of resistors called the equivalent circuit of the nerve fibre. We can assume that the external medium offers no significant resistance to current flow (the justification for this assumption will become apparent later), and treat all the outer ends of each individual RM as if they were in electrical continuity.
 |
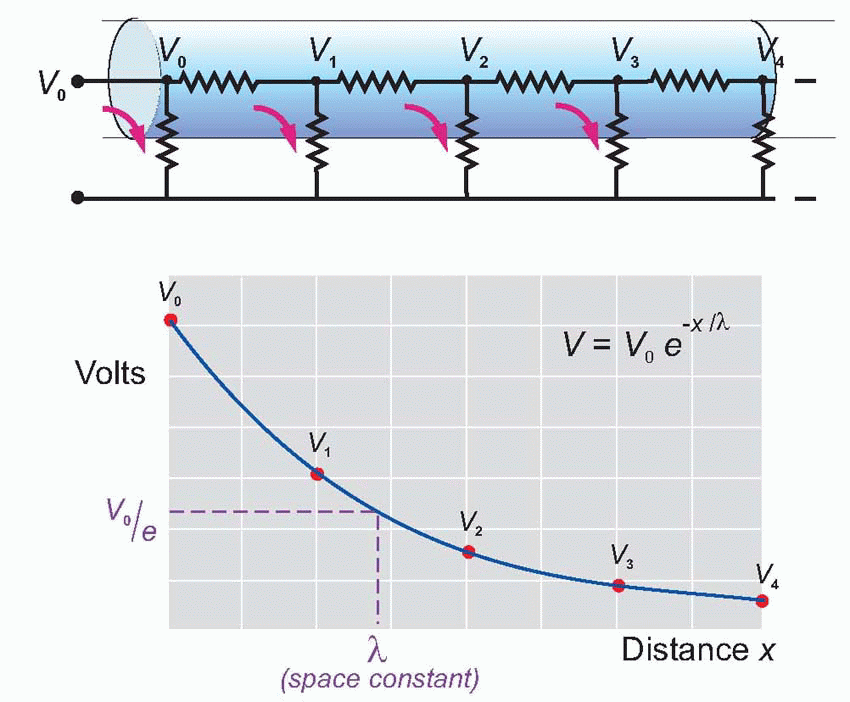 |
Now imagine a potential V0 applied to the end of this ladder. The current entering the first compartment has a choice: it can either flow out through RM or continue through RL to enter the next compartment. In fact, some fixed fraction of the total current takes the former route and the rest takes the latter: the bigger the resistance of the membrane, RM, and the smaller that of the axoplasm, RL, the greater will be the tendency of the current to carry straight on rather than leak away through the membrane. Unless the insulation is perfect, or the axoplasm infinitely conductive, the current entering the second cell will be smaller than that entering the first by some fixed ratio. In the same way, the current entering the third cell will be smaller than that entering the second, and so on all the way down the chain. The result is that the potential seen at each compartment will fall in a fixed ratio as one goes from compartment to compartment down the line, resulting in an exponential decline in voltage as a function of distance along the axon, at a rate that will depend on the ratio RM/RL. Thus V is given by V0e-x/λ, where e is the well-known constant whose value is about 2.718, and λ is a fundamental parameter called the space constant that
describes how quickly the voltage declines as a function of the distance x. λ is in fact the distance you have to go before the voltage has dropped to 1/e (about 37 per cent) of its original value Vo. It turns out in fact that λ is actually equal to .
. 
describes how quickly the voltage declines as a function of the distance x. λ is in fact the distance you have to go before the voltage has dropped to 1/e (about 37 per cent) of its original value Vo. It turns out in fact that λ is actually equal to
 .
. 
For telephone wires this space constant works out at some hundreds of miles, and doesn’t present much of a problem. But the performance of nerves, unfortunately, is a bit of a disaster. Consider for instance a large myelinated frog nerve fibre, say 14 µm in diameter, and assume for the moment that the myelin is uninterrupted along its length, without nodes of Ranvier. The axoplasm is intrinsically a vastly better conductor of electricity than myelin: their specific resistances are of the order of 100 ohm cm and 600 megohm cm, respectively. But because the crosssectional area of the axoplasm is so small, the ratio of RM to RL is not very great: for 1 mm, RM comes out as about 250 megohm and RL about 14 megohm, giving a space constant of some 4 mm or so. In other words, a potential generated at one end of the axon will have dropped to less than half at a distance of 4 mm, to about a tenth of its original value after a centimetre, and by 2 cm will only be some 1 per cent of the original stimulus, and probably undetectable in the general background electrical noise. In other words, axons are quite incapable of acting as reliable passive conductors of electricity over distances of more than a centimetre or two at most. In many parts of the brain and in some sense organs, for example within the thin layer of the retina, a space constant of this size is fine. But if you’re trying to get a message from your spinal cord to your feet it is obviously absolutely hopeless.
There are two reasons for this disappointing behaviour. The first is that the materials that nerve fibres have to be made of are not ideal. The core conducts about 50 times worse than it if it were made of say copper, while the insulating part, the cell membrane, is absolutely hopeless: compared with say rubber, its degree of insulation is about a million times worse. The other reason is that nerves are exceedingly small, and the layer of insulation extremely thin. Size has a very important effect on the space constant: if you double the diameter of a cable, RM drops by half (it depends on the surface area) but RL drops by a quarter, because it depends on the cross-sectional area, which varies with the square of the diameter. As a result, the ratio RM/RL is doubled, so the space-constant increases by only the square root of 2. In general the space constant is proportional to the square root of the diameter: the bigger the nerve the further it can conduct. However, there are obviously constraints on how much you can improve nerves this way. Consider the sciatic nerve in your leg, whose large, 10 µm, fibres have space constants of a couple of millimetres or so. Even if we increased the diameter of each fibre to 1 cm, the space constant would still only be some 15 cm: messages would fade out before they got half-way down your thigh. You can calculate for yourself that such a fibre would need to be something like 9 cm across to be able to conduct reliably all the way down your leg, but the nerve would then be as big as the leg itself! (This analysis is not quite fair because we have assumed a constant thickness of myelin: but even if we allow this thickness to increase in proportion with the axon itself, the fibre will still need to be almost a hundred times bigger. Bearing in mind the fact that many important fibre tracts in the body contain millions of fibres, one must still conclude that passive conduction is not a practical possibility over long distances.)
 |
For most nerves, then, passive conduction is not an option. How Victorian engineers solved the same problem in long telegraph cables was to have little amplifiers at intervals, called repeaters, which regenerated the signal, building the voltage up again each time to a full size. Since these repeaters used external energy to do their work, this was a process not of passive but of active conduction.
How does the nerve do it? It too has repeaters. In nerve fibres that have to conduct over long distances there are channels in the membrane that open in response to small changes in voltage across the membrane – called voltagegated channels. When they open they trigger off a very large voltage burst or spike, with a fixed size of some 100 mV in amplitude but only 2-3 ms in duration: this dramatic and explosive event is called an action potential.
Action potentials
Regeneration
Many properties of action potentials demonstrate this process of regeneration. If we record the action potential from a single electrical stimulus at different points along a nerve fibre, we find that its amplitude does not in fact decrease at all as a function of distance, but stays at a constant value. Even more strikingly, the size of this action potential is not even a function of the size or nature of the stimulus that initiated it in the first place. So long as the strength of the stimulus is above a certain threshold value (below which no action potential is seen at all), neither the amplitude nor shape nor speed of the action potential is in any way influenced by the nature of the original stimulus, a property known as the all-or-nothing law. These two features, the all-or-nothing law and the existence of a threshold, are never shown by passive conduction, where the energy for the transmitted signal must come entirely from the original stimulus.
A familiar example of this kind of behaviour is a burning sparkler. Here the combustion is continually regenerative: the heat of the burning region raises the temperature of the next region to the point where it too catches fire, and so on all along its length. In other words, there is a continuous cyclic process in which heat triggers combustion and combustion generates heat, this heat coming of course from the chemical energy stored in the sparkler’s coating. The temperature and rate of advance of the burning region are not functions of the temperature of the flame which originally ignited it, so long as this was sufficient to light it at all.
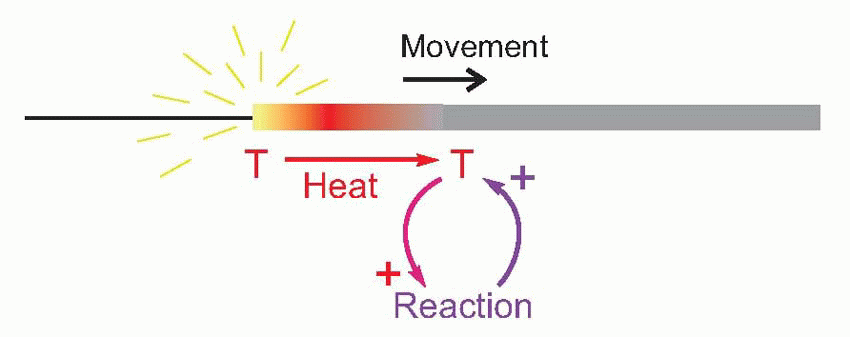 |
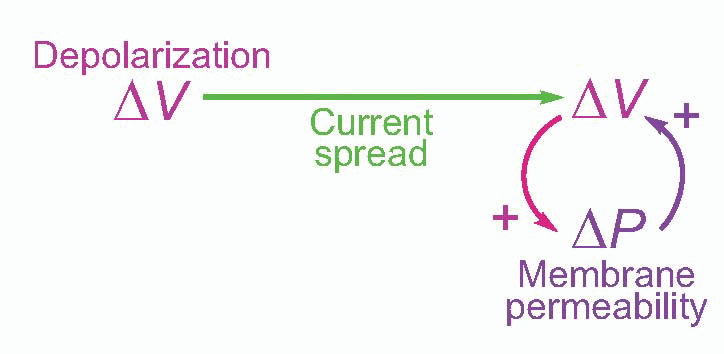
It turns out that this is a surprisingly close analogy to the mechanism of propagation of the action potential. What happens is that the original stimulus to the fibre, δV, makes local currents flow passively through the membrane, causing the potential to spread. It is sensed by neighbouring regions of the fibre and triggers a mechanism in the membrane that generates a voltage many times larger (thus introducing an amplification of the original signal), which in turn sets up local currents that cause a potential change still further down the axon … and so on, until the potential change has been transmitted from the point of stimulation to the end of the axon. This whole cyclical process is known as the local circuit mechanism of action potential propagation.
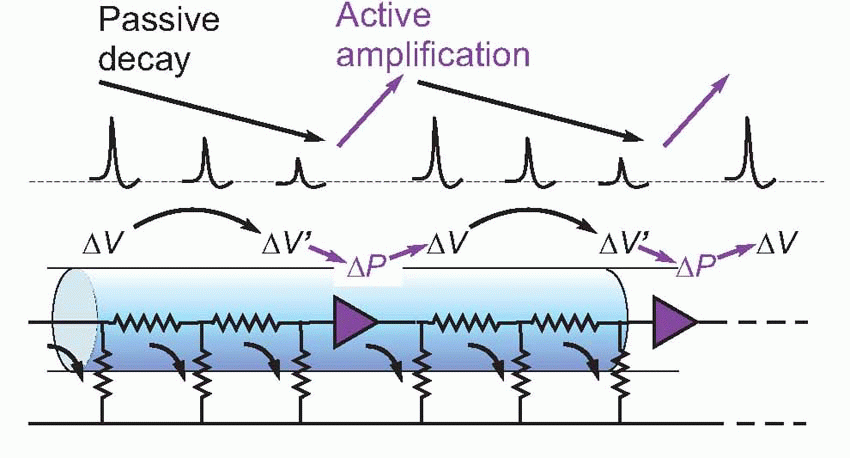 |
Each cycle consists of three distinct stages: first, there is the mechanism by which a potential at one point results in a passive flow of current and thus in depolarization of regions further down the axon; second, the mechanism by which this depolarization triggers off some change in the membrane; and third, the mechanism by which this change produces a new depolarization that is much larger than what originally triggered it off.
Now of these processes, the passive part of conduction – current flow – was understood very early on: it is simply a matter of physics, and in this respect nerve behaves in exactly the same way as the telephone and telegraph cables whose properties had been sorted out since the end of the nineteenth century, and can be described in terms of equivalent circuits. The other two processes obviously require identification of this mysterious change in the membrane that results in amplification of the voltage that triggers it. It turns out that this change consists in a change in the permeability, δP, of the membrane to certain ions. If we measure the electrical resistance of the membrane, we find that during an action potential it drops enormously – with a timecourse not very different from that of the action potential itself. To understand how a change in permeability can affect potential, we need first to understand the ionic composition of the interior of nerve fibres, and the fluid by which they are surrounded.
 |
Ionic concentrations
From a physiological point of view, the body’s function is ultimately to provide a cosy and comfortable home for our genes, where they can feel safe. Genes require complex biochemical machinery to make them work, and this machinery in turn has quite stringent requirements in terms of the concentrations of ions and other substances that need to be around. This of course is why we evolved cells; and in their membranes are all the mechanisms that carry out cellular homeostasis, particularly of their ion concentrations. But cells simply adrift in their environment are still at the mercy of environmental change. So the second major stage in evolution was the building of cells into tissues and bodies, which can then seal themselves off from the harsh world outside, and create a sort of inner environment tailor-made to suit the cellular requirements. As a result we have a nested series of compartments: intracellular containing intracellular fluid (ICF), extracellular with its ECF, and finally the real environment. Our genes are doubly buffered, like gold bullion locked in a safe inside a vault in Fort Knox. The brain is particularly well protected, through the blood- brain barrier (the tight junctions between astrocytes that separate cerebral capillaries from neurons) and buffering effect of the cerebrospinal fluid (CSF), which is in ionic equilibrium with brain ECF and whose composition is actively maintained by transport processes in the choroid plexus.
Table 2.1 Ionic composition of two kinds of electrically active cell | |||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| |||||||||||||||||||||||||||||||||||||||
 |
ICF differs from ECF in a number of ways, that vary slightly from one cell to another, and between species, but the underlying pattern is very similar. The single most important feature is that inside an axon we have a lot of potassium and not much sodium, whereas ECF is the opposite, with a lot of sodium and not much potassium. ECF or blood is in many ways remarkably like seawater. Or perhaps not so remarkable when you realize that it was in the ocean that cells first evolved into multicellular organisms: you are a walking bag of seawater, your cells still rocked in the cradle of the deep. 

These differences in concentration are maintained in two ways. The composition of the ECF by overall homeostatic mechanisms involving such things as the kidney and the regulation of intake, mechanisms with which we shall not be concerned until Chapter 14, when we discuss how they are themselves regulated by the brain. The differences between ICF and ECF that are so striking in that table are the result of specific mechanisms that reside in the membrane of the cell. What can be deduced about the membrane from those differences? For a start, it must be essentially impermeable to all these ions: otherwise there would be nothing to stop Na and K from simply swapping with each other, so eventually there would be no difference in concentration at all. Second, the membrane must have set these particular concentrations up in the first place, presumably by manipulating the movement of ions across it.
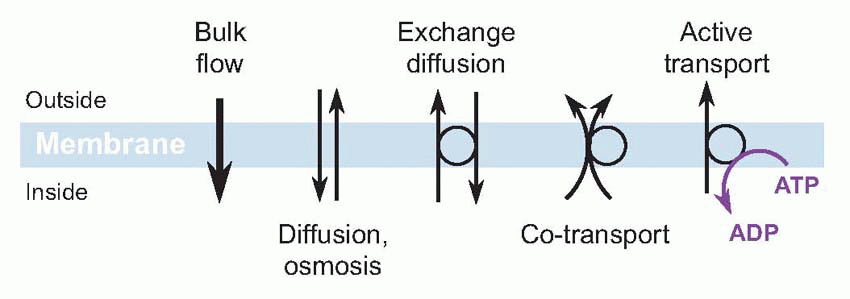
The impermeability of the cellular membrane is a fundamental consequence of its construction, as a bilayer of phospholipid molecules, with hydrophilic heads pointing outwards and hydrophobic tails forming the jam in the sandwich. Such a structure ought not to let water or ions across. But floating in it are large and ugly molecules – proteins or glycoproteins – that in effect provide passages or tunnels that let small molecules through, in a controlled and specific manner. Now there are several different ways an ion can cross a cell membrane, but for the moment we shall just consider two major categories: passive and active. Given the chance, ions will always flow passively down a concentration gradient: in this passive diffusion, from high concentration to low, the ion necessarily loses energy. Conversely, if you see an ion moving up its energy gradient, it is gaining energy that must have come from somewhere: this is called active transport, and uses adenosine triphosphate (ATP). From the nerve fibre’s point of view, by far the most important of these membrane processes is what biochemically minded people think of as a sodium-potassium ATP-ase but which physiologists – loosely – refer to as the sodium pump.
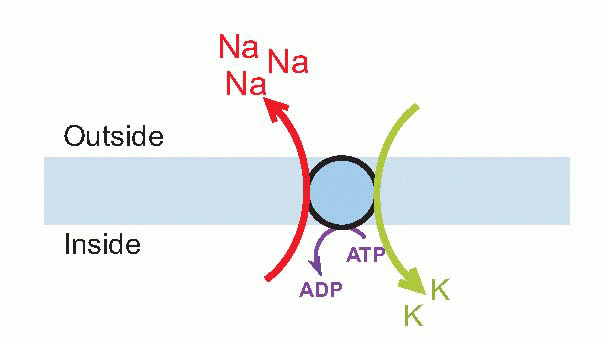
The sodium pump
What it does is swap sodium ions on the inside with potassium ions on the outside (actually three sodiums for two potassiums). Because in each case this means moving ions against their concentration gradient, such pumps consume energy – hence the ATP-ase activity. (It is composed of a rather complicated protein straddling the membrane – it actually crosses it 10 times – and a protruding glycoprotein: the protein part has a number of functionally significant sites – a sodium-binding site, a potassium-binding site, and inside, another region that acts as an ATP-ase.) The sodium pump is not just found in excitable cells like nerve and muscle, for its primary
function is not really electrical at all. This can be seen by blocking the pump, for instance with a substance called ouabain, a cardiac glycoside found naturally in certain plants in Africa, where it has been used as an arrow poison. What then happens is that the normal background leakage of sodium into the cell is no longer baled out, and potassium is similarly gradually lost. Because the gain of sodium is faster than the loss of potassium, chloride moves with it to preserve neutrality, and water is drawn in osmotically. As a result, the cell begins to swell and eventually bursts. In other words, the pump is essential to maintain osmotic equilibrium.
function is not really electrical at all. This can be seen by blocking the pump, for instance with a substance called ouabain, a cardiac glycoside found naturally in certain plants in Africa, where it has been used as an arrow poison. What then happens is that the normal background leakage of sodium into the cell is no longer baled out, and potassium is similarly gradually lost. Because the gain of sodium is faster than the loss of potassium, chloride moves with it to preserve neutrality, and water is drawn in osmotically. As a result, the cell begins to swell and eventually bursts. In other words, the pump is essential to maintain osmotic equilibrium.

 |
What this and the many other varieties of pump also achieve is the creation of a store of potential energy. The membrane is like a car battery, charged by the dynamo provided by the sodium pump. This constant charging incurs a heavy metabolic cost – some 20 per cent of the resting energy consumption of the brain. It is rather a special energy store, in two respects. First, that unlike other stores in the body such as glycogen or fat or even ATP, this store is available for instant use – within a fraction of a millisecond. This makes it ideal for rapid nerve conduction. Second, that it is specifically available at the membrane of the cell, where it can be used for tasks that are themselves localized in the membrane. Many cells use this energy for transporting other substances, through coupled transport: sodium’s desire to enter the cell, down its concentration gradient, can for instance be coupled to the transport of glucose. Potassium is not used in this way, and in fact the axon membrane is characterized by being slightly permeable to potassium in its resting state, through one or more kinds of potassium leakage channels. We shall see later that these channels have an important role in determining the electrical properties of the axon at rest.
 |
Clinical box 2.1 The importance of the distribution of ions
The fluid surrounding cells is, as far as ions are concerned, in direct continuity with the blood. Hence, any change in the blood ionic composition leads to a change in the extraneuronal ionic concentration, and, correspondingly, the concentration gradient across the neuronal membrane. We know that the distribution of ions across the membrane determines the electrical properties of the neurons and it follows that disturbance in blood Na, K or Ca concentration will have profound neurological sequelae.
Indeed, hypokalaemia, by hyperpolarizing the myocyte membrane (which has very similar properties to the neuronal membrane) causes motor weakness which can be severe enough to cause paralysis and respiratory failure. Hyperkalaemia usually manifests through its effect on electrical conduction in the heart, causing dysrhythmia and death. In contrast, severe hypernatraemia (perhaps from severe dehydration) can lead to cerebral depression and sedation, and further to coma and death. Conversely, patients with hyponatraemia (for example after success at water-drinking competitions) are prone to developing seizures. Interestingly, rapid restoration of extracellular sodium following prolonged hyponatraemia can be fatal as the rapid osmotic changes that ensue can lead to irreversible neuronal injury.
Hypercalcaemia is a curious case; calcium is essential for muscle contraction, neurotransmitter release and membrane channel function. One might therefore assume that hypercalcaemia is associated with seizures, tingling and neuronal hyperactivity. Instead the converse is true; hypercalcaemia is associated with weakness, drowsiness and reduced bowel motility. The reason for this is that calcium is predominantly an extracellular ion, and the membrane, having the properties of a capacitor, tends to accumulate these cations on the outer surface. This causes the local transmembrane electrical potential to be augmented, effectively hyperpolarizing the cell membrane and reducing electrical transmission.
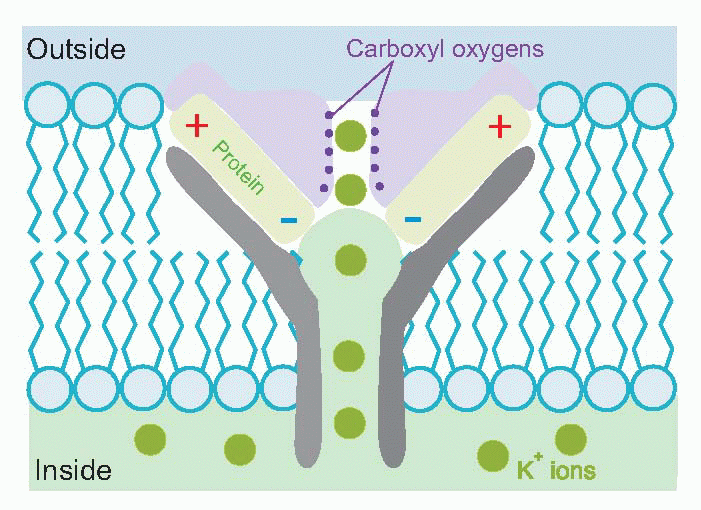
One might well wonder how it is possible to have a channel that is specifically permeable to potassium and not to sodium, an ion which is also singly positively charged and has a smaller hydrated size. Recent studies of the molecular structure of particular potassium channels have demonstrated a complex structure almost perfectly designed for this task. Negative charges associated with the channel proteins lure in positive ions, while carboxyl oxygens substitute for the water to which the ion is normally wedded: unhydrated sodium, being bigger than unhydrated potassium, is then excluded.
This then is the ionic backdrop against which the axonal membrane operates. Much of its operation is common to all cells. As we shall see, they all share physical mechanisms that convert any changes in membrane permeability to changes in potential. What is unique about nerve and muscle cells is that they also possess special mechanisms by which changes in permeability are in turn triggered by changes in potential, thus completing the cycle of three links by which the action potential is propagated over the membrane surface. Thus to understand how nerves work we need to be able to answer two questions:
How do ionic permeabilities affect membrane potential?
How do membrane potentials affect ionic permeabilities?
How potential depends on ionic permeabilities
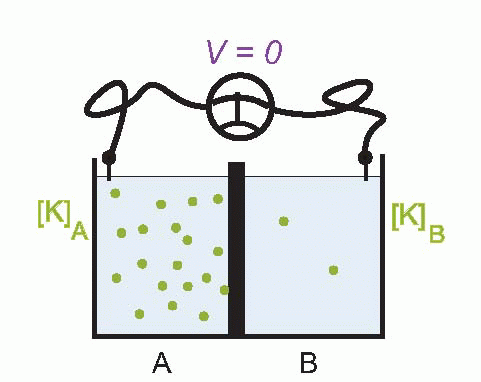
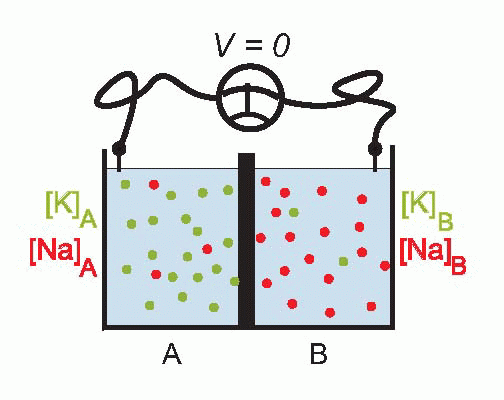
Imagine that we have a system of two compartments, A and B, and that initially A contains a strong solution of potassium chloride, and B a weak one. Now suppose that the membrane separating them, initially impermeable, suddenly becomes permeable to potassium ions. Clearly there will now be a tendency for K+ to diffuse through the membrane down the concentration gradient between A and B. Since the ions carry a positive charge, compartment B will become more and more positive with respect to A as they migrate in this way, setting up an electrical gradient that will tend to oppose the entry of further ions from A. Eventually there will come a point where the concentration gradient from A to B will be exactly equal and opposite to the electrical gradient from B to A, and the system will be in equilibrium, since there will be no net flow of ions across the membrane.
 |
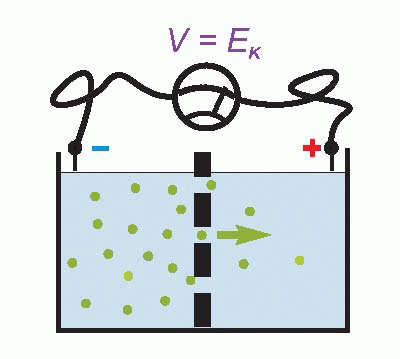 |
The resultant electrical potential between A and B is then called the equilibrium potential for potassium, EK. To work out how big this potential will be, consider the energy involved in moving one potassium ion from A to B. The work done in moving it against the electrical gradient will be given by its charge e multiplied by the potential difference EK; since the system is in equilibrium, this work must be exactly equal to the energy gained in moving down the concentration gradient, which can be shown to be
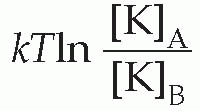
where T is the absolute temperature, and k is Boltzmann’s constant. So we can write:

Therefore

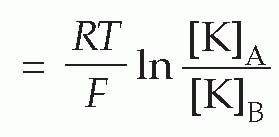

(In the alternative form, derived from consideration of a mole rather than a single ion, R is the gas constant, and F is Faraday’s constant, equal to N.e.) This relationship (the Nernst equation) is true for any ion in equilibrium across a membrane to which it is freely (and solely) permeable, with the proviso that if the charge on the ion is not +1 (as for instance in the case of Cl− or Ca2+) we need to include this ionic charge z as well:
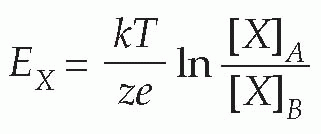
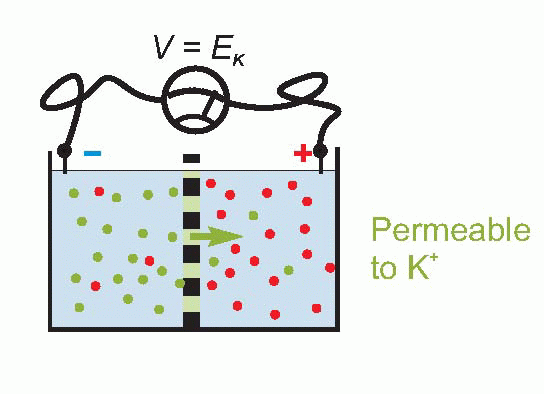
Only a tiny number of ions need to cross the membrane to set up such an equilibrium, so that the concentrations of the ions on each side remain effectively unchanged, and the equilibrium potential is set up virtually instantaneously after a sudden permeability change of this kind. Suddenly making the membrane permeable to potassium – perhaps by opening up channels that allow K+ through but nothing else – is rather like connecting a battery of voltage EK across the equivalent circuit on p. 19.
Now we noted earlier that the axonal membrane at rest is indeed slightly permeable to potassium. Since – taking the figures for the squid giant axon – the concentration of potassium inside is about 20 times greater than outside, we can calculate that there ought to be an equilibrium potential across the membrane of some 75 mV, negative inside. If you actually put an electrode into a squid axon and measure the potential, you do indeed find a standing negative voltage, the resting potential, which is of the right order of magnitude but a little smaller (some -60 mV). The discrepancy tells us that our equations need to be refined.
Permeability to more than one ion
The limitation of the Nernst equation is that it represents a highly idealized – indeed hypothetical – state of affairs, because at any one moment, real membranes are in fact permeable to more than one ion. Let us go just one step further and imagine a situation of two compartments just as before, and different concentrations of sodium and potassium on the two sides. This time, instead of being permeable to just one of the ions, suppose it now becomes permeable to both. One thing we can deduce at once is that is that the overall potential, V, will not just be a function of the concentration differences of the ions. It must also depend on just how permeable the membrane is to each of them.
 |
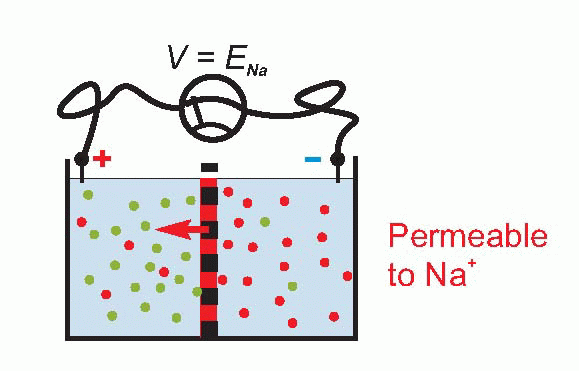
To see that this must be so, consider an extreme case – suppose that we make the permeability to sodium smaller and smaller and smaller, so that eventually it reaches zero. Then V must be given by EK = 58 log10 [K]A/[K]B, or about -75 mV. Equally, if we make the permeability to potassium smaller and smaller, to zero, then V will be given by ENa = 58 log10 [Na]A/[Na]B , or about +55 mV. So the overall potential must also depend on the permeabilities of the two ions, which we can call PK and PNa. These are called permeability coefficients, and represent the ease with which the ion can pass through the barrier for a given concentration ratio.
 |
 |
Because of the Ps, the resultant equation for the voltage V, the Goldman constant field equation, is a little more complicated than the simple Nernst equation, but not very.

It has the same general form, but as you would expect we now have terms for both ions, and they are multiplied by their respective Ps. So in a sense their weighting in the expression depends on how permeable they are. The more permeable the membrane is to potassium, the more the potassium concentration ratio will matter; and in the limit, if we reduce one of the permeabilities to zero, something magical happens – it turns into the Nernst equation. So in a sense the Nernst equation is simply a special case of this one.
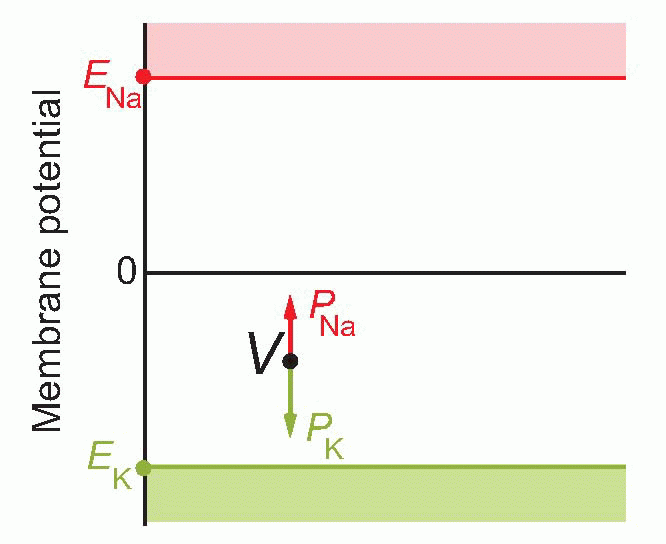
If you’re not very happy even with this sort of elementary maths, there is a graphical representation which most people find a helpful way of looking at it. In a sense, EK and ENa represent extreme values of the range that V can take up: can’t get more positive than ENa or more negative than EK. So we set up a vertical voltage axis, and mark these two potentials on it. These voltages will be essentially fixed provided the cells are in good condition, because the concentrations are fixed, the temperature is fixed, and so are the other bits in the Nernst equation – k, e are universal physical constants. So these are like two rigid boundaries, and the actual voltage V at any moment must lie somewhere between them. What the Goldman equation is saying is that V behaves as if it were under the influence of two forces: PK pulls it towards EK, and PNa towards ENa: where it ends up depends simply on the balance between the two. In other words, changes in permeability cause changes in potential.

 |
Chloride
Haven’t we forgotten chloride? In our simple model, we assumed that chloride ions were unable to diffuse across, so we were justified in omitting them from the constant field
equation. But experiments show that real nerve and muscle membranes have significant chloride permeabilities, and it is obvious from the data that have been presented that there is a considerable imbalance in the concentrations of Cl– on each side. Nevertheless, there are two reasons why this ion can, for the moment, be safely neglected. The first is that in practice the Nernst potential for chloride is usually very close to the equilibrium potential of the nerve membrane, so that changes in its permeability have negligible effects on the resting potential. What happens is that potassium and chloride are free to move together as KCl until the Nernst potentials for both chloride and potassium are equal: that is, until [K]out/[K]in = [Cl]in/[Cl]out. Because internal [Cl] is so very much smaller than [K], a shift of a given quantity of KCI has an enormously greater effect on the chloride ratio than on the potassium (since the external concentrations remain essentially unchanged). Thus chloride adjusts itself to a resting potential that is essentially determined by potassium. Second, it turns out that during the action potential no significant alterations in chloride permeability occur; as we shall see, this is in sharp contrast to what happens to sodium and potassium. However, when, in Chapter 3, we look at synaptic mechanisms, we shall find that there are certain occasions when chloride cannot be neglected at all, and indeed most inhibitory synapses actually work through changes in chloride permeability.
equation. But experiments show that real nerve and muscle membranes have significant chloride permeabilities, and it is obvious from the data that have been presented that there is a considerable imbalance in the concentrations of Cl– on each side. Nevertheless, there are two reasons why this ion can, for the moment, be safely neglected. The first is that in practice the Nernst potential for chloride is usually very close to the equilibrium potential of the nerve membrane, so that changes in its permeability have negligible effects on the resting potential. What happens is that potassium and chloride are free to move together as KCl until the Nernst potentials for both chloride and potassium are equal: that is, until [K]out/[K]in = [Cl]in/[Cl]out. Because internal [Cl] is so very much smaller than [K], a shift of a given quantity of KCI has an enormously greater effect on the chloride ratio than on the potassium (since the external concentrations remain essentially unchanged). Thus chloride adjusts itself to a resting potential that is essentially determined by potassium. Second, it turns out that during the action potential no significant alterations in chloride permeability occur; as we shall see, this is in sharp contrast to what happens to sodium and potassium. However, when, in Chapter 3, we look at synaptic mechanisms, we shall find that there are certain occasions when chloride cannot be neglected at all, and indeed most inhibitory synapses actually work through changes in chloride permeability.
The resting potential
With Goldman safely behind us we are now in a position to understand why the resting potential is close to EK but not actually at it. The reason is that although at rest the permeability for potassium is much higher than for sodium, sodium permeability is not in fact zero: the ratio of the permeabilities is about 100:1, in frog muscle, at least. As a result, the resting potential is pulled a little more positive than would be expected for potassium alone, and the Goldman equation gives a pretty accurate prediction of the resting potential.
In fact, we can predict a lot more than that. If the equation is correct, then we should be able to predict V not just under resting conditions, but also when we deliberately mess about with the ionic concentrations. For example, we could alter the concentration of potassium in the external fluid: from the Nernst equation you can see that this will have the effect of altering the value of EK.
In a classic experiment, Hodgkin and Horowicz did exactly this. They bathed a frog muscle cell in solutions with different concentrations of potassium, and measured the resultant resting potentials. Now if the membrane had been only permeable to potassium, then it would have obeyed the Nernst equation, and the potential would be proportional to the log of the concentration outside. So plotting potential against the log of the concentration ratio would have given a straight line. For large concentrations, this nearly worked, but as the concentration was lowered, the results increasingly deviated from the straight line. But by using the Goldman equation instead of the Nernst, and feeding in a ratio of about 100 for the permeabilities of potassium and sodium, the prediction (blue line) was almost perfect.
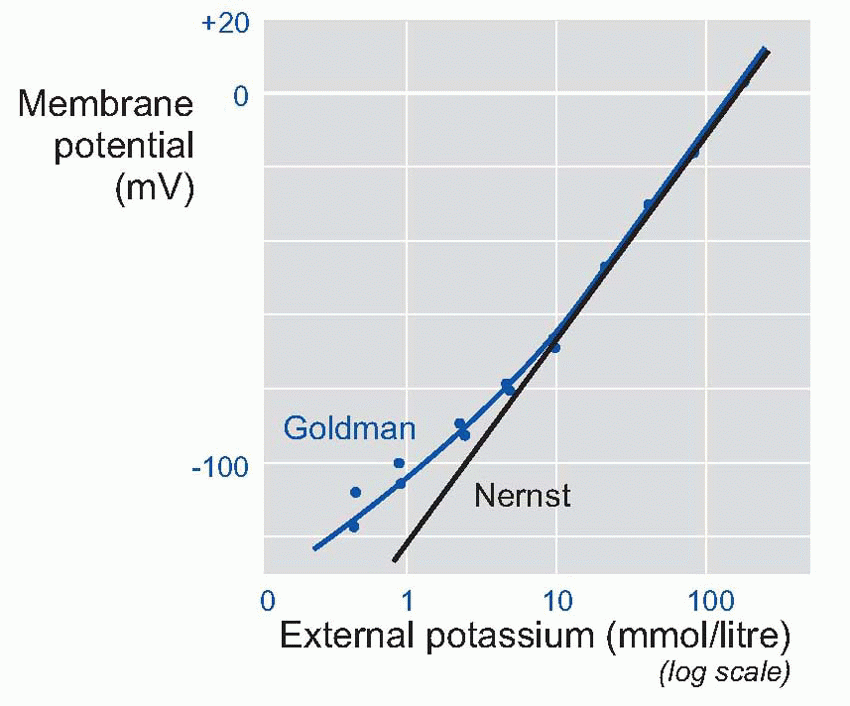 |
Similar experiments have been done on the giant axons of squids, creatures that have in fact played a surprisingly large part in the discovery of how nerves function. The reason is that despite enjoying a scary abundance of arms, squids are shy, timid creatures: when alarmed, they contract their mantle to force water out of their siphon, propelling themselves backwards. These are very rapid responses, and need very fast conduction, using a special extra large fibre innervating the mantle, called a giant fibre. ‘Giant’ here has rather specialized meaning (somewhere between 0.1 and 1 mm across); but they are big enough that one can put glass tubes down them. This in turn means that one can do two things: one is to measure the electrical potential, for instance during an action potential; the other is to sample the cytoplasm inside (axoplasm) and see what it’s made of. Indeed it is possible to squeeze their axoplasm out with a kind of miniature garden roller, and replace it with fluids of different composition, thus altering the potassium concentration inside as well as outside.
 |
The action potential
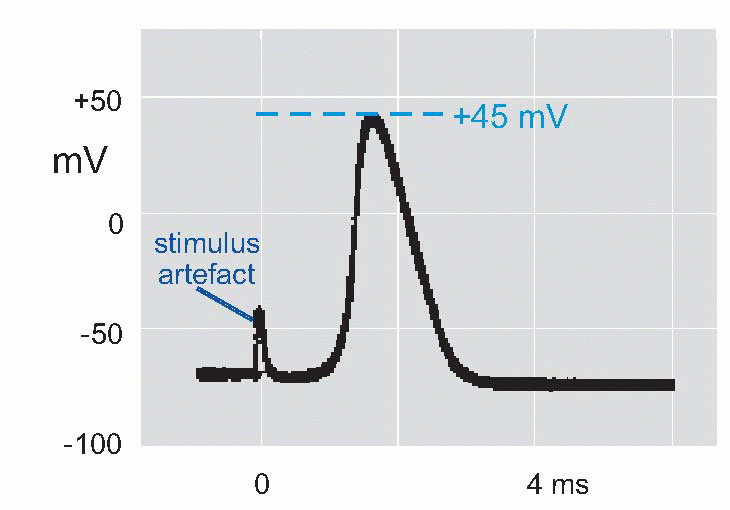
Now if we put a microelectrode inside a muscle fibre or squid axon, and stimulate it to get an action potential, we find that the potential of the inside relative to the outside
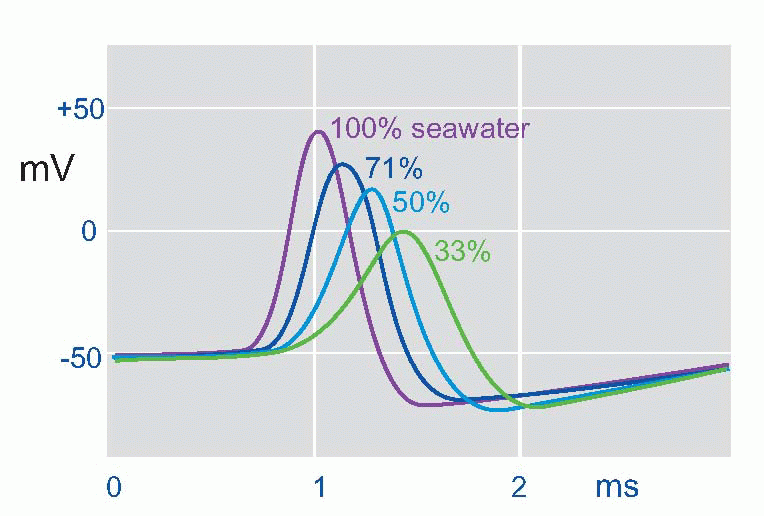
suddenly reverses from its resting -50 mV (in the squid) to a peak of some +40 mV, and then rapidly declines back to the resting potential again. This is the action potential or AP. (It is actually a monophasic action potential. You can also record action potentials with big electrodes outside the nerve fibre, and these are called biphasic action potentials. Box 2.1 explains the difference.) What sort of permeability change could account for this? Not just a simple shortcircuit, because then the potential would only tend towards zero, not reverse and become positive. In the squid the peak of the action potential is not far off at some +45 mV, strongly suggesting that a sudden increase in Na permeability pulls the membrane potential temporarily towards ENa(around +55 mV). By experimenting with various concentrations of sodium ions inside and outside the axon it was possible to demonstrate directly that the peak of the action potential was indeed dependent on ENa. If the concentration of external sodium was altered, by diluting the seawater with isotonic dextrose, although the resting potential didn’t vary – or only very little – what did alter was the height of the action potential: the lower the external sodium concentration, the smaller the action potential until eventually it is abolished altogether. Another test was to change the sodium not outside but inside, an experiment that is only feasible with the squid axon because of its huge diameter. Once again, alteration of sodium altered the size of the action potential, but the other way round: the smaller internal Na, the bigger the AP. The peak of the action potential therefore depended critically on the ratio of [Na]out/[Na]in, in other words, on the Nernst potential for sodium. So the natural explanation was that the action potential was caused by a brief increase in PNa, driving the membrane potential towards ENa.
suddenly reverses from its resting -50 mV (in the squid) to a peak of some +40 mV, and then rapidly declines back to the resting potential again. This is the action potential or AP. (It is actually a monophasic action potential. You can also record action potentials with big electrodes outside the nerve fibre, and these are called biphasic action potentials. Box 2.1 explains the difference.) What sort of permeability change could account for this? Not just a simple shortcircuit, because then the potential would only tend towards zero, not reverse and become positive. In the squid the peak of the action potential is not far off at some +45 mV, strongly suggesting that a sudden increase in Na permeability pulls the membrane potential temporarily towards ENa(around +55 mV). By experimenting with various concentrations of sodium ions inside and outside the axon it was possible to demonstrate directly that the peak of the action potential was indeed dependent on ENa. If the concentration of external sodium was altered, by diluting the seawater with isotonic dextrose, although the resting potential didn’t vary – or only very little – what did alter was the height of the action potential: the lower the external sodium concentration, the smaller the action potential until eventually it is abolished altogether. Another test was to change the sodium not outside but inside, an experiment that is only feasible with the squid axon because of its huge diameter. Once again, alteration of sodium altered the size of the action potential, but the other way round: the smaller internal Na, the bigger the AP. The peak of the action potential therefore depended critically on the ratio of [Na]out/[Na]in, in other words, on the Nernst potential for sodium. So the natural explanation was that the action potential was caused by a brief increase in PNa, driving the membrane potential towards ENa.
 |
 |
So it looked as if there was an increase of PNa at the start of the action potential, but what was setting it off? One attractive idea was that the depolarization of the membrane by local currents from the previous bit of nerve membrane might actually cause the increase in PNa. This would work beautifully, because there would then be positive feedback – depolarization increases PNa, which in turn causes more depolarization – which would have exactly the kind of explosive regenerative effects that were needed.
 |
So at this stage, of the three pieces of the puzzle (local currents, the effect of permeability on voltage, the effect of voltage on permeability) the first two were well understood – simple physics and the Goldman equation – but the third was a complete mystery. It was Alan Hodgkin and Andrew Huxley in Cambridge who set about trying to complete the puzzle by identifying the nature of this mysterious third process. 

How ionic permeabilities depend on potential
At first sight, the problem looks easy enough: what we want to know is how the permeability changes if the nerve fibre is depolarized. So why not simply use a micro-electrode to pass different currents through the membrane, to set up different membrane potentials V, and see what happens to its conductance, g? We can work out g very easily: conductance is simply the inverse of resistance: resistance is V/I, so g is I/V – the current divided by the voltage. And we can assume that g is in turn simply proportional to the sum of all the permeabilities.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








