Fig. 8.1
Schematic representation of cerebellar circuits. At the sub-cortical levels, afferent fibers carrying sensory information activate the deep cerebellar nuclei and inferior olive cells. In the cerebellar cortex, there are granule cells, Golgi cells, Purkinje cells, stellate cells, basket cells, Lugaro cells and unipolar brush cells. The granular layer (in this work) is a feed-forward excitatory network with several inhibitory loops; the main inputs to granule cells come from mossy fibers that diverge from deep cerebellar nuclei. Golgi cells provide inhibitory inputs to granule cells and granule cell ascending axons form parallel fibers that activate the Purkinje cells. The cerebellum and its circuits are arranged as modules, microzones and multizonal complexes [89]
Granular layer is hypothesized to perform recording of the MF inputs into a sparse representation that permits noise reduction by lateral inhibition [20], generated by Golgi cell. Due to the limited set of combinations of MF excitatory and GoC inhibitory inputs, there are a discrete number of synaptic connections for studying the relationship between input and output in the MF-GrC relay.
Long-term changes in synaptic strength named as synaptic plasticity is one of the important neurochemical foundations of learning and memory [21, 22]. Introduced by Donald Hebb in 1949, spike time dependent plasticity is supposed to provide the cellular basis for learning and memory and takes the form of either Long Term Potentiation (LTP) or Long Term Depression (LTD) [1, 23]. A high frequency signal (typically 100 Hz) induces a strong glutamate release into the synapse and depolarizes the postsynaptic neuron [24]. The depolarization induced by successive excitatory postsynaptic potentials (EPSPs) overlap and cumulatively produces action potentials or spikes. Amount of neurotransmitters released into the synaptic cleft activates postsynaptic receptors to elicit a postsynaptic response. In the cerebellum granular layer, induction of LTP at MF-GrC synapses enhances the spike train response of GrCs [25]. During MF- GrC LTP, there is an enhancement in neurotransmitter release and intrinsic excitability of GrC [25, 26]. LTD expression was associated with a decrease in release probability of the mossy fiber, showing changes opposite to those characterizing LTP [27]. Therefore induction of plasticity by changing the intrinsic excitability of the GrC and excitatory release probability of MF [23, 26] at MF-GrC synapses changes the spike/EPSP train response of GrC [17].
At the cellular scale, single-neurons process information mainly through spikes or action potentials [28]. The mechanisms involving the responses produced by the granular layer implicates changes in release probability and intrinsic excitability over mossy fiber-granule cell relay [29–31].
Granule Neuron
Granule cell is one of the most numerous of neurons in the cerebellar cortex [32, 33]. The soma in the rat cerebellum is spherical and is usually of ~ 5 μm in diameter [34]. The cells have 3–5 dendrites on an average and are about ~ 13 μm in length. The axon is usually very thin ~ 0.1 μm has two known components, ascending axon which then extends as the parallel fiber [35, 36]. The axon starts from the granular layer and extends into the molecular layer. The granule neuron is one of the best known neurons where the biophysical properties have been characterized extensively and modelled using both detailed and simple compartmental models [13, 32, 34, 36, 37].
Cerebellar granule cells have been known to recode information coming from the mossy fibers via expansion recoding due to large convergence-divergence ratio [13, 38, 39]. Because of the location, such cells are considered critical since all operations of cerebellum depend on the elaboration of incoming sensory and tactile signals into the cerebellum. The connectivity with the granular layer, makes granular layer signal recoding unique. Each granule cell dendrite receives an input from a different mossy fiber and an inhibitory synapse from a Golgi cell. The granule cell dendrites also form a specialized structure called glomerulus, where the postsynaptic densities are observed [40, 41]. The glomeruli act as microenvironments for neurotransmitter related mechanisms.
Golgi Neuron
Golgi cells are inhibitory interneurons of the cerebellar granular layer, which receive inputs from Mossy fibers and respond to afferent stimulation in vivo with a burst-pause sequence interrupting their irregular background low-frequency firing [42–44]. Golgi neurons show fastest transient in soma, intermediate in dendrites and slowest in axon [43]. Golgi cells are known to inhibit granule neurons via two loops [45, 46].
Methods
We have used NEURON [47] as the modelling tool. The study carried out in this paper involved the use of computational models of neurons based on experimental data from p19-23 Wistar rat cerebellum [33, 43]. Mathematical neuron models of granule cell [33, 48], and Golgi cell model [43, 44] were used in this network study. Modeling reliability for spiking models was based on the extensive characterization of membrane currents and the compact electrotonic structure of cerebellar granule cells [33, 34]. The models used AMPA (2-amino-3-(5-methyl-3-oxo-1,2- oxazol-4-yl) propanoic acid) and NMDA(N-Methyl-D-aspartate) receptor components as excitatory MF-GrC synapses and GABA (γ-Aminobutyric acid)-ergic synapses for the Golgi cell- GrC relay [33]. On an average, each granule cell receives excitatory connections from 4 to 5 mossy fibers [25, 33, 34].
Multi-Compartmental Granule Neuron Model
Detailed multi-compartmental granule cell (GrC) model [33] was used and simulations included responses by varying the excitatory (E) and inhibitory (I) synaptic inputs. The model of the granule cell was based on multi-compartmental cable theory and included soma, axon, hillock and dendritic compartments. The model consisted of 52 active compartments connected to each other via the 3/2-power law [18]. For each of the compartments, membrane voltage Vm had to be estimated separately.
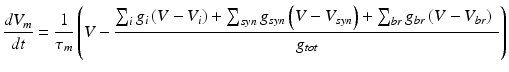
Where g is the conductance corresponding to i (ion channel), syn (synaptic dynamics), br (neighbouring attached branch) and tot (total). Here τ_m = R_mC_m which is the time constant of oscillation of the membrane based on its membrane resistance, R_m and membrane capacitance, C_m. The calcium current in the model was included as
![$$\frac{d~[Ca]}{dt}=-\frac{{{I}_{Ca}}}{\left( 2F.A.d \right)}-\left( {{\beta }_{Ca}}\left( \left[ Ca \right]-{{[Ca]}_{O}} \right) \right)$$](/wp-content/uploads/2016/12/A319630_1_En_8_Chapter_Equb.gif)
where d is the depth of a shell adjacent to the cell surface of area A, β_Ca determines the loss of calcium ions from the shell approximating the effect of fluxes, ionic pumps, diffusion, and buffers, ![$$ {\left[\mathit{C}\mathit{a}\right]}_{\mathit{O}}$$](/wp-content/uploads/2016/12/A319630_1_En_8_Chapter_IEq1.gif)
![$${{[Ca]}_{o}}$$](/wp-content/uploads/2016/12/A319630_1_En_8_Chapter_IEq2.gif) is resting [Ca] and F is the Faraday’s constant. [Ca] is the calcium channel dynamics as reported in [33].
is resting [Ca] and F is the Faraday’s constant. [Ca] is the calcium channel dynamics as reported in [33].
![$$ {\left[\mathit{C}\mathit{a}\right]}_{\mathit{O}}$$](/wp-content/uploads/2016/12/A319630_1_En_8_Chapter_IEq1.gif)
![$${{[Ca]}_{o}}$$](/wp-content/uploads/2016/12/A319630_1_En_8_Chapter_IEq2.gif) is resting [Ca] and F is the Faraday’s constant. [Ca] is the calcium channel dynamics as reported in [33].
is resting [Ca] and F is the Faraday’s constant. [Ca] is the calcium channel dynamics as reported in [33].Granule Cell Synapses
The model GrC has 1–4 excitatory (one for each dendrite) and 0(no inhibition)–4 inhibitory connections (one for each dendrite) [33]. The detailed explanations of ionic channel dynamics, compartmental localization of ion channels and electrotonic structure of this granule neuron model are described elsewhere [25, 33, 34]. Since granule cell is one of the rarest neurons where the ionic channel densities can be accurately determined using whole-cell patch clamp, the ion channel dynamics that were modelled previously [33–35] and is not repeated here. Also, excitatory and inhibitory synaptic inputs to the dendrites were located in dendritic tips, although in neighbouring dendritic compartments. Presynaptic dynamics for the MF-GrC was modelled separately as in [25, 33] due to components such as facilitation and depression.
Excitatory post-synaptic mechanisms were shown as AMPA and NMDA postsynaptic receptor components as seen in granule neurons. AMPA receptor dynamics was modelled using a three-state scheme and a 2D diffusion model whereas the NMDA receptors used Boltzmann equation as seen in [49]. Both the excitatory pre-synaptic and excitatory post-synaptic mechanisms are described in detail elsewhere [25, 37]. The GoC-GrC inhibitory synapse model was based on the following presynaptic dynamics: release probability = 0.35, τREC = 36 ms, τfacil = 58.5 ms and τI = 0.1 ms, respectively and as described in [50], Effects of blocking inhibition by adding gabazine were also simulated by setting GABAergic conductance in inhibitory fibers to zero.
Golgi Cell Model
The Golgi cell model (GoC) was adapted from [43]. The model produced responses that was used to drive the inhibitory connections onto the granule cell via the Golgi cell-Granule neuron feed-forward circuit.
Granule Layer Circuitry
Mossy fibers activate granule neuron via AMPA and NMDA receptors at the post-synaptic site [25, 33]. Mossy fiber also activated Golgi cells with a divergence ration of 1:3.6 [13]. In most of our circuit models, we ignored the feedback loop from granule cells to Golgi cells since that circuit takes part at a later stage of the post-synaptic response and was not characteristic of the models in this study.
Mutant Neuron Models
To model mutant models, we adapted the sodium channel related intrinsic excitability [35, 36] and synaptic dysfunctions [51, 52] as seen during certain disorders. The sodium channel used in control and mutant models was a 13-state, allosteric sodium channel model with values as described elsewhere [35]. For the synaptic sparseness, we selectively disabled NR2A-related NMDA receptors and reconstructed the synaptic response as indicated.
Center-Surround Excitation
Stimulating mossy fibers with an electrode at a particular point activates granule cells in the network in a center-surround activation pattern [53]. Within a ‘spot’, cells which are in close proximity to the electrode will receive high excitation and the periphery layer cells receive less excitation. Our model of the granular network shows the pattern activated as a ‘spot’. The center-surround pattern showing the decreasing strengths of excitation can be noticed from the center to the periphery.
Simulating LTP-LTD
By modifying intrinsic excitability and release probability [25, 54], we simulated plasticity in the granule cells. We modified intrinsic excitability by changing ionic current density or gating. We modified the on-off gating characteristics of sodium channel to modify sodium activation and inactivation parameters [36] for higher and lower intrinsic excitability. Combining intrinsic excitability and varying release probability of synapses we were able to model long-term potentiation (LTP) and long-term depression (LTD) for simulating spike-time dependent plasticity (STDP) in the MF-GrC synapses.
Local Field Potential Reconstruction
Network local field potentials (LFP) was reconstructed using techniques based on convolution of jittered single extracellular potentials [36] and by linear summation of compartmental components [12]. In both methods, NEURON’s extracellular mechanism [47] was used for calculating membrane ionic currents from the compartments. The network model consists of 1382 Multi-compartmental granule cells, 5 Golgi cell, 88 Mossy fibers rosettes (MF) and 16,500 synapses arranged in 35 μm cubic slice of cerebellar cortex model. Convergence and divergence ratios used to build the network model were based on earlier studies [39, 55].
Artificial Spiking Neuron Models
We also employed another group of models for their simplicity in reproducing known neuronal behaviour patterns, namely, the artificial spiking models. These models are computationally inexpensive and can be used to simulate large scale network models with relatively less time. There are many existing spiking models starting from leak integrate-and-fire models to modified versions of spike response model. Simplified spiking models depend on two equations, one regulating the membrane potential and the other regulating the adaptation or subthreshold dynamics. The membrane potential will rise till threshold and then exponential mechanism triggers rapid rise and resets back to the resting potential. We used the adaptive exponential integrate and fire model [56] which is well known to replicate realistic neuronal firing patterns. This model replaces strict threshold with more realistic smooth threshold [57] as observed in exponential integrate and fire neuron [58].
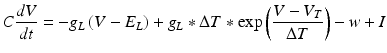
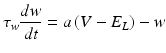
Where ‘C’ is the membrane capacitance, ‘gL’ is leak conductance, El is the resting potential, ‘ΔT’ is the slope factor and ‘VT’ is the threshold potential. Variable ‘w’ determines the level of adaptation of the neuron and ‘a’ modifies sub-threshold adaptation [57]. Exponential term determines the early activation of voltage-gated sodium channels in the model (Table 8.1).
Table 8.1
AdEx parameter values used for modeling neuronal firing
C (pF) | gL (nS) | EL (mV) | ΔT (mV) | VT (mV) | I (pA) | VR (mV) | a (nS) | b (pA) | τw (ms) | |
|---|---|---|---|---|---|---|---|---|---|---|
DCN | 200 | 10 | − 70 | 2 | − 50 | 0 | − 58 | − 20 | 675 | 8 |
IO | 350 | 10 | − 65 | 2 | − 50 | 0 | − 58 | − 13 | 1200 | 1 |
Golgi cell | 511 | 13.1 | − 58 | 7 | − 60 | 0 | − 50 | − 20 | 1033 | 14.65 |
Purkinje cell | 100 | 10 | − 65 | 2 | − 50 | 0 | − 58 | − 13 | 260 | 1 |
Granule cell | 1 | 10 | − 70 | 2 | − 50 | 20 | − 58 | − 10 | 265 | 0.71 |
Using spiking neuron models, we reproduced different neuronal firing patterns as observed in rat cerebellum specifically those of deep cerebellar nuclei (DCN), inferior olivary nucleus (IO), Golgi cell, Purkinje cell and granule cell (see Table 8.1).
Validating In Vitro and In Vivo Behavior
In vitro like behaviors were studied in the granule cells by giving single spike as input via MF terminals. In vivo like behaviors were characterized by short bursts (5 spikes per burst). First EPSP/spike latency was measured from the time of input stimulus to time of the peak of the output EPSP/spike. In plots latency is indicated synonymously as occurrence times of spike/EPSP. The excitatory stimulus was applied at t = 20 ms and inhibitory stimulus at t = 24 ms. The EPSP/spike amplitude was measured from the resting voltage of − 70 mV to the voltage of the peak of the EPSP/spike generated. In vivo GrCs tend to discharge bursts in vivo [60] whereas in vitro GrCs produced spikes or doublets with high excitation and EPSPs with lower excitation [63].
Results
Granule Cell Post-Synaptic Responses
Using a mathematical model, we explored the role of EPSPs as a major information carrying component in addition to spikes. Most studies consider spikes as the major information carrying component in neurons. Studying both spikes and EPSPs and how EPSP-spike complex modulate information encoding in single neurons can possibly reveal the importance of the large number of granule neurons in the cerebellum and how sparse recoding happens in the cerebellar input layer.
Variation in number of synaptic inputs affected both types of post-synaptic responses in granule neurons. Typically excitation with minimum number of inputs generates excitatory post-synaptic potentials (EPSPs) while larger number of inputs causes spikes. Granule neuron model [33], under control condition in vitro with one or two active mossy fiber (MF) inputs generated EPSPs. Three excitatory synaptic inputs generated spikes and four inputs generated spike doublets (Fig. 8.2a). In vivo synaptic inputs generated more spikes (Fig. 8.2b) due to burst-like inputs in MFs.
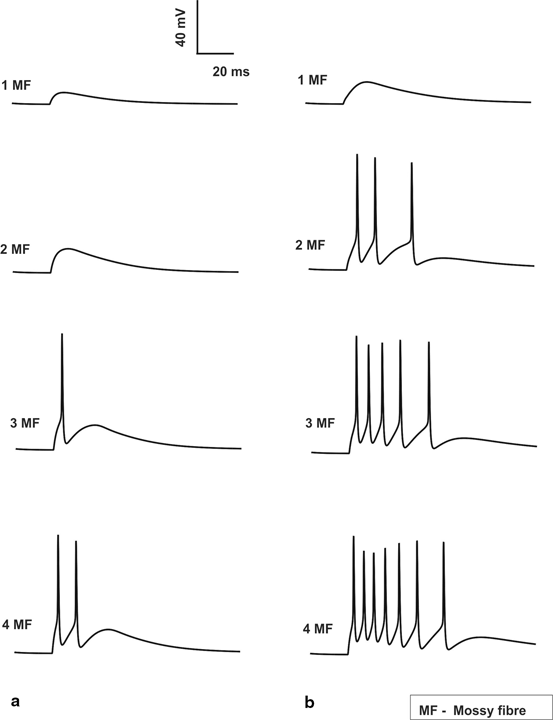
Fig. 8.2
Spiking properties of granule cell. a In vitro Granule cell shows spikes only if 3 MF inputs are activated which elicits a single spike and when all 4 MF inputs are activated a doublet is seen. No inhibitory inputs are provided to the cell. b In vivo Granule cell without inhibition gives 3, 5 and 7 spikes for 2, 3 and 4 MF activation
The EPSPs and spikes generated were found to be sensitive to the inhibitory- excitatory balance of the MF-GrC relay. Increase in MF excitatory inputs tend to reduce the number of EPSPs generated while it increased the number of spikes generated. When inhibition was included, EPSPs tend to increase but the spiking activity of the GrC decreased (see Fig. 8.3, EPSPs are not seen due to in vivo like inputs along MF). Single mossy fiber input combined without or with inhibitory connections always generated zero spikes but produced EPSPs.
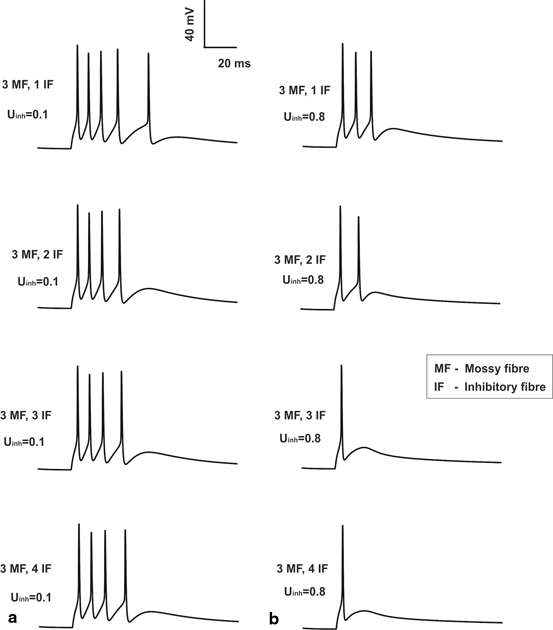
Fig. 8.3
Feed forward inhibition and granule cell. a Granule cell having with low inhibition (low release probability on inhibitory synapses). b Granule cell firing with high inhibition (high release probability on inhibitory synapses). For comparison sake, the number of MF inputs is set to three and the release probability of excitatory synapses was set at control (0.416) value. One can note from top (1 inhibitory fiber input) to bottom (4 inhibitory inputs) varying inhibitory synaptic inputs are applied
Over all possible combinations of excitation (E) and inhibition (I) i.e. summing all responses for combinations I0E1, I0E2 etc. until I4E4 generated an estimate of the maximum possible EPSPs and Spikes over all possible release probabilities (See Fig. 8.4).
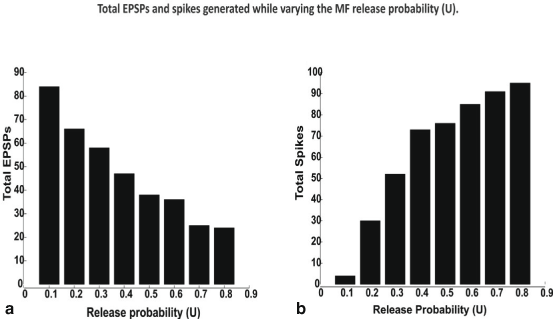
Fig. 8.4
Total EPSPs a and spikes, b generated while varying the MF release probability. All spikes and EPSPs for all possible combinations of excitatory (E) and inhibitory (I) synaptic inputs such I0E1 to I4E4 were summed to estimate total spikes. In vivo like inputs—bursts along MF were simulated. Input bursts favored spikes due to temporal summation of inputs facilitated by NMDA channels
Varying MF Release Probabilities Affect Spike-EPSP Ratio
To understand whether increase in release probability could determine changes in EPSP, the release probability (U) of excitatory synapse was modified from control (U = 0.416) [25] while the release probability of inhibitory fiber was set at its control value (Uinh = 0.34) [59]. Various synaptic activation patterns were applied as inputs via MF and for each of the activation patterns, number of spikes; first spike latency (from the peak of the spike) and amplitude of the initial spike were measured. Here, EPSPs were measured from the initial membrane potential of − 70 mV. With inputs from 4 MF excitatory synapses and 2 inhibitory synapses (see Fig. 8.5a) single spike was observed and the spike measured 15.52 mV at 23.225 ms under control condition (U = 0.416).
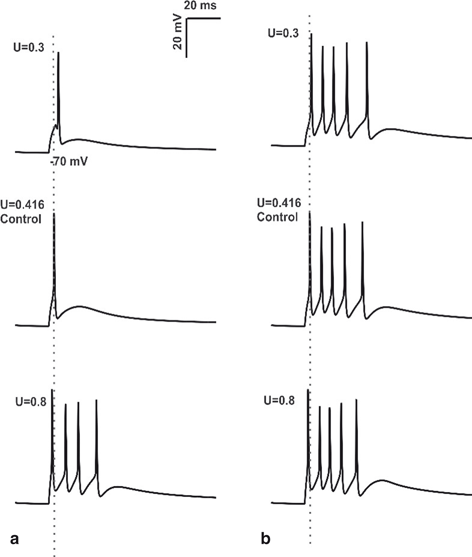
Fig. 8.5
Changes in Mossy Fiber release probability. a Spike response obtained using in vitro like input through 4 MF synapses, 2 inhibitory synapses of granule cell with varying release probability. First spike latency was reduced (see the grey dotted line) and number of spikes was increased by the increase in release probability. b 4 MF synapses, 2 inhibitory synapses activation of granule cell in vivo with changes in release probability (U). At U = 0.3, change in initial spike delay and decrease in number of spikes was clearly observed. During control condition (U = 0.416), increase in number of spikes and shortening of first spike latency was seen (the grey dotted line passing through the center of first spike). When the release probability of excitatory synapses was increased to 0.8, number of spikes remains constant, small change in initial spike latency was seen
When release probabilities of the excitatory synapses were increased above 0.416, number of spikes increased, spike amplitude increased and the first spike latency decreased. A decrease in number of spikes was observed when the release probability of excitatory synapse was decreased below 0.416. First spike latency decreased and amplitude increases in all cases (see Fig. 8.6a). The same protocol was repeated with other activation patterns (data not shown) comprising combination of excitatory and inhibitory synapses. In vitro model behavior with increased release probability of excitatory synapse was associated with decreased first spike latency, increase in amplitude and increase in number of spikes.
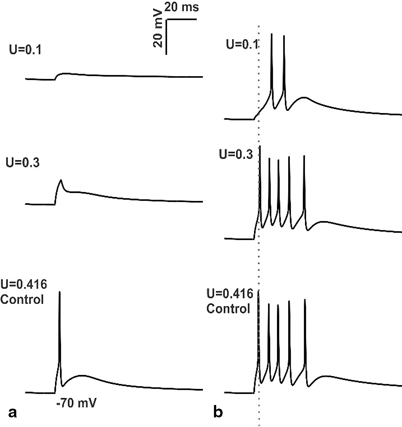
Fig. 8.6
Simulations of changes in mossy fiber release probability and intrinsic excitability. a In vitro behavior of granule cell model with low release probabilities of MF synapses b In vivo behavior of granule cell model during low release probability of mossy fiber. First spike latency was increased when there was a reduction in MF synapse release probability coupled with low intrinsic excitability of granule cell (see grey dotted line passing through control). It can be noted that the decrease in release probability of MF synapses was associated with decrease in number of spikes
GrCs tend to discharge bursts in vivo [60]. With input combination of 4MF synapses and 2 inhibitory synapses, in vivo model showed 5 spikes, the timing and amplitude of initial spike was 15.55 mV and 23.15 ms respectively under control condition (U = 0.416). The release probability of MF synapse was first reduced and then increased from the control condition to study how the changes in release probability of MF synapse affects granule cell firing in vivo (Fig. 8.5b). At U = 0.1 release probability the GrC model showed 2 spikes with initial spike amplitude and timing as 9.28 mV and 31.775 ms respectively. Release probability of the excitatory synapse was increased to 0.3, 5 spikes were observed, amplitude and first spike latency measured 14.82 mV and 24 ms respectively. With increase in release probability above 0.416 (control), number of spikes remained unchanged (at 5 spikes), but small changes in spike amplitude and spike timing was observed (see Table II in [61]). In vivo model with the reduction in release probability of MF synapses below 0.416 (control) was associated with decrease in number of spikes, decrease in spike amplitude and increase in first spike latency. When the release probability was increased above the control (U = 0.416), number of spikes remained unchanged and small changes in spike amplitude and spike latency were observed.
Varying MF release probabilities and measuring the EPSP-spike response for the different excitatory- inhibitory input combinations in vivo involving an increased MF release probability decreased the number of EPSPs and increased spiking (Fig. 8.4a, b), as expected. The percentage of EPSPs generated during LTD was 67.5 % while during LTP was 32.5 %. The percentage of spikes produced during LTP was 31.4 % while during LTD was 68.6 %. The increase—decrease pattern of EPSP –spike coupling was found to follow a seemingly symmetric behavior. Release probability change affected GrC firing only if a favorable excitatory—inhibitory balance was maintained in the cell (data not shown). The simulations suggest that in vivo, spikes were more common than EPSPs. A full estimate of the EPSP-Spike counts during control, LTP and LTD is shown in Fig. 8.7. The contributions with MF release probabilities between EPSPs and spikes in the EPSP-spike complex were not linear (as indicated by total numbers in Fig. 8.4).
A study on the effects of varying of inhibitory release probabilities on granule neuron firing was performed (see Fig. 8.3). Spike amplitude was changed significantly when the release probability of inhibitory synapse was increased from 0.1 to 0.8, but the number of spikes and timing was preserved. Spike amplitude was decreased for both increases in number of inhibitory inputs as well as the release probability of inhibitory synapses during in vitro simulations. In vivo behavior of granule cell model indicated the increase or decrease in release probability of inhibitory synapse did not affect the timing of granule cell firing due to delayed inhibition. However, decreased release probability of inhibitory synapses resulted in increased number of spikes, but there was no effect on amplitude or latency.
Predicting the Effects of LTD
Plasticity in MF-GrC has been known to be bidirectional [23]. The expression of LTD was associated with decrease in release probability of the excitatory synapses, thereby showing directionally opposite characteristics of LTP [27]. LTD arises due to weak, asynchronous, sporadic activity in pre and postsynaptic neurons [54]. To test effects of LTD induction, intrinsic excitability of the model was reduced and the release probability of MF synapses was reduced below 0.416(control) and its effect in granule cell firing was observed for various synaptic activation patterns. The release probability of inhibitory synapse was kept constant (Uinh = 0.34).
With low release probability of MF synapses (U = 0.1) in vitro granule cell model with low intrinsic excitability did not produce spikes (see Fig. 8.6a). In the presence of low levels of inhibition (0 or 1 inhibitory synapses), and during co-activation of 4 MF synapses, the model produced single spike at U = 0.3 release probability. The effect of low release probability of MF synapses and low intrinsic excitability of in vivo granule cell was simulated and studied.
When the release probability of MF synapse was increased to 0.3, (U = 0.3) number of spikes was increased to 5, first spike latency was decreased while amplitude was increased (Fig. 6b, also see Table V in [61]). In vivo like inputs to granule cell model under control condition produced 5 spikes and the initial spike measured 15.55 mV at 23.125 ms.
Low intrinsic excitability of granule cell affected spike amplitude and first spike latency, but it did not show significant effect on number of spikes (see [61]). Decrease in release probability of MF synapses affects spike latency, number of spikes and spike amplitude. MF-GrC LTD was associated with decrease in spike amplitude and increase in first spike latency.
Selective Inhibition and Spiking During Plasticity
Inhibition had modulatory effect on granule cell spiking. Spike amplitude was changed significantly when the release probability of inhibitory synapse was increased from 0.1 to 0.8, even though number of spikes and timing was preserved (see Table VI in [61]). With increasing release probability in the inhibitory synapses, spike amplitude decreased. This was observed for various combinations of inhibitory and excitatory synapses.
For in vivo like inputs, amplitude and latency of the first spike remained unchanged (see Table VII in [61]). Golgi cells regulate the induction of long-term synaptic plasticity at the mossy fiber–granule cell synapse. The main output from Golgi cells to granule neurons is GABAergic and inhibits the granule cells [50]. The spike amplitude and first spike latency remained constant for all release probabilities of inhibitory synapses for any particular combination of excitatory-inhibitory synapses. Inhibition did not affect first spike latency or spike amplitude during burst like in vivo inputs along MF (see Fig. 7b). For single spike (as seen in vitro) inputs along excitatory and inhibitory synapses, varying inhibition (both number of active inhibitory synapses and varying inhibitory release probabilities) regulated spike amplitude (see Fig. 7a).
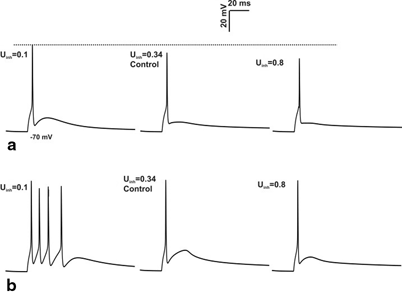
Fig. 8.7
Effect of inhibition on spike amplitude. a 4 inhibitory synapses, 3 excitatory synapses activation of granule cell with varying the release probability of inhibitory synapse for single spike input. Increase in the release probability of inhibitory synapse cause the reduction in spike amplitude (see the grey dotted line). b Response produced by burst-like input through 4 inhibitory synapses, 3 excitatory synapse in granule cell. In vivo behavior showed significant changes not in amplitude but in number of spikes
The simple spiking network models were used to abstract rate coding information and produced similar results (data not shown).
Local Field Potential Reveals Role of Single Neuronal Functions in Populations
Population signals of neural circuits reveal emergent behavior as patterns of information flow in the underlying neural circuits [12, 36, 62]. The role of precise timing between intracellular events in a single neuron and its encoding within population signals such as local field potentials has been explored with attention to understand the rate code correlation between neurons in such signals [63]. This attention to spike encoding is also because of information being encoded in noise [36, 64]. Local field potentials (LFPs) are recorded as waveforms of extracellular activity that arise from complex interactions of spatial distribution of current sources, temporal dynamics, spatial distribution of dipoles and underlying conductive properties of the extracellular medium [65, 66].
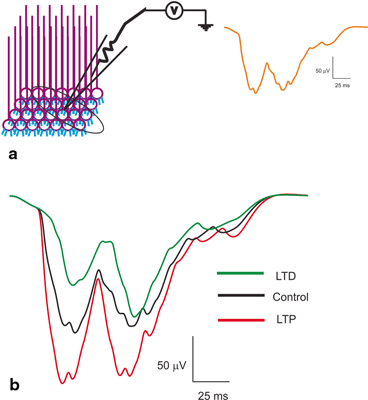
Fig. 8.8
Local Field Potential reconstructions. a Schematic of a LFP being recorded from a population of granule neurons. Orange trace on the right shows T-C wave generated as post-synaptic LFP for in vivo-like burst inputs. Two bursts through the granule neurons generate the T (short burst input) and C wave (long burst). b Induced plasticity reconstructions at the LFP level [36]. With induced plasticity, amplitude and lag varied compared to the control. Amplitude increased and lag decreased for LTP while lag increased and amplitude decreased for LTD
Local field potentials from experimental data are known to reflect the neural activity of the cells in the vicinity [12, 36, 67]. Granular layer LFP generated by tactile stimulation [23] was reproduced in the network model (see Fig. 8.8a) by giving short and long pulses through mossy fiber bundles [60, 68, 69]. The in vivo LFP was composed of ‘T’ and ‘C’ waves. The Trigeminal (T) wave corresponds to afferent inputs and the following cortical (C) wave is generated from cerebral cortex and pontine nuclei. In our network, the ‘T’ wave was generated by applying 5 spikes at 500 Hz along the mossy fiber synapse at 20 ms, and the ‘C’ wave was produced by 9 spikes at 500 Hz via mossy fiber synapse at 60 ms. The model was able to reconstruct population responses from the network model (see Fig. 8.8).
Spike-time dependent plasticity inductions were simulated by altering the intrinsic excitability and the synaptic release probability as mentioned in methods of [12, 36]. During induced LTP, simulations showed the LFP wave [23, 36] with an increased amplitude and width for both T and C waves compared to the control conditions (see Fig. 8.8b). With induced LTD–like conditions, the T and C wave of LFP showed a decreased amplitude and width compared to control (see Fig. 8.8b). Although modification of single neuron properties affected the spike propagation to continued inputs, varying such properties affected local field signals. The amplitude and lag variations of reconstructed post-synaptic LFP seems to be affected by the excitation pattern, synaptic variations and nature of stimulus [36].
Spatio-Temporal Dynamics are Characteristic of Network Geometry
Studies resolving single cell activity in multiple neuron responses have been indicating granule cells produced various spikes reflecting the variability of neurotransmission process [70, 71]. The pattern of excitation and role of inhibition elicited by delivering a single stimulus to white matter was reported using maps generated by voltage sensitive dye-based imaging [10]. Granular layer responses was regulated by inhibition [72]. To test the frequency-dependent transmission in granular layer, we reconstructed the map using 730 granule cells, 2 Golgi cells, 40 mossy fiber rosettes to pack 35 μm3 of cerebellar cortex (see Fig. 8.9).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree





