2.3 Hz) of PD is significantly higher [73]. Second, the symptom severity may be more relevant to the neuronal firing patterns than to the firing rates of GPi [4, 8, 9, 15, 38, 43, 47, 54, 56, 61, 66, 76, 82, 84]. In particular, numerous experimental studies have demonstrated that neurons within both STN and GPi show an increased level of bursting activity during parkinsonian state [4, 9, 47, 54, 61, 73]. Third, measuring synchronized activity across many neuronal elements of GPi using local field potential (LFP) recording [71] showed that the untreated PD is associated with an increased tendency to synchronization.
Since motor outputs from GPi target the anterior ventrolateral nucleus of the thalamus (VLa) [1, 17, 40, 50, 85], which serves to relay signals between cortical areas [22, 23, 24, 28], it has been hypothesized that pathological GPi outputs may induce parkinsonian signs by changing thalamic activity patterns [16, 30, 31, 49, 72], in particular, by compromising thalamocortical (TC) relay [11, 25, 26, 58, 67].
Drawback of Conventional DBS
The apparatus of the conventional DBS consists of (1) an electrode that is approximately 1.25 mm in diameter, (2) a stimulator including battery, and (3) an extension cord connecting the two. The conventional DBS delivers an ongoing stream of high frequency current pulses to the stimulation target. The electrode is placed into the stimulation target such as STN and GPi. In particular, both STN or GPi stimulation sites are commonly practiced for treating PD [33, 81, 82]. Deep brain stimulation has significant advantages compared with ablative surgery pallidotomy (destroy part of GPi) or thalamotomy (destroy part of thalamus). Considering DBS does not require making a destructive lesion in the brain, DBS is, in principle, reversible and does not preclude the use of possible future therapies in PD requiring integrity of the basal ganglia circuitry.
Although DBS has achieved remarkable success, it is desirable to improve DBS when considering some of its significant drawbacks:
“Dumb” stimulation [3]: The conventional DBS employs a stimulation with constant high frequency pulses that relies on external force determined by parameters such as type of stimulation (monopolar or bipolar), voltage, frequency (Hz), and pulse width (in ms). Such form of stimulation is considered “dumb” because the external force is not guided by the changes in the brain’s electrical activity relevant to the disorder being treated.
Laborious DBS parameter tuning: For a given patient, tuning the DBS parameters to gain optimal treatment efficacy for a given stage of the disease could be a laborious and difficult task, especially for those patients with movement disorders that would take months to see the therapeutic effect of DBS.
High energy cost and invasive surgery to replace the battery [2]: It requires surgery of opening chest wall to replace the battery of the pulse generator. The cost of applying chronic DBS for patients of some other movement disorders, such as dystonia, is even higher than those for PD patients due to the younger age of onset [80]. Hence, more frequent invasive surgeries for battery replacements is needed [41, 46]. If the stimulation can be energy efficient, the battery’s life will be prolonged, and fewer invasive surgeries are needed.
Computational Study of Conventional and Closed–Loop DBS
Multi–site Delayed Feedback Stimulation (MDFS) was first suggested as an alternative to the conventional DBS in [34, 35, 36, 64, 77]. In their MDFS protocol, the LFP of the stimulation target population is measured, filtered, delayed and fed back into the same ensemble through multiple stimulation sites that have different time delays. Compared with the conventional DBS, MDFS has at least two advantages. First, it is noticeably “smarter” in that it can be adjusted to brain’s own electrical signals, whereas the conventional DBS entirely relies on external forces. Second, the energy required to administer such stimulation can be maintained at lower level. Although these earlier works contributed toward an excellent idea, the outcomes of MDFS are limited by the choice of model and the focus of study.
Hauptmann et al. [34, 35, 36] used both non–biophysical phase models and the Morris–Lecar model to describe the activity of excitatory neurons. Other work by Rosenblum and collaborators [64, 77] used the Hindmarsh–Rose equations. Both phase models and the Hindmarsh–Rose model are not biophysical models. The Morris–Lecar model is a simplified 2–dimensional reduced model in which several of the ionic currents are not presented in the tracking of real membrane potential. These models are very limited in describing the neuronal behavior of the basal ganglia.
In [34, 35, 36, 64, 77], only one neuron population that is representative of the excitatory STN neurons in the basal ganglia were considered. The authors introduced local synaptic coupling among the excitatory neurons that is responsible for the synchronization of the stimulated population. In general, it is straightforward to induce synchronization by strong excitatory coupling; however, this synchronization mechanism is unfaithful to the anatomy of basal ganglia and the pathology of PD [32].
The computational work in [34, 35, 36, 64, 77] reported desynchronizing effect on abnormal synchrony of neuron ensembles. The stimulation neither breaks the bursting pattern nor reduces the burst rate which are important characteristics of GPi and STN activity in PD. None of the work in [34, 35, 36, 64, 77] incorporated any criteria to evaluate the downstream neuronal behavior in the thalamus that is relevant to the clinical effectiveness of MDFS.
Rubin and Terman’s (RT) Basal–Ganglia Thalamocortical Network Model
Rubin and Terman [66] laid the ground work on the theoretical analysis of DBS using a conductance–based network model of basal ganglia and thalamus. They set up the first Hodgkin–Huxley type of computational model including the important nuclei, STN, GPe (external segment of globus pallidus), GPi, and thalamocortical (TC) cell related to PD. Another major contribution of this work is that they defined a criteria of DBS effectiveness; that is, the fidelity of TC relaying sensorimotor signals. In their computational model of parkinsonian conditions, rhythmic inhibition from GPi to the thalamus compromises the TC relay ability to respond faithfully to sensorimotor signals arriving at the thalamus via corticothalamic projections. Under the GPi inhibition altered by the conventional DBS, TC neurons respond faithfully to incoming sensorimotor signals, and then the conventional DBS achieves clinical effectiveness. This criteria later was further validated by incorporating experimental and human data into a model of TC relay neurons by Guo et al. [26, 27]. The scope of Rubin and Terman’s work [66] was to probe the working mechanism of the conventional DBS. It is a logical next step to build upon their network model and further develop better alternatives to the conventional DBS [66].
MDFS Using a Biophysical Model
Guo and Rubin [25] reported the first work of STN stimulation in the form of MDFS with a biophysical–detailed basal ganglia network model based on Rubin and Terman’s model [66]. In [25], both inhibitory population GPe, GPi, and excitatory population STN are included. There is no self–coupling among the excitatory STN neurons. Therefore the synchronized bursting clusters in STN are not induced by strong excitatory self—coupling such as previous work [34, 35, 36, 64, 77]. The synchronized clusters exist because of the topological structure and coupling between different neuronal groups. Such a setup is consistent with the basal ganglia anatomy that there is not synaptic coupling among excitatory STN neurons [32]. Guo and Rubin demonstrated that MDFS applied in STN population not only breaks the pathological synchrony, but also eliminates the bursting patterns presented in STN neurons. The reduction of the average firing rate is a natural result from the burst elimination. They further evaluated the outcome of MDFS by looking at the TC relay fidelity. Their results show that MDFS restores the TC relay ability by desynchronization and burst elimination in a parkinsonian basal–ganglia thalamocortical network. Even though they have some success in this first attempt, the network they consider in their model is too small and the spatial structure of the neurons is too rigid to be representative of the real basal ganglia circuit in [25]. There are only tens of neurons in the basal–ganglia network including GPe, STN, and GPi nuclei (16 in each type). Guo and Rubin placed 16 STN neurons spatially in a perfect symmetric square grid. They measured LFP from the center of the STN neurons and fed the filtered LFP signal back to STN through four symmetric stimulation sites. Little is known about the geometric structure of the STN neurons. However, the assumption of perfect symmetry of these neurons is an unrealistic extreme. Moreover, the symmetry in STN neurons and stimulation sites eliminates many possible variations in the administration of MDFS. One natural question that follows is whether MDFS may still be able to restore TC relay fidelity if the network is larger with non-symmetric stimulation sites among randomly placed neurons.
Other Computational Study on DBS
Dovzhenok and others [18] studied the action of DBS on partially synchronized oscillatory dynamics. Their basal ganglia model, based on the RT model, consisted of two populations: an array of 20 GPe neurons and an array of 10 STN neurons that was tuned to reproduce experimentally recorded data in parkinsonian conditions. They generated the LFP feedback signal by considering only the stimulation current, the synaptic current flowing into the neuron and the synaptic currents flowing into the two closest STN neighbors. They excludes all the ionic currents of STN neurons in the calculation of LFP signal, unlike other computational work including the ionic currents [26, 34, 35, 36, 45, 64, 77]. They concluded that DBS is more likely to increase the synchrony in the basal ganglia thereby increasing PD symptoms. Their findings, opposite to many other computation results [25, 26, 34, 35, 36, 45, 64, 77] and experimental results [44], may be due to the exclusion of ionic currents in the LFP calculation.
Lourens [45] augmented the model by Terman et al. [76], which is the prelude of the RT model, with spike timing dependent plasticity (STDP) for the inhibitory connections within the GPe. He showed that a STDP rule that regulates the synaptic weights between GPe cells stabilizes the two possible coexisting network states, a healthy state (desynchronized) and a PD state (synchronized). Since STDP can learn the good (desynchronized) dynamics or bad (synchronized) dynamics by changing its synaptic connections between GPe neurons, DBS can teach the network with STDP to transition to more healthy activity by forcing the network in a healthy activity region. He showed that constant DBS has a counterproductive effect on PD since the STDP moves the network to a more synchronized state once the DBS is removed. But a short duration DBS with sufficiently high amplitude can use STDP to move the PD network to a healthier state.
Gorzelic and others [20] explored the use of classical feedback control methods in the application of DBS. Gorzelic et al. used the model from [67] consisting of 8 STN neurons, 8 GPe neurons, 8 GPi neurons and 2 TC cells to develop and test model–based rational feedback controller design. They tested two high level control strategies: one of which was driven by online estimate of thalamic reliability (reliability–based control) and another that acts to eliminate substantial decreases in the inhibition from GPi to the thalamus (GPi synaptic conductance control). They designed six control laws that are inspired by the proportional–integral–derivative (PID) methodology. They concluded that best controller based on performance was the amplitude proportional with derivative control and integral bias, which is a full PID controller. Their findings suggested that model–based rational design of feedback controllers for PD can play an important role in the development of closed loop DBS.
Scope of the Current Work
We study a form of closed–loop DBS that has been suggested as an alternative to the conventional DBS, namely multi–site STN stimulation (MDFS) with delays between stimulation periods at different stimulation sites [34, 36, 75]. We consider such stimulation with the current injection based on a local field potential signal recorded from the STN population [25, 34, 35, 64, 77]. To perform our investigation, we introduce this stimulation paradigms into a computational model based on earlier work [25, 26, 67, 76]. This model consists of a neural network of conductance–based STN, GPe, GPi, and TC neurons that, by design, generates parkinsonian activity patterns in the absence of stimulation. Our goal is to explore the impact of closed–loop MDFS on TC relay fidelity. We will further compare TC relay performance with basal ganglia modulation across PD state and PD state with MDFS and other types of DBS, such as the conventional DBS, coordinated reset periodic DBS.
The main goal of the current work is to explore whether the closed–loop MDFS can improve thalamic relay responses in parkinsonian conditions modeled by a network of conductance–based, single–compartment computational neurons. In section “Computational Model of Basal Ganglia Thalamic Network”, as the first step, we will introduce such a network model of parkinsonian conditions and the measure of the TC relay fidelity, both adopted from earlier work [25, 66, 76]. In section “Multi–site Delayed Feedback Stimulation”, we will give details on how to administrate closed–loop MDFS and do a comparison study between open–loop and closed–loop DBS. In the final section, we will review results on TC relay fidelity with experimental and human recording data of GPi neurons to validate our evaluation criteria of DBS, based on TC relay error index.
Computational Model of Basal Ganglia Thalamic Network
To develop a biologically faithful PD network model, we will adopt the same Hodgkin–Huxley model of basal ganglia thalamic network as in [25, 66, 76] with modifications to incorporate MDFS stimulation. Neurons in the basal ganglia and the thalamus communicate through various excitatory and inhibitory synaptic connections and receive certain external inputs. The basal ganglia circuit consists of GPe, GPi, STN neurons, and striatal input as shown on Fig. 4.1. All straight lines with arrows represent synaptic connections or inputs. Both GPi and GPe receive excitatory inputs from STN. GPe and GPi are subject to a constant, inhibitory striatal input. There is synaptic coupling among inhibitory GPe neurons, and there is no coupling within the STN population and the GPi population. The thalamocortical (TC) cell is a relay station whose role is to respond under the GPi inhibition to incoming sensorimotor excitation via corticothalamic projections.
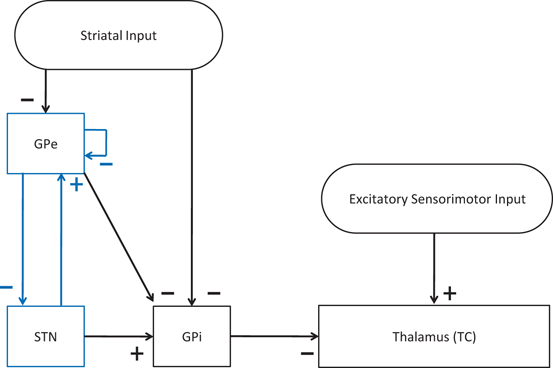

Fig. 4.1
Neuronal structure in the network model. Arrows labeled with a ‘−’ sign represent inhibitory synaptic connections or inputs. Arrows labeled with a ‘+’ sign are excitatory synaptic connections or inputs
Model Equations for STN, GPe and GPi Neurons
The network model consists of TC, STN, GPe, and GPi neurons. We will first describe the equations of STN, GPe and GPi neuron in the model network [25, 66, 76]. Then we give the details of the conductance–based model equations for the TC neuron and the error index to measure TC relay [25, 26, 66], which we use to evaluate the DBS effectiveness in later sections. All specifics of the functions and parameter values used for each type of neuron in the model are given in the Appendix.
STN Neurons
The STN voltage equation that we use, of the form
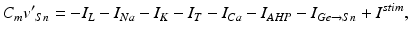
was introduced in [76]. All the currents and corresponding kinetics are the same except that we make some parameter adjustments so that STN firing patterns are more similar to those reported in vivo [7, 78, 79]. 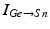 is the inhibitory input current from GPe to STN.
is the inhibitory input current from GPe to STN. 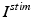 is the external stimulation applied to STN, which is multi–site coordinated reset stimulation (CRS), multi–site stimulation based on the local field potential (LFP), or conventional high frequency stimulation. The details of these types of stimulation will be discussed further in sections “Multi–site Delayed Feedback Stimulation”.
is the external stimulation applied to STN, which is multi–site coordinated reset stimulation (CRS), multi–site stimulation based on the local field potential (LFP), or conventional high frequency stimulation. The details of these types of stimulation will be discussed further in sections “Multi–site Delayed Feedback Stimulation”.
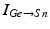 is the inhibitory input current from GPe to STN.
is the inhibitory input current from GPe to STN. 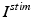 is the external stimulation applied to STN, which is multi–site coordinated reset stimulation (CRS), multi–site stimulation based on the local field potential (LFP), or conventional high frequency stimulation. The details of these types of stimulation will be discussed further in sections “Multi–site Delayed Feedback Stimulation”.
is the external stimulation applied to STN, which is multi–site coordinated reset stimulation (CRS), multi–site stimulation based on the local field potential (LFP), or conventional high frequency stimulation. The details of these types of stimulation will be discussed further in sections “Multi–site Delayed Feedback Stimulation”.GPe Neurons
The voltage of each model GPe neuron obeys the equation
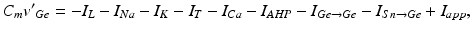
where 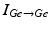 is the inhibitory input from other GPe cells,
is the inhibitory input from other GPe cells, 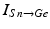 is the excitatory input from STN cells, and
is the excitatory input from STN cells, and 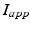 is a constant external current that represents hyperpolarizing striatal input to all GPe cells.
is a constant external current that represents hyperpolarizing striatal input to all GPe cells.
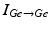 is the inhibitory input from other GPe cells,
is the inhibitory input from other GPe cells, 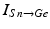 is the excitatory input from STN cells, and
is the excitatory input from STN cells, and 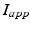 is a constant external current that represents hyperpolarizing striatal input to all GPe cells.
is a constant external current that represents hyperpolarizing striatal input to all GPe cells.GPi Neurons
The voltage equation for each model GPi neuron is similar to that for the GPe neurons, namely
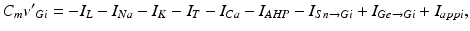
where 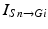 represents the excitatory input from STN to GPi,
represents the excitatory input from STN to GPi, 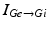 is the inhibitory input from GPe to GPi, and
is the inhibitory input from GPe to GPi, and 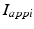 are constant external inputs that represent hyperpolarizing currents from striatum to all GPi cells.
are constant external inputs that represent hyperpolarizing currents from striatum to all GPi cells.
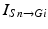 represents the excitatory input from STN to GPi,
represents the excitatory input from STN to GPi, 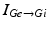 is the inhibitory input from GPe to GPi, and
is the inhibitory input from GPe to GPi, and 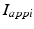 are constant external inputs that represent hyperpolarizing currents from striatum to all GPi cells.
are constant external inputs that represent hyperpolarizing currents from striatum to all GPi cells.TC Neuron and Its Relay Responses
The model for each TC neuron takes the form
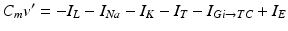
(4.1)
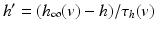
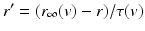
In system (1), 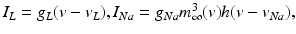 and
and 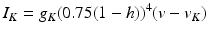 are leak, sodium, and potassium currents, respectively. We apply a standard reduction in our expression for the potassium current to decrease the dimensionality of the model by one variable [62]. The current
are leak, sodium, and potassium currents, respectively. We apply a standard reduction in our expression for the potassium current to decrease the dimensionality of the model by one variable [62]. The current 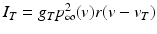 is a low–threshold calcium current, where
is a low–threshold calcium current, where 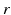 is the inactivation and
is the inactivation and 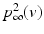 is the activation. The membrane capacitance
is the activation. The membrane capacitance 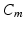 is normalized to 1
is normalized to 1 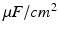 in all the neural models included in the current work.
in all the neural models included in the current work.
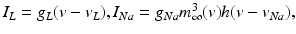 and
and 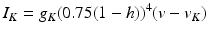 are leak, sodium, and potassium currents, respectively. We apply a standard reduction in our expression for the potassium current to decrease the dimensionality of the model by one variable [62]. The current
are leak, sodium, and potassium currents, respectively. We apply a standard reduction in our expression for the potassium current to decrease the dimensionality of the model by one variable [62]. The current 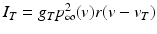 is a low–threshold calcium current, where
is a low–threshold calcium current, where 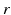 is the inactivation and
is the inactivation and 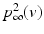 is the activation. The membrane capacitance
is the activation. The membrane capacitance 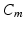 is normalized to 1
is normalized to 1 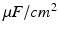 in all the neural models included in the current work.
in all the neural models included in the current work.Additional terms in system (4.1) are inputs that the model TC neuron receives. One is the inhibitory input current from the GPi, 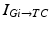 , such that
, such that
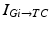 , such that
, such that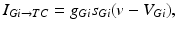
(4.2)
where 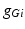 is the constant maximum conductance and
is the constant maximum conductance and 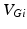 is the synaptic reversal potential.
is the synaptic reversal potential. 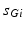 satisfies the equation
satisfies the equation
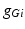 is the constant maximum conductance and
is the constant maximum conductance and 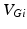 is the synaptic reversal potential.
is the synaptic reversal potential. 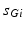 satisfies the equation
satisfies the equation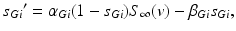
(4.3)
where
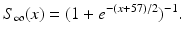
The other input to the model TC neuron, 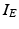 , represents simulated excitatory sensorimotor signals to the TC neuron. We assume that these are sufficiently strong to induce a spike in the absence of inhibition and therefore may represent synchronized inputs from multiple presynaptic cells. We tune the parameters so that the TC cell yields spontaneous spikes at rate of roughly 12 Hz in the absence of both inhibitory GPi and excitatory synaptic inputs. The parameter values chosen place the model TC neuron near transition from silence to spontaneous oscillations. In the model,
, represents simulated excitatory sensorimotor signals to the TC neuron. We assume that these are sufficiently strong to induce a spike in the absence of inhibition and therefore may represent synchronized inputs from multiple presynaptic cells. We tune the parameters so that the TC cell yields spontaneous spikes at rate of roughly 12 Hz in the absence of both inhibitory GPi and excitatory synaptic inputs. The parameter values chosen place the model TC neuron near transition from silence to spontaneous oscillations. In the model, 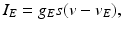 where
where 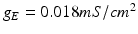 , and
, and  satisfies equation
satisfies equation
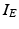 , represents simulated excitatory sensorimotor signals to the TC neuron. We assume that these are sufficiently strong to induce a spike in the absence of inhibition and therefore may represent synchronized inputs from multiple presynaptic cells. We tune the parameters so that the TC cell yields spontaneous spikes at rate of roughly 12 Hz in the absence of both inhibitory GPi and excitatory synaptic inputs. The parameter values chosen place the model TC neuron near transition from silence to spontaneous oscillations. In the model,
, represents simulated excitatory sensorimotor signals to the TC neuron. We assume that these are sufficiently strong to induce a spike in the absence of inhibition and therefore may represent synchronized inputs from multiple presynaptic cells. We tune the parameters so that the TC cell yields spontaneous spikes at rate of roughly 12 Hz in the absence of both inhibitory GPi and excitatory synaptic inputs. The parameter values chosen place the model TC neuron near transition from silence to spontaneous oscillations. In the model, 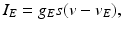 where
where 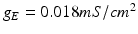 , and
, and 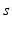 satisfies equation
satisfies equation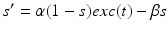
where 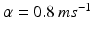 and
and 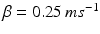 . The function
. The function 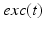 controls the onset and offset of the excitation:
controls the onset and offset of the excitation: 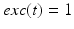 during each excitatory input, whereas
during each excitatory input, whereas 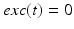 between excitatory inputs. The periodic
between excitatory inputs. The periodic 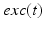 takes the following form:
takes the following form:
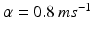 and
and 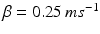 . The function
. The function 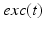 controls the onset and offset of the excitation:
controls the onset and offset of the excitation: 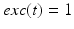 during each excitatory input, whereas
during each excitatory input, whereas 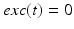 between excitatory inputs. The periodic
between excitatory inputs. The periodic 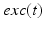 takes the following form:
takes the following form: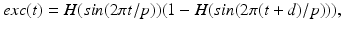
where the period 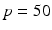 ms and duration
ms and duration 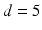 ms, and
ms, and 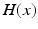 is the Heaviside step function, such that
is the Heaviside step function, such that 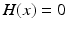 if
if 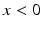 and
and 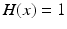 if
if 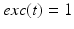 from time
from time 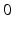 up to time
up to time 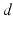 , from time
, from time 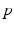 up to time
up to time 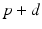 , from time
, from time 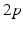 up to time
up to time 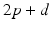 , and so on. A similar periodic function was used in previous work [25, 26, 66]. A baseline input frequency of 20 Hz is consistent with the high–pass filtering of corticothalamic inputs observed in vivo [13]; at this input rate, the model TC cells rarely fire spontaneous spikes between inputs.
, and so on. A similar periodic function was used in previous work [25, 26, 66]. A baseline input frequency of 20 Hz is consistent with the high–pass filtering of corticothalamic inputs observed in vivo [13]; at this input rate, the model TC cells rarely fire spontaneous spikes between inputs.
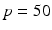 ms and duration
ms and duration 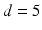 ms, and
ms, and 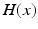 is the Heaviside step function, such that
is the Heaviside step function, such that 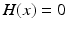 if
if 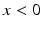 and
and 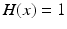 if
if 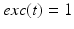 from time
from time 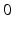 up to time
up to time 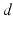 , from time
, from time 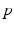 up to time
up to time 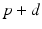 , from time
, from time 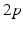 up to time
up to time 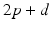 , and so on. A similar periodic function was used in previous work [25, 26, 66]. A baseline input frequency of 20 Hz is consistent with the high–pass filtering of corticothalamic inputs observed in vivo [13]; at this input rate, the model TC cells rarely fire spontaneous spikes between inputs.
, and so on. A similar periodic function was used in previous work [25, 26, 66]. A baseline input frequency of 20 Hz is consistent with the high–pass filtering of corticothalamic inputs observed in vivo [13]; at this input rate, the model TC cells rarely fire spontaneous spikes between inputs.We evaluate the TC relay fidelity in the parkinsonian network and the performance of all stimulation protocols through calculating the TC relay error index defined as
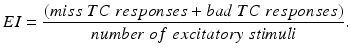
(4.4)
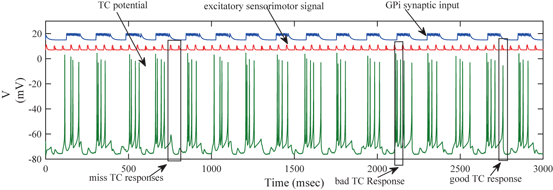
We will use an existing algorithm by Guo et al. [25, 26, 27] to identify good, miss and bad TC responses and count the number of each type of TC responses. A good TC response (see example on Fig. 4.6) refers to one single TC spike corresponding to one sensorimotor input (the small bumps of the middle trace on Fig. 4.6) within a designated time window and before the next input arrives. In a “normal” state, a TC relay cell generates good TC responses to most of excitatory sensorimotor inputs. In a parkinsonian state, the thalamus is no longer able to transmit sensorimotor signals faithfully. Two types of TC relay error occur: one is bad TC relay response, the other is miss TC relay response (see examples in Fig. 4.6). The algorithm to determine a bad or miss response counts at most one error per excitatory sensorimotor input [25, 26, 66]. Therefore, 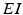 should be a value between 0 and 1.
should be a value between 0 and 1.
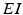 should be a value between 0 and 1.
should be a value between 0 and 1.Model Design of a Parkinsonian Network
We design a model of parkinsonian network which consists STN, GPe, GPi and TC neurons introduced in sections “Model Equations for STN, GPe and GPi Neurons” and “TC Neuron and Its Relay Responses”. Each STN, GPe, and GPi group includes 112 neurons. We incorporated two relay TC neurons into the parkinsonian network to evaluate the performance of DBS. The current parkinsonian network model is significantly advanced from the previous toy network that only has 16 neurons in each group [25, 66]. The network model mimics the pathological neuronal activity observed in the basal ganglia in parkinsonian conditions, such as increased firing rate, bursting patterns, and synchronization in STN and GPi neurons [4, 8, 9, 38, 43, 47, 54, 61, 83, 84]. We consider this rhythmic clustered regime in STN and GPi as the parkinsonian state and refer to the network in this state as the parkinsonian network. In the following subsections, we focus on three aspects of the PD network model: the coupling structure in the STN–GPe loop, the averaged GPi synaptic input going into a TC relay neuron, and the TC relay error index.
Coupling Within the STN–GPe Loop
One important feature of the PD network depicted on Fig. 4.1 is its capability of inducing rhythmic bursting patterns in GPi cells to mimic those seen experimentally in parkinsonian conditions [25, 26]. Since each GPi neuron receives synaptic inputs from a single corresponding STN neuron and a single GPe neuron, the rhythmic, bursting, and synchronized activity in a group of GPi neurons is really induced by the upstream structure of STN-GPe subnetwork that forms a loop. (See GPe and STN neurons with arrows between them and the arrow starting from GPe and back to itself on Fig. 4.1.) Therefore, it is crucial to set up appropriate coupling among the STN–GPe loop.
As shown previously [76], the STN and GPe subnetwork can generate both irregular asynchronous and synchronous activity [5, 59, 76]. In [25], Guo and Rubin designed a small STN–GPe network with specific symmetry and asymmetry in the coupling of sub–populations of STN and GPe, each of which has only 16 neurons. Each STN cells receives a designated inhibition signal from a GPe cell. And the STN cells are segregated into two groups and provide excitation via the design of strong and weak coupling back to GPe cells which are also segregated into two clusters.
Based on previous work [25, 66, 76], we successfully design a parkinsonian network relying on the coupling structure of the STN/GPe loop in a much larger network with many more neurons. We demonstrate that the STN cells in the two segregated groups can form two rhythmically bursting clusters. Figure 4.2 shows the synchronized clusters in the STN population of the PD network model. Half of the 112 STN neurons are in one synchronized bursting cluster, and the other half forms the second synchronized bursting cluster.
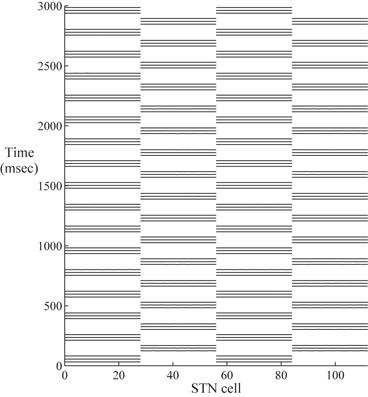

Fig. 4.2
Two synchronized STN clusters. The horizontal axis is the STN cell index. STN cell 1–28 and cell 57–84 form one synchronized cluster. Cell 29֪–56 and 85–112 form the second synchronized cluster. The horizontal bars represent spike times. Since STN cell 1–28 are in perfect synchrony, we only see one long bar across cell 1–28
The detailed structure of connections between STN and GPe neurons is depicted on Fig. 4.3. The synaptic connections within the STN–GPe loop are structured sparsely according to [66]. The STN–GPe loop consists of two subpopulations of 56 STN neurons and 56 GPe neurons each. The neurons in one subpopulation, mainly the STN neurons are connected to the GPe neurons in the other subpopulation via weak synaptic connections (all dashed lines with an arrow on Fig. 4.3). Each subpopulation is further divided into four groups of 14 neurons, (four blocks in each row on Fig. 4.3. Each group of 14 STN are connected to two groups of 14 GPe neurons through strong excitation (all black lines with an arrow on Fig. 4.3). Each group of 14 GPe cells sends strong inhibition to two groups of 14 STN neurons (all black lines with a solid circle on Fig. 4.3). There is also self coupling among GPe neurons. With the connections demonstrated on Fig. 4.3, the four groups of STN neurons (total 56) in the second row of Fig. 4.3, with 14 in each group, form one bursting cluster, and the fourth row of total 56 STN neurons forms the second bursting cluster. Then the STN–GPe loop sends excitation (from the STN neurons) and inhibition (from the GPe neurons) to the downstream GPi neurons, which cause the GPi model neurons to imitate the activity seen experimentally in monkeys with drug induced PD or humans with PD.
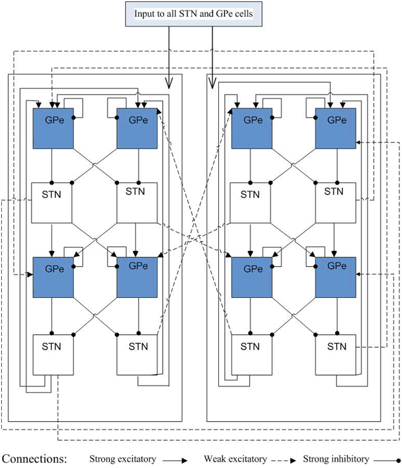

Fig. 4.3
Coupling structure in the STN–GPe loop. Top row of GPe neurons with total 56, 14 in each block, are in one cluster. The second row includes 56 synchronized bursting STN neurons with 14 in each block. Similar structures in the third and fourth row. Solid line with an arrow and solid line with a solid circle represent strong excitatory and inhibitory connections, respectively. Dashed line with an arrow is weak excitatory coupling
Averaged GPi Synaptic Input to a TC Cell
The network model includes 112 GPi neurons in the downstream of the STN–GPe loop. Each GPi cell receives input from a single corresponding STN neuron. Thus, the synchronized, rhythmic, bursting outputs of each STN cluster induce rhythmic, bursting and synchronized activity in a corresponding group of GPi neurons. Figure 4.4 shows the bursting pattern of one GPi neuron in the PD network we designed.
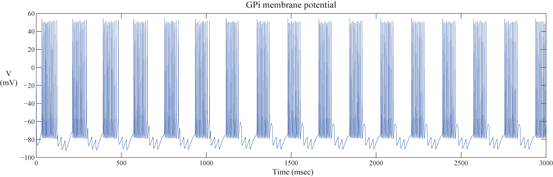

Fig. 4.4
The Membrane potential of a GPi neuron in a parkinsonian network model
To further correlate the population effect of the synchronized GPi bursts to a TC neuron, we compute averaged GPi synaptic input over half of the GPi population who fire synchronized bursts in the PD network. In our network, the synaptic input from GPi to a TC neuron, 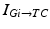 , comes from a subgroup of GPi neurons. This input takes the form
, comes from a subgroup of GPi neurons. This input takes the form
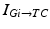 , comes from a subgroup of GPi neurons. This input takes the form
, comes from a subgroup of GPi neurons. This input takes the form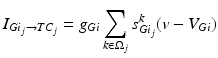
(4.5)
where 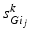 satisfies Eq. (4.3). We define
satisfies Eq. (4.3). We define
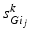 satisfies Eq. (4.3). We define
satisfies Eq. (4.3). We define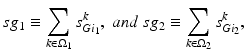
where 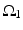 is one synchronized subgroup which consists of 56 GPi cells,
is one synchronized subgroup which consists of 56 GPi cells, 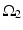 is the other synchronized subgroup with the same number of GPi cells.
is the other synchronized subgroup with the same number of GPi cells. 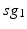 , the total synaptic input from GPi neurons in group
, the total synaptic input from GPi neurons in group 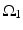 going into TC cell 1, is the top trace shown on Fig. 4.6.
going into TC cell 1, is the top trace shown on Fig. 4.6. 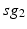 is the total synaptic input from GPi neurons in group
is the total synaptic input from GPi neurons in group 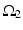 going into TC cell 2 (not shown).
going into TC cell 2 (not shown).
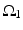 is one synchronized subgroup which consists of 56 GPi cells,
is one synchronized subgroup which consists of 56 GPi cells, 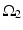 is the other synchronized subgroup with the same number of GPi cells.
is the other synchronized subgroup with the same number of GPi cells. 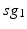 , the total synaptic input from GPi neurons in group
, the total synaptic input from GPi neurons in group 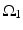 going into TC cell 1, is the top trace shown on Fig. 4.6.
going into TC cell 1, is the top trace shown on Fig. 4.6. 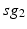 is the total synaptic input from GPi neurons in group
is the total synaptic input from GPi neurons in group 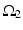 going into TC cell 2 (not shown).
going into TC cell 2 (not shown).Based on the form of Eq. (4.3), each 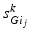 is between 0 and 1, and hence
is between 0 and 1, and hence ![$$s{{g}_{i}}\in [0,56]$$](/wp-content/uploads/2016/12/A319630_1_En_4_Chapter_IEq55.gif) ,
, 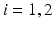 for each
for each 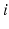 . In our simulations, we use the variability of the time–average of each
. In our simulations, we use the variability of the time–average of each 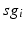 as an indicator of GPi rhythmicity. Specifically, we form histograms based on the frequency with which each
as an indicator of GPi rhythmicity. Specifically, we form histograms based on the frequency with which each 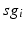 time course, averaged over 5 ms time windows, takes different values in bins that cover the range
time course, averaged over 5 ms time windows, takes different values in bins that cover the range ![$$[0,56]$$](/wp-content/uploads/2016/12/A319630_1_En_4_Chapter_IEq60.gif) . We display five bins centered at 5 through 45 with increment 10. In the parkinsonian network without stimulation, the average
. We display five bins centered at 5 through 45 with increment 10. In the parkinsonian network without stimulation, the average 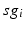 values mostly fall into the first bin centered at 5 and the fifth bin centered at 45, as displayed on Fig. 4.5. This result occurs because GPi firing is rhythmic and bursting (see the top traces on Fig. 4.6), such that GPi synaptic output is high during each burst and low between bursts. A few values do fall into the middle bins, due to transition between bursting and quiescent phases. However, very different results emerge when stimulation is applied to the STN neurons (Fig. 4.10 in section “Results” and Fig. 4.14 in section “Comparison Between Open–Loop and Closed–Loop Stimulations”).
values mostly fall into the first bin centered at 5 and the fifth bin centered at 45, as displayed on Fig. 4.5. This result occurs because GPi firing is rhythmic and bursting (see the top traces on Fig. 4.6), such that GPi synaptic output is high during each burst and low between bursts. A few values do fall into the middle bins, due to transition between bursting and quiescent phases. However, very different results emerge when stimulation is applied to the STN neurons (Fig. 4.10 in section “Results” and Fig. 4.14 in section “Comparison Between Open–Loop and Closed–Loop Stimulations”).
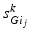 is between 0 and 1, and hence
is between 0 and 1, and hence ![$$s{{g}_{i}}\in [0,56]$$](/wp-content/uploads/2016/12/A319630_1_En_4_Chapter_IEq55.gif) ,
, 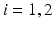 for each
for each 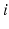 . In our simulations, we use the variability of the time–average of each
. In our simulations, we use the variability of the time–average of each 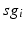 as an indicator of GPi rhythmicity. Specifically, we form histograms based on the frequency with which each
as an indicator of GPi rhythmicity. Specifically, we form histograms based on the frequency with which each 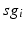 time course, averaged over 5 ms time windows, takes different values in bins that cover the range
time course, averaged over 5 ms time windows, takes different values in bins that cover the range ![$$[0,56]$$](/wp-content/uploads/2016/12/A319630_1_En_4_Chapter_IEq60.gif) . We display five bins centered at 5 through 45 with increment 10. In the parkinsonian network without stimulation, the average
. We display five bins centered at 5 through 45 with increment 10. In the parkinsonian network without stimulation, the average 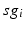 values mostly fall into the first bin centered at 5 and the fifth bin centered at 45, as displayed on Fig. 4.5. This result occurs because GPi firing is rhythmic and bursting (see the top traces on Fig. 4.6), such that GPi synaptic output is high during each burst and low between bursts. A few values do fall into the middle bins, due to transition between bursting and quiescent phases. However, very different results emerge when stimulation is applied to the STN neurons (Fig. 4.10 in section “Results” and Fig. 4.14 in section “Comparison Between Open–Loop and Closed–Loop Stimulations”).
values mostly fall into the first bin centered at 5 and the fifth bin centered at 45, as displayed on Fig. 4.5. This result occurs because GPi firing is rhythmic and bursting (see the top traces on Fig. 4.6), such that GPi synaptic output is high during each burst and low between bursts. A few values do fall into the middle bins, due to transition between bursting and quiescent phases. However, very different results emerge when stimulation is applied to the STN neurons (Fig. 4.10 in section “Results” and Fig. 4.14 in section “Comparison Between Open–Loop and Closed–Loop Stimulations”).
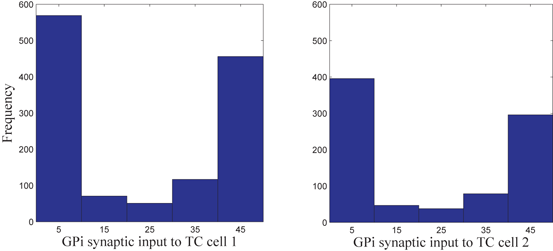
Fig. 4.5
Histograms of time-averaged 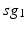 (left) and
(left) and 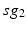 (right) in the parkinsonian network. Both histograms include two dominant bins, centered at 5 and 45, due to the quiescent and bursting phases, respectively, of GPi activity
(right) in the parkinsonian network. Both histograms include two dominant bins, centered at 5 and 45, due to the quiescent and bursting phases, respectively, of GPi activity
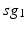 (left) and
(left) and 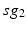 (right) in the parkinsonian network. Both histograms include two dominant bins, centered at 5 and 45, due to the quiescent and bursting phases, respectively, of GPi activity
(right) in the parkinsonian network. Both histograms include two dominant bins, centered at 5 and 45, due to the quiescent and bursting phases, respectively, of GPi activity
Fig. 4.6
The membrane potentials of a TC neuron responding to excitatory sensorimotor signals (middle trace), along with the total synaptic input the neuron receives from 56 GPi neurons (top trace). Note that the vertical axis label applies to the voltage trace, while the latter two traces are placed and scaled arbitrarily. Also, observe that the total GPi synaptic input is rhythmic and bursting, representing parkinsonian conditions
TC Relay in the PD Network
In the parkinsonian network we designed, the synaptic input from GPi to TC (the top trace on Fig. 4.6) appears to be rhythmic and bursting. Although the TC neuron responds with a single spike (a good TC response shown on Fig. 4.6) to some of the excitatory inputs that it receives, others elicit either no spikes, or multiple spikes, which are miss TC responses and bad TC responses, respectively (both are shown on Fig. 4.6). Overall, the TC relay error is apparently at the higher end towards 1 in the parkinsonian network.
Multi–site Delayed Feedback Stimulation
We focus on investigating MDFS in a large biophysical network model of basal ganglia and thalamus. The objective is to gain understanding on how the MDFS form of closed–loop DBS might achieve its therapeutic effectiveness by the proper selection of stimulation target sites and parameters. In particular, using a scaled up basal ganglia thalamocortical parkinsonian network with hundreds of neurons, we develop a closed–loop feedback stimulation protocol applied on STN that can restore TC relay ability. The MDFS closed–loop stimulation is based on the LFP signal of the STN population, then is applied to the same STN neurons through multiple stimulation sites. See the schematic demonstration of MDFS being applied to the STN population on Fig. 4.7. In the following sections, we describe the choice of the stimulation sites, the generation of the stimulation currents and the improvement of TC relay during the closed–loop stimulation.
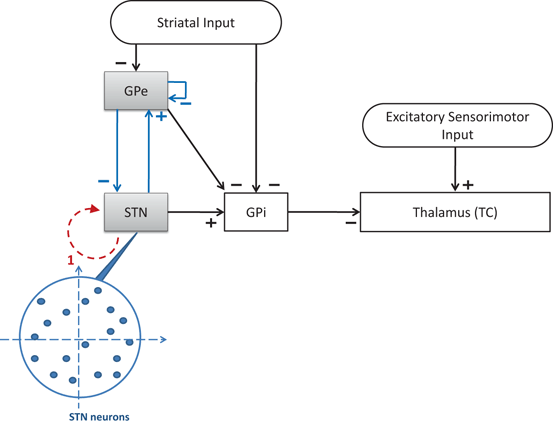

Fig. 4.7
Neuronal structure in the network model. Arrows labeled with a ‘−’ sign represent inhibitory synaptic connections or inputs. Arrows labeled with a ‘+’ sign are excitatory synaptic connections or inputs. The dash arc with an arrow represents the stimulation current. The tail of the dashed arc is where the stimulation current is gathered. The head of the dashed arrow points to the stimulation target population. The blowup shows the random topological structures of stimulation targets–STN with blue arrows representing the STN–GPe loop
Layout Structure and Stimulation Sites of the Target Population
We use two geometric structures for the stimulation target population in the current study. In prior work [25], Guo and Rubin placed 16 STN neurons on a simple four by four square grid where the LFP was collected at the center, and four stimulation sites were chosen symmetrically around the center. This square grid structure is far from the real topology of STN neurons. To improve in this aspect, we use a layout structure of target population on a circle neuronal sheet where all STN neurons are placed both symmetrically (left figure of Fig. 4.8) and randomly (right figure of Fig. 4.8). In the random layout, the positions of neurons are sampled by imposing a minimum distance between any pair of neurons (e.g. excluding two neurons to appear at the same location.) The center of the circle where LFP of the target population is measured and calculated is at the origin of the 2–D plane.
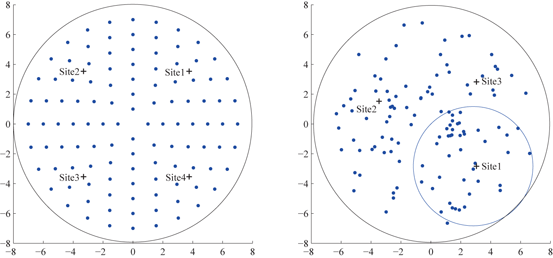

Fig. 4.8
Left symmetric layout of 112 STN neurons on a circle sheet. Four stimulation sites are marked with ‘+’ signs. Right random layout of 112 STN neurons on a circle sheet. Three stimulation sites (marked with ‘+’) are chosen using reference circles. One reference circle centered at site 1, with radius as a half of the neuron circle sheet is shown. LFP is computed by (6) at the center of the neuron sheet in both layouts
Choosing appropriate multiple stimulation sites is a crucial first step to the application of MDFS. Previous study of STN MDFS [25] and work by Hahn and McIntyre [29] have found that the stimulation becomes more effective when it reaches a larger portion of the STN population. In theory, more stimulation sites lead to better outcome of MDFS; however, it is not desirable to have too many stimulation sites as it needs more electrode contact points. In the symmetric layout structure of STN, we choose four stimulation sites symmetrically in the four quarters of the circle (shown on the left figure on Fig. 4.8). In the random layout of STN neurons, to choose proper number and locations of stimulation sites, we define a reference circle with radius as half of the neuronal sheet circle. The reference circle is inside tangent to the circle of neuronal sheet and passes through the center of the neuronal sheet circle. Then we slide the reference circle through the neuronal sheet to identify the most populated region. We place the first stimulation site at the center of the reference circle that contains the most populated region of STN neurons. Then we use a second reference circle to slide through the region not covered by the first reference circle to identify the next most populated region. Overall, we may use up to four reference circles to identify at most four sites to cover at least 85 % of the circle neuronal sheet.
Generation of Stimulation Current from Feedback
We use LFP signal measured and calculated from the center of the circle STN neuronal sheet as the base for the stimulation current. According to current–source density analysis [37, 42, 51, 55], the field potential depends on the linear sum of potentials from sources (currents injected into the extracellular medium) and sinks (current removed from the extracellular medium). For a single point source in a homogeneous medium, the extracellular field potential 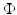 is given by
is given by 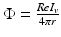 [55], where
[55], where 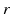 is the distance from the point source,
is the distance from the point source, 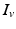 is the current from that point source, and
is the current from that point source, and 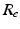 is the constant extracellular resistance. This translates to the following formula for the computation of LFP:
is the constant extracellular resistance. This translates to the following formula for the computation of LFP:
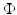 is given by
is given by 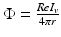 [55], where
[55], where 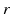 is the distance from the point source,
is the distance from the point source, 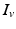 is the current from that point source, and
is the current from that point source, and 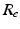 is the constant extracellular resistance. This translates to the following formula for the computation of LFP:
is the constant extracellular resistance. This translates to the following formula for the computation of LFP:Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree





