Chapter 7 Electrical Signaling by Neurons

Inputs to Neurons Cause Slow, Local Potential Changes

Membrane Capacitance and Resistance Determine the Speed and Extent of the Response to a Current Pulse

Membranes Have a Time Constant, Allowing Temporal Summation

Larger-Diameter Neuronal Processes Have Longer Length Constants

All they need to know is, it starts at the bottom and goes to the top, and little things come in, and there you go.

We depend on our brains to process and convey huge quantities of information rapidly and reliably. As a biological system, the brain must do this using neurons and their axons and synapses rather than wires and transistors. This makes the task more difficult, because it is substantially harder to move electrical signals around in the aqueous medium inside and surrounding neurons than in more conventional electronic devices.* The solution used by neurons allows current to be carried not by electrons but rather by the movement of ions, driven by the energy stored in ionic concentration gradients and controlled by molecular switches.

Neurons, as described in Chapter 1, have a complement of organelles comparable to that of other cells, but arrayed in a fashion supporting their signaling functions and their unusual shapes. Like other cells, neurons are also bounded by a semipermeable membrane that is electrically polarized, in this case to a resting membrane potential of about −65 mv. (By convention, the extracellular fluid is considered to be at 0 mv, so a resting potential of −65 mv means that the inside of the cell is 65 mv negative to the outside.) Neurons, however, are masters of moment-to-moment modulation of this membrane potential and use the changes as a signaling mechanism. They use a combination of (1) graded, local potential changes that typically develop and decay relatively slowly and can be compared and summed (e.g., synaptic potentials, receptor potentials) and (2) brief, actively propagated potentials (action potentials) for conveying information over long distances (Fig. 7-1). This chapter describes the biophysical bases for the resting potential, the spread of slow potentials, and the generation and propagation of action potentials. Synaptic potentials are discussed in Chapter 8, and the potentials produced by sensory receptors are addressed in Chapter 9.

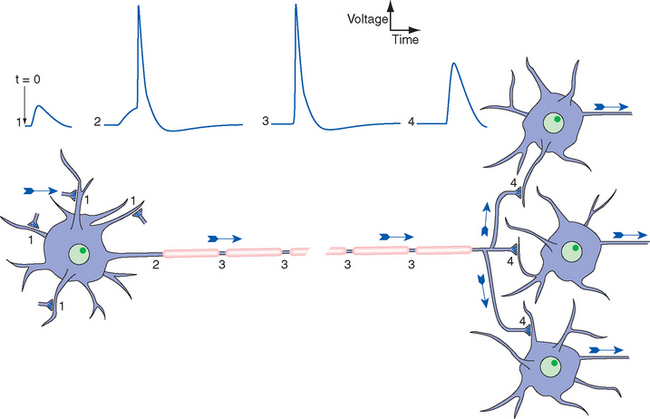
Figure 7-1 General scheme of distribution of electrical signals in the nervous system, with the direction of information flow indicated by arrows. Release of neurotransmitter by synaptic terminals causes slow postsynaptic potentials, as discussed further in Chapter 8. Some are positive-going, or excitatory (1); some are negative-going, or inhibitory (not indicated). Synaptic potentials spread passively to a trigger zone where, if threshold is reached, action potentials are initiated (2). The synaptic potentials die out near the neuronal cell body, but action potentials are propagated actively and without decrement along the axon (3). Action potentials then spread passively into axon terminals (4) and cause the release of neurotransmitter onto other neurons.

A Lipid-Protein Membrane Separates Intracellular and Extracellular Fluids

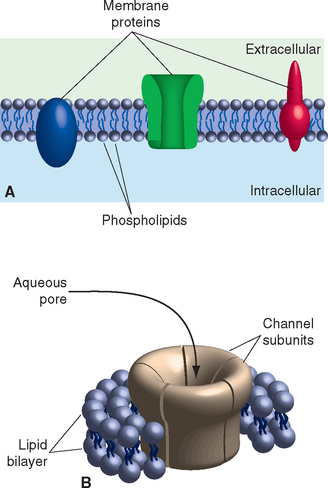
The electrical signaling capabilities of neurons are based on ionic concentration gradients between the intracellular and extracellular compartments (Table 7-1). The cell membrane, a complex of a bilayer of lipid molecules with an assortment of protein molecules embedded in it (Fig. 7-2), separates these two compartments. Concentration gradients are maintained by a combination of selective permeability characteristics and active pumping mechanisms.

Table 7-1 Extracellular and Intracellular Ionic Concentrations of Typical Mammalian Neurons

Figure 7-2 A, Schematic view of part of a neuronal cell membrane, with membrane proteins embedded in a phospholipid bilayer. B, An ion channel consisting of multiple subunits, embedded in the lipid bilayer.

The Lipid Component of the Membrane Is a Diffusion Barrier

The lipid component of the membrane is a double sheet of phospholipids, elongated molecules with polar groups at one end and fatty acid chains at the other (Fig. 7-2). This structure leads to differential activities of the two parts of the molecule when exposed to water (itself a polar molecule): the polar groups are hydrophilic, interacting with water, and the fatty acid tails are hydrophobic, interacting with each other. The consequence is a lipid arrangement in which the fatty acid tails face each other in the center of the membrane and the polar groups face the aqueous solutions inside and outside the neuron. Development of the lipid bilayer was a pivotal event in the evolution of life, because the hydrophobic core prevents diffusion of water-soluble substances and allows the maintenance of concentration gradients across the membrane. The ions that carry the currents used for neuronal signaling are among these water-soluble substances, so the lipid bilayer is also an insulator, the barrier across which membrane potentials develop (see Fig. 7A-3 in Appendix 7A). In biophysical terms, the lipid bilayer is not permeable to ions. In electrical terms, it functions as a capacitor, able to store charges of opposite sign that are attracted to each other but unable to cross the membrane (see Appendix 7A).

Membrane Proteins Regulate the Movement of Solutes across the Membrane

Embedded in the lipid bilayer is a large assortment of proteins, some exposed mainly on the outer or inner surface, but most completely spanning the membrane (Fig. 7-2). Different categories of these proteins have distinctive functions. Some serve as anchor points for cytoskeletal elements; some are surface recognition molecules, participating in physical interactions be-tween neurons and their neighbors or other elements of their extracellular surroundings; some facilitate the movement of lipid-insoluble nutrients such as glucose into neurons. Most important for the purposes of this chapter are proteins that regulate the passage of ions into or out of the cell. Because a lipid bilayer by itself does not allow ions to cross, it cannot be the entire basis for electrical signaling. Certain membrane-spanning proteins confer this ability, either by allowing selected ions to flow down electrical or concentration gradients or by pumping them across.

Ions Diffuse across the Membrane through Ion Channels—Protein Molecules with Pores

Some membrane-spanning proteins consist of several subunits surrounding a central aqueous pore (Fig. 7-2B). Ions whose size and charge “fit” the pore can diffuse through it, allowing these proteins to serve as ion channels. Hence unlike the lipid bilayer, ion channels have an appreciable permeability (or conductance*) to at least some ions. In electrical terms, they function as resistors,† allowing a predictable amount of current flow in response to a voltage across them (see Appendix 7A). Although hundreds of different ion channels have been described, they have some characteristics in common:

1. Multiple states. Most or all ion channels can exist in two or more different, stable conformations. The different conformations fall into two general categories: open, in which the pore is available for ions to traverse, and closed, in which the pore is occluded enough to prevent ion flow. Open channels have high conductance, and closed channels have low conductance, so ion channels are variable resistors; this is the key to their role in membrane potential changes. Remarkably, the transitions between these different conductance states can be observed directly using patch-clamp techniques (Box 7-1; see Fig. 7-17). Most channels in resting neuronal membranes are closed and respond to particular stimuli by opening, although the opposite is also found.

2. Gating. The opening and closing of an individual ion channel is a probabilistic event, and the channel can flip between these states nearly instantaneously. Most channels are tuned to certain factors that affect their probability of being open or closed.‡ Some channels open in response to changes in membrane potential and are referred to as voltage-gated channels (Fig. 7-4A and B). The best understood of these is the voltage-gated sodium channel that underlies action potentials (see Fig. 7-10), but there are also voltage-gated potassium, calcium, and chloride channels. Other channels open or close in response to the binding of signaling molecules (Fig. 7-4C and D). The bound molecule is called a ligand (from the Latin ligare, “to bind”), so these are ligand-gated channels. The best known of these are postsynaptic receptors that bind specific neurotransmitters and change their permeability in response (see Chapter 8), but other channels bind intracellular ligands released in response to various stimuli. Some channels are thermally gated, allowing the neurons that contain them to function as miniature thermometers or as thermal injury detectors (see Chapters 9 and 23). Finally, some channels are mechanically gated. A prominent example is the receptor cells of the inner ear (see Fig. 14-7), but others are known (e.g., see Fig. 23-7).

3. Selectivity. The central pores of ion channels are not wide enough to let any and all ions traverse them. Rather, the size of the pore and the nature of the amino acid residues lining it are such that some ions can diffuse through more easily than others. Some channels are minimally selective and may simply distinguish between small anions and small cations. Others are highly selective and may be, for example, hundreds of times more permeable to sodium ions than to potassium ions.

BOX 7-1 Methods of Measuring Voltages and Currents across Neuronal Membranes

Knowledge of the mechanism of electrical signaling by neurons grew during the 20th century and continues to expand with the development of more sophisticated techniques. Very early work depended on indirect methods, such as measuring currents and voltages in extracellular spaces outside neurons. In the 1930s Hodgkin, Huxley, Katz, Cole, and others began to take advantage of the huge axons that certain invertebrates have developed as a means of increasing conduction velocity (see Fig. 7-22). Methods were devised to thread wires longitudinally through these axons and record currents and voltages directly across the axon membrane.

At about the same time, other workers found that controlled heating and stretching of capillary tubing until it snaps can produce micropipettes with tip diameters smaller than 1 μm. Filled with a salt solution, these micropipettes can be used as electrodes for recording voltages and currents across neuronal membranes; the tip diameter is small enough to puncture many kinds of relatively large neurons without damaging them too much (Fig. 7-3A).

Micropipette electrodes were a mainstay of neurophysiologists for decades, but they always had shortcomings. They damaged small cells and processes, and even when the method was successful, it was possible to record events only across relatively large expanses of membranes. A technique that opened up new horizons appeared in the late 1970s, when Neher and Sakmann developed patch clamping (Fig. 7-3B). Patch clamping makes it possible to record events across the membranes of small cells and processes; even more remarkably, it allows the recording of the activity of individual ion channels in patches of membrane (see Fig. 7-17).

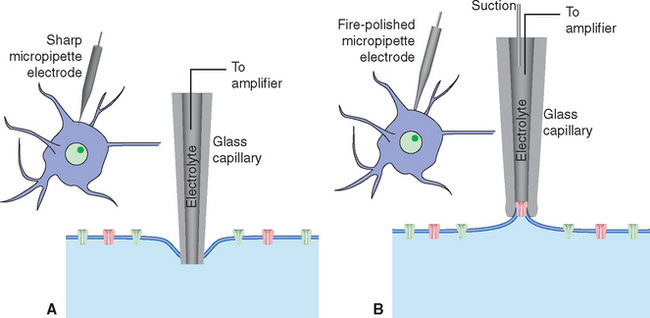
Figure 7-3 Recording electrical activity across neuronal membranes using sharp microelectrodes (A) and patch-clamp electrodes (B). If the tip of a sharp micropipette electrode is small enough, it can be used to impale relatively large neurons with minimal injury. The punctured cell membrane seals around the electrode, and resting transmembrane potentials and potential changes such as those shown in Figure 7-1 can be recorded. Patch-clamp electrodes are generally larger and are prepared with smooth, fire-polished tips. Contact with the surface of a neuron, combined with gentle suction, causes the neuronal membrane to seal onto the pipette tip. Once the seal is established, a series of additional maneuvers allows various recording arrangements: current passing through the attached area of membrane can be measured (see Fig. 7-17); the attached area of membrane can be perforated, creating electrical continuity between the pipette and the cell’s interior and allowing measurement of voltage changes across the cell membrane (referred to as whole-cell recordings; see Fig. 7-13); or the attached membrane patch can be torn away from the cell and exposed to controlled solutions of various sorts while measuring current flows.

Figure 7-17 Abnormal voltage-gated Na⁺ channels in a patient with periodic paralysis. Repeated patch-clamp recordings of the current flowing through single channels of normal muscle membranes (A) and those of the patient (B) during depolarization from 120 to 40 mv indicate that the patient’s channels do not inactivate rapidly. Averages of many such records were used to calculate the probability of channels being open (P_OPEN) over time. The continued, albeit reduced, probability of the patient’s channels being open corresponds to a small but constant inward Na⁺ current that depolarizes the fiber.

(From Cannon SC: Trends Neurosci 19:3, 1996.)

Figure 7-4 Gating properties of ion channels. Voltage-gated channels respond to appropriate voltage changes (in this example, to decreased negativity inside the cell, as in the case of voltage-gated sodium channels) by switching from a closed (A) to an open (B) state. Ligand-gated channels bind specific ligands when available and, in this example, switch from a closed (C) to an open (D) state.

Figure 7-10 The Na⁺ channel cycle. At the normal resting membrane potential, most voltage-gated Na⁺ channels are closed. Depolarization increases the probability of opening. Once open, the channels enter a closed, inactivated state until the membrane is repolarized.

The many different types of ion channels generally are not distributed uniformly in neuronal membranes. Rather, neurons somehow manage to place them preferentially in sites that make functional sense. For example, although the channels that determine the resting membrane potential are widely distributed, voltage-gated sodium channels are grouped so that only certain regions of a neuron can generate action potentials. Similarly, appropriate ligand-gated channels are located in postsynaptic membranes across from presynaptic terminals and not in other locations. This selective regional distribution of channels and other membrane proteins forms much of the basis for the functional specialization of different parts of each neuron.

Small differences in amino acid sequences are sufficient to change the selectivity of a channel, and many channel types are closely related to each other. All the voltage-gated cation channels are the products of one closely related family of genes; some ligand-gated postsynaptic receptors are related to the voltage-gated channels, and others evolved independently. Although the chemical differences between channel types are often subtle, they are nevertheless sufficient to allow pharmacological manipulation of particular channels. This is commonly exploited in the treatment of disease states. Conversely, some diseases are themselves the result of abnormal functioning of particular channel types (see Box 7-2).

BOX 7-2 Channelopathies: Diseases Caused by Defective Ion Channels

Two hereditary muscle diseases with contrasting symptoms provide instructive examples of channelopathies. Patients with periodic paralysis, as the name of the syndrome suggests, have episodes of weakness. Patients with myotonia (“muscle tone”) have difficulty getting muscles to relax once they have contracted.

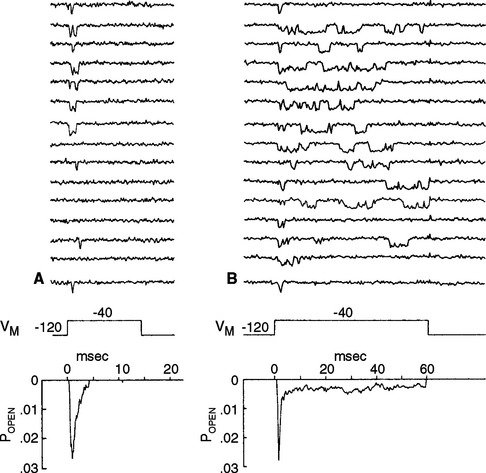
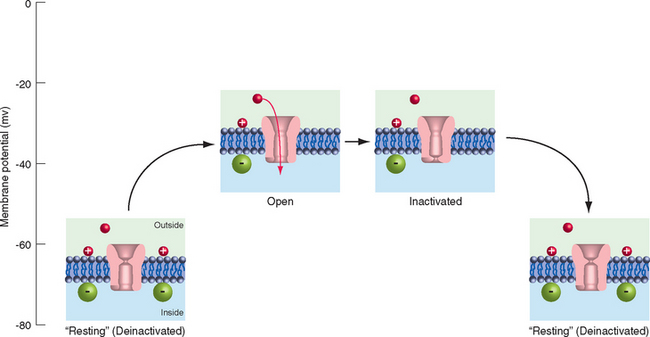
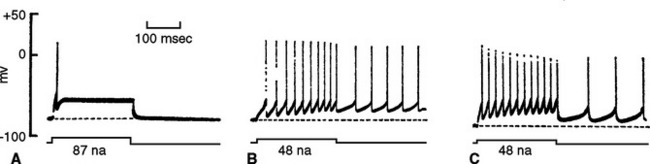
Individuals with hyperkalemic periodic paralysis (one of several types of periodic paralysis) have episodes of weakness and decreased muscle tone that may follow exercise or the consumption of potassium-rich foods, such as fruit juice or bananas. During the attacks, the involved muscle fibers are depolarized by 30 to 40 mv and are unable to fire action potentials. The disorder is caused by a mutation of muscle voltage-gated Na⁺ channels that prevents some percentage of them from inactivating completely after depolarization (Fig. 7-17). This results in a small but constant inward Na⁺ current that depolarizes the fibers, inactivates normal channels, and renders the muscle inexcitable for a period of minutes to hours.

Thomsen’s disease and Becker’s disease are two similar forms of myotonia, inherited in an autosomal dominant and recessive fashion, respectively. The muscles of affected individuals relax unusually slowly following a sudden contraction. It may take several seconds, for example, to unclench a fist, to open a hand after a handshake, or to open the eyes after squinting during a sneeze or during exposure to bright sunlight. Abrupt attempts to run or jump may cause leg muscles to stiffen, resulting in a fall. The mechanism of this form of myotonia was first unraveled by studying the muscle fibers of a strain of goats afflicted by basically the same disease. Myotonic goats, known since the 1880s as “nervous” or “fainting” goats, stiffen up and may fall over when startled.* Normal skeletal muscle fibers, unlike neurons, have a relatively high Cl⁻ permeability, so their resting membrane potential is determined largely by the Cl⁻ concentration gradient. This form of myotonia, in goats as in humans, is caused by a mutation of the Cl⁻ channels that account for most of this resting membrane conductance. The resulting increase in resistance not only makes the membrane time constant longer, so that muscle fibers take longer to repolarize after an action potential, but also reduces the amount of depolarizing current required to reach threshold (Fig. 7-18A and B). In addition, the muscle membrane potential now becomes dominated by the K⁺ concentration, so that small increases in the extracellular K⁺ concentration cause more depolarization than normal. The net result is that a depolarizing stimulus that would cause a single action potential in a normal muscle fiber causes a train of action potentials in a myotonic fiber, in turn causing contraction that is maintained for several seconds. One indication that reduced Cl⁻ conductance is responsible for these properties is the observation that replacing the Cl⁻ in the fluid bathing a normal fiber with an impermeant anion has the same effect (Fig. 7-18C).

^* “If these goats are suddenly surprised or frightened they become perfectly rigid. While in this condition they can be pushed or turned over as if they were carved out of a single piece of wood. This spell or ‘fit’ usually lasts only a short time—about ten to twenty seconds. if two or three men, who had crept up close without being observed, would suddenly rush toward the flock yelling and waving coats in the air a considerable number of the goats would be sure to fall to the ground and most of the rest would become rigid in the upright position for several seconds.” (From Lush JL: J Hered 21:243, 1930.)

Figure 7-18 Effects of decreased Cl⁻ conductance on goat muscle fibers. A, Injection (through a microelectrode) of 87 nanoamperes of current into an intercostal muscle fiber from a normal goat elicits a single action potential. At the termination of the current pulse the membrane potential decays quickly to the original resting potential. B, Injection of little more than half as much current into a muscle fiber from a myotonic goat elicits a train of action potentials. At the termination of the current pulse the membrane stays somewhat depolarized (due to extracellular K⁺ accumulation), and action potentials continue at a slower rate. C, Replacing the Cl⁻ in the solution bathing a normal goat muscle fiber with an impermeant cation (sulfate) causes it to behave like a myotonic fiber.

(From Adrian RH, Bryant SH: J Physiol 240:505, 1974.)

The Number and Selectivity of Ion Channels Determine the Membrane Potential

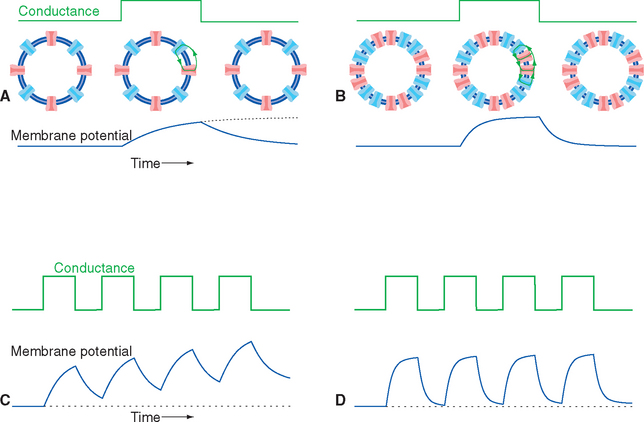
The importance of ion channels in the development of the resting membrane potential is indicated in Figure 7-5. A lipid bilayer separating intracellular and extracellular fluids with the ionic concentrations shown in Table 7-1 would not develop a membrane potential. Even though all the ion species involved (including Ca²⁺, which is not indicated in Fig. 7-5, to keep things a little simpler) are unequally distributed, the impermeability of the membrane would prevent them from moving down their concentration gradients (Fig. 7-5A). The number of positive charges and negative charges on each side of the membrane would be identical.

Figure 7-5 Development and maintenance of a resting membrane potential. A, A lipid bilayer by itself is impermeable, allowing no charge separation to develop. B, Adding K⁺ channels initially results in net movement of K⁺ ions out of the cell (K⁺ ions are free to move in either direction, but because there are more inside the cell, more move from inside to outside than in the opposite direction). C, At equilibrium, a vanishingly small number of excess extracellular K⁺ ions results in cations (mostly Na⁺ ions) lining up on the outside of the membrane, counterbalanced by anions on the inner surface of the membrane. This accounts for the resting membrane potential, which develops abruptly across the membrane. K⁺ ions still flow through their channels, but now equal numbers move out (down the concentration gradient) and in (down the voltage gradient). D, Addition of a small number of Na⁺ channels causes a small inward movement of Na⁺ ions, driven not just by the Na⁺ concentration gradient but also by the intracellular negativity. E, A steady state is reached in which equal numbers of cations move inward and outward across the membrane. However, there is a net inward movement of Na⁺ and outward movement of K⁺. F, The Na⁺/K⁺ ATPase is an exchange pump that compensates for the net Na⁺ and K⁺ fluxes in E.

Consider what would happen if ion channels selectively permeable only to K⁺ were added to such a membrane (Fig. 7-5B). K⁺ ions would be equally free to diffuse into or out of the cell through these channels. However, simply because there are so many more K⁺ ions inside the cell than outside, more K⁺ ions would move out than in (i.e., K⁺ ions would flow out of the cell down the K⁺ concentration gradient). This would leave behind a number of intracellular negative charges. Because opposite charges attract each other, the excess intracellular negative charges would attract K⁺ ions back into the cell. At a time determined by the number of channels available for K⁺ ion movement, the concentration gradient driving K⁺ out of the cell would be exactly counterbalanced by the intracellular negativity; the K⁺ current moving out of the cell would be equal and opposite to the K⁺ current moving into the cell (Fig. 7-5C). The system at this point is in equilibrium: no energy is required to maintain it in this state. The membrane potential at which this equilibrium is reached is the potassium equilibrium potential (V_k); its value can be calculated using a logarithmic relationship called the Nernst equation, knowing only the intracellular and extracellular K⁺ concentrations, the temperature, and some physical constants (see Appendix 7B). Each ion species that is unequally distributed across the membrane has an equilibrium potential that can be calculated in the same way (Table 7-1), indicating the membrane potential that would develop if the membrane were permeable solely to this type of ion (and the potential at which there would be no net movement of that ion in either direction).

The initial net outward movement of K⁺ ions required to establish this membrane potential is actually extremely small—just enough to charge up the membrane capacitance—and no significant change in intracellular or extracellular K⁺ concentration results. For example, the net outward movement of only about 175 million K⁺ ions is enough to establish the predicted membrane potential of −94 mv across the membrane of a spherical cell 100 μm in diameter. Although this sounds like a lot of ions, a cell this size with an intracellular K⁺ concentration of 130 mM contains about 4 × 10¹³ K⁺ ions, so the net loss of K⁺ ions required to establish this membrane potential is less than 0.001% of the starting number! This is a common theme in electrical signaling by neurons: substantial electrical signals can be generated by moving relatively minuscule numbers of ions, so that intracellular and extracellular ionic concentrations change little over brief periods of time. (As will be seen a little later in this chapter, however, active pumping mechanisms are required to maintain ionic concentration gradients over long periods.)

The Resting Membrane Potential of Typical Neurons Is Heavily Influenced, but Not Completely Determined, by the Potassium Concentration Gradient

The scenario just developed is actually close to the situation in typical neurons, whose membrane at rest is dominated by a steady potassium conductance. Hence the resting membrane potential of typical neurons is near the potassium equilibrium potential. Increases in extracellular potassium concentration cause the membrane potential to become less negative, by almost the amount predicted by the Nernst equation (Fig. 7-6). However, the membrane is never quite as negative as the potassium equilibrium potential, and the deviation becomes greater the lower the extracellular potassium concentration becomes.

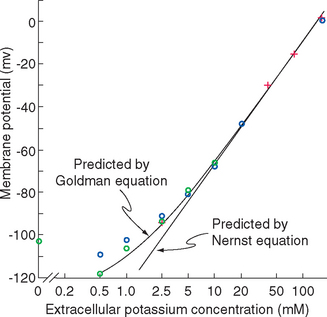
Figure 7-6 The membrane potential of frog muscle fibers at different K⁺ concentrations in the bathing solution. (The membranes of skeletal muscle fibers have properties similar to those of neurons.) Crosses indicate measurements made after the muscle fiber had equilibrated with a new K⁺ concentration for 10 to 60 minutes, blue circles 20 to 60 seconds after an abrupt increase in K⁺ concentration, and green circles 20 to 60 seconds after an abrupt decrease. The curves fitted to the data are provided by equations described in Appendix 7-B.

(Redrawn from Hodgkin AL, Horowicz P: J Physiol 148:127, 1959.)

The basis for this deviation from the membrane potential predicted by the Nernst equation is the additional presence of a relatively small resting permeability to Na⁺ ions, as indicated in Figure 7-5D and E. If one imagines this permeability being added to the K⁺permeable membrane of Figure 7-5C, an inward flow of Na⁺ ions results, driven not only by the interior negativity of the cell but also by the Na⁺ concentration gradient (Fig. 7-5D). The inward Na⁺ current would be small because the Na⁺ conductance is small, but it would nevertheless move positive charges into the cell, making its interior less negative. This in turn would cause the membrane potential to move slightly away from V_K, creating a small voltage gradient that drives K⁺ ions out of the cell. Assuming for a moment that concentrations remain constant, a steady state is reached in which the small inward Na⁺ current (small because the Na⁺ conductance is small) is exactly counterbalanced by a small outward K⁺ current (small because the conductance is relatively large but the voltage gradient is small). The exact membrane potential at this steady state is somewhere between V_K and V_Na, dictated by the relative magnitudes of the K⁺ and Na⁺ permeabilities (see Appendix 7B). Typical neurons have resting Na⁺ permeabilities that are 1% to 10% as great as the resting K⁺ permeability, so the resting membrane potential is a weighted average of V_K and V_Na, or around −65 mv (closer to V_K than to V_Na because of the greater K⁺ permeability).

Concentration Gradients Are Maintained by Membrane Proteins That Pump Ions

There is a major difference between the equilibrium condition that exists when the membrane is permeable to only one ion (Fig. 7-5C) and the steady state that is achieved when the membrane is permeable to more than one ion (Fig. 7-5E). In the equilibrium condition the equal and opposite current flows involve the same ion (e.g., K⁺), so no concentration changes ensue and no energy is required to maintain the condition. In the steady-state condition the equal and opposite current flows involve different ions and eventually result in concentration changes. In the typical neuronal situation, the small but constant inward Na⁺ and outward K⁺ currents, if uncompensated, would slowly dissipate the Na⁺ and K⁺ concentration gradients across the membrane. The equilibrium potential for ions with no concentration gradient is 0 mv, so the membrane potential would slowly fade away. Another class of membrane proteins called ion pumps allows this dilemma to be circumvented by neurons and, indeed, by all cells. The best studied of these is a membrane-spanning Na⁺/K⁺ ATPase, so called because it uses the energy released by hydrolysis of adenosine triphosphate (ATP) to move Na⁺ ions out of the cell and K⁺ into the cell (Fig. 7-5F). However, Ca²⁺ ions or Cl⁻ ions can also move into cells in response to certain kinds of stimuli, and specific membrane pumps are available to redistribute them as well. All of them pump at concentration-sensitive rates, so they speed up when there are more ions to be extruded or recaptured.

Inputs to Neurons Cause Slow, Local Potential Changes

We think of conventional electronic devices as designed not to distort but rather to transmit signals over long distances unchanged, accurately amplifying them as necessary. Neurons do not seem to be very well designed for transmitting information over long distances. Axons, relative to metal wires, are poor conductors; their insulation (except where myelin is present) is not very good, and the input signals to neurons become smeared out over space and time because of membrane resistance and capacitance. As will be seen in this chapter and the next, however, these apparent shortcomings are precisely what allow neurons to compare and summate numerous inputs and make determinations about appropriate outputs.

Changes in the relative permeability of the membrane to ions such as K⁺ and Na⁺ (and Ca²⁺ and Cl⁻) are the basis for electrical signaling by neurons. Increasing the Na⁺ permeability, for example, would cause an increased inward Na⁺ current and depolarization* of the membrane (i.e., decreased internal negativity). Increasing the K⁺ permeability would hyperpolarize the membrane (i.e., make the inside more negative by moving its potential even closer to V_K). Such permeability changes may be caused by the action of ligand-gated channels at postsynaptic sites (Chapter 8) or by the action of stimulus-gated channels in the membranes of sensory receptors (Chapter 9). In either case, the net effect is a change in current flow through the affected channels for as long as the probability of their being open remains altered. The consequences of local current flow such as this are dictated largely by the passive electrical properties of adjacent areas of neuronal membrane—their resistance and capacitance. These passive electrical properties are referred to as the cable properties of neurons.