(7.1)
Hard vertebrae have a much larger Young’s modulus than the soft dura mater, as a greater stress (about 100 times) is required to produce the same strain. The concept of elasticity is at the foundation of solid mechanics.
2.
The Frenchman Jean Louis Marie Poiseuille (1797–1869) was an experimental physiologist with formal training in mathematics and physics (Sutera and Skalak 1993). He was first interested in ‘the force of the aortic heart’ and so invented the U-tube mercury manometer to measure arterial blood pressure in horses and dogs. Continuing his study of haemodynamics, Poiseuille next turned his attention to the microcirculation. On observing frog mesenteric blood vessels, he noted that red cells would stream in the centre of the vessels, whereas white blood cells tended to stick to the vessel walls. To understand the nature of these flow patterns, he subsequently conducted an extensive series of experiments in small-diameter glass tubes. Fluid flows from high to low pressure, and Poiseuille established the relationship between the fall in driving pressure along the tube (Δp), the length (L) and diameter (D) of the tube and the subsequent volumetric flow rate (Q). The fluid property connecting these four quantities is the viscosity (μ), and their relation is known as Poiseuille’s law :
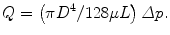
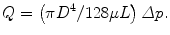
(7.2)
Thus, for a given pressure drop, there will be a greater volumetric flow rate through vessels having a larger diameter or a lower viscosity. Such differences come into play when we compare the calibres of subarachnoid and perivascular spaces and the viscosities of CSF and blood. Mathematics also gives us the converse relation, in that a greater drop in pressure will result from a larger flow rate.
7.2.3 Constructing a Mathematical Model
What mathematics is and its utility are widely misunderstood (Stewart 2011). Mathematics (Greek ‘máthēma’, to learn) is a branch of science that deals with concepts of quantity, space, structure and change. It is often referred to as the ‘language of nature’ for its ability to communicate the ideas of physical phenomena. Mathematics has symbols and a grammar for arranging them, but over and above a traditional language, it also includes a system of reasoning. We can explain equations in words but seldom the connection between them; herein lies the power of mathematics (Feynman 1965).
The first step in constructing a mathematical model is to decide upon the level of detail. It is not feasible to include every physical feature that influences the phenomenon being studied. Nor, in fact, is this desirable as doing so would only reproduce the complexity inside the ‘black box’ that we did not understand in the first place. The aim, therefore, is to retain the features with the greatest influence and omit the rest. Every mathematical model is thus a deliberate idealisation of the phenomenon being studied. Choosing what to include is a process of trial and error, guided by the intuition of experience and the comparison of predictions with empirical data (Barenblatt 2003). There is no one ‘correct’ model of a given system and what to include depends on the question being asked. A useful starting point is to eliminate quantities that are relatively ‘small’. For example, the vertebrae are very hard and stiff compared to the meninges and spinal cord, so their shape is much less affected by typical subarachnoid fluid pressures; in mathematical notation, ε bone will have a much smaller value than ε soft tissue. Thus, it may be reasonable to omit the elasticity of the vertebrae when, say, studying the effects of cough-based pressure pulses in the spinal canal. In contrast, if one were interested in spinal trauma, then the much higher forces involved would demand the bone be treated as an elastic material. By convention, mathematicians and engineers would tend to say “we assume the vertebrae are rigid”, rather than “we omit the elasticity of the vertebrae”; these statements mean the same thing, and what is being assumed is that omitting these features from the model so will not significantly change the outcome of subsequent calculations and predictions.
Once all of the simplifying assumptions have been made, one can write down a set of equations that govern the system. This is the essence of the mathematical model. The next task is to solve the equations, for which there are two choices: (1) solve them by hand using pen and paper or (2) solve them on a computer. The former is called an analytical solution and yields great insight into the underlying phenomenon by obtaining a relation describing it explicitly, e.g. Eq. (7.2). While this approach is preferable, it is usually only possible for the very simplest equations, so instead one often employs computer programs to obtain a numerical solution. Computers are digital so they can only store information as a set of discrete samples. As a result, solving an equation on a computer may introduce error due to the continuums of time and space being approximated as a finite number of values. The finer the partitioning, the smaller the error will be but also the more demanding it becomes to compute. Thus, compromise must be made.
To demonstrate that a mathematical model makes reliable predictions, it should be validated against empirical data. For example, Eq. (7.2) was derived mathematically from the laws of mechanics by Eduard Hagenbach (1860), and it matched the relationship that Poiseuille obtained from his glass-tube experiments (Sutera and Skalak 1993). Unfortunately, it is often the case with problems in biomechanics that a controlled experiment, equivalent to that of Poiseuille, is not possible. Instead, in these situations, one deconstructs the model into sufficiently general components, such as water flow through a pipe that can be validated separately. Solutions that are obtained via computer also need to be verified to ensure that no mistakes were made in the software; simpler versions of the equations can be computed and compared to well-known analytical solutions, such as the speed of pressure waves in a fluid-filled elastic tube (e.g. Cirovic and Kim 2012). Thus, validation ensures that the correct equations are being solved, while verification ensures that the equations are being solved correctly.
7.2.4 Modelling Predictions
The real usefulness of a mathematical model lies in its predictive capabilities. Once validated, a mathematical model can be used to determine what happens in hypothetical situations and, most prominently, situations that are not amenable to physical observation and measurement. For example, in a model of posttraumatic syringomyelia, the efficacy of various shunt treatments have been evaluated (Elliott et al. 2011). Crucially though, one must ensure that predictions are consistent with the assumptions upon which the model is based (Dym and Ivey 1980). For biological materials, the elasticity as defined in Eq. (7.1) is only applicable for small strains. This means that in a spinal canal model, one would likely have to choose small enough input pressures to ensure that this condition were not violated.
In clinical and animal studies, a sufficiently large cohort is required to make representative predictions. The empirical findings are analysed in terms of their statistical distribution (mean, standard deviation, confidence intervals, etc.) but may not be predicted precisely. In contrast, mathematical models based on Newton’s laws of mechanics are isolated from external influences, so there is no random variation, making them deterministic, rather than stochastic (Murthy et al. 1990). It is this ability to remove confounding factors that permits analysis with absolute certainty. However, it is a certainty limited to the model itself. The relevance of mathematical predictions to the biological system depends on the degree to which the model is representative of the biological system.
7.3 Mechanics of the Healthy Cerebrospinal System
7.3.1 Solid and Fluid Components
The spinal cord and brain constitute a soft, elastic solid that is housed within the rigid confines of the vertebral canal and cranial cavity. The intervening subarachnoid spaces, which also extend as cavities (ventricles) into the brain, are filled with cerebrospinal fluid (CSF), not unlike sea water. As the cord and brain themselves are also largely water by mass, they float within their bony container but are hitched in place, loosely by the arachnoid trabeculae and, in the case of the cord, more substantially by the denticulate ligaments and filum terminale (see Chap. 3). These elastic connections span the subarachnoid space which is lined by the pia mater along the cord and brain surface and by the arachnoid layer that is adherent to the dura mater that lines the vertebrae and skull (England and Wakeley 2006).
7.3.2 Elastic Properties of the Soft Tissues
The elasticity of any material is determined by its microstructure, and in the case of soft biological tissues, this largely means the quantity and arrangement of collagen and elastin fibres . The collagen protein molecule has a triple-helix structure, and when grouped into fibrils, and subsequently into fibres, it becomes a much stiffer structure than elastin fibres, which are rubbery, convoluted, thin strands (Fung 1993). The spinal dura mostly consists of collagen fibres, densely arranged in longitudinal bundles but with a network of fine elastin fibres threading in all directions (Tunturi 1977; Maikos et al. 2008). In contrast, the spinal pia consists of small bundles of collagenous fibres together with individual collagen and elastin fibres that are all loosely woven into a reticular pattern (Tunturi 1978). The spinal cord parenchyma itself has a negligible amount of collagen and elastin so its elasticity instead depends on the axonal fibres and their myelin sheaths.
Estimates of the Young’s moduli for dura, pia and the spinal cord vary widely in the literature, but broadly speaking, the dura is about 100 times stiffer than the pia (i.e. greater E), which in turn is about 100 times stiffer than the soft cord tissue (Elliott et al. 2013). These tissues, like all materials, can only withstand a certain amount of strain before they become permanently damaged; i.e. they no longer recover their original shape when the forces are removed and may, in fact, rupture. The stress corresponding to this ‘mechanical failure’ is referred to as the yield strength. Collagen, for example, has a Young’s modulus of 1–1.5 GPa,5 but as it can only withstand a strain of 10–20 %, its yield strength is much lower, 70–150 MPa (Meyers et al. 2008).6 The pia’s greater stiffness than the spinal cord to which it is attached limits the strain that the cord endures, thereby performing a mechanically protective role (Bertram 2010; Ozawa et al. 2004).
7.3.3 Fluid Pathways
CSF is secreted from the choroid plexus and commences a slow bulk flow from the ventricles, continuing through the subarachnoid space before the fluid is reabsorbed back into the superior sagittal sinus and venous system via the arachnoid villi. The total volume of CSF (about 150 ml) is replaced about three times daily (Bradbury 1993). Ill-defined amounts of CSF are also filtered from blood plasma and absorbed into the lymphatic system (Brodbelt and Stoodley 2007). In the human cranial subarachnoid space, the arteries and veins reside within pia -like tubular sheaths. The arterial sheaths continue into the brain parenchyma, while the veins lose their sheaths at the pia mater interface (Zhang et al. 1990). Although not proven, it seems likely that the situation is the same in the spinal canal. As the interstitial and cerebrospinal fluids may pass through pores and leaky gap junctions in the pia, the extracellular, perivascular and subarachnoid spaces thus form a single continuous fluid compartment (Rennels et al. 1985; Stoodley et al. 1996; Johanson 2008; Saadoun and Papadopoulos 2010). Superimposed on the bulk CSF flow is a reciprocating flow of more substantial magnitude—measurable with MRI—that is due to the periodic volume changes of the blood vessels with the cardiac and respiratory cycles.
7.3.4 Volume Compliance
The volume change of a distensible vessel is related to pressure change through compliance. However, there are two measures of compliance: static and dynamic (Bertram 2010).
Static compliance is defined as the change in vessel volume resulting from a given change in the pressure acting across the vessel walls:
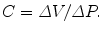
i.e. the slope of the volume versus pressure curve, with which most clinicians are familiar. In the main fluid compartment of the cerebrospinal system, the CSF reservoir, it is well established that static compliance is not constant but decreases as the compartment becomes distended. The cranial pressure-volume index (PVI)7 attempts to describe this filling-volume-dependent quantity with a single value (Marmarou et al. 1975). Heiss et al. (1999) measured the static compliance of the human craniospinal system as ranging between 3 and 15 ml/mmHg. Marmarou et al.’s (1975) measurements on cats suggest that the spinal canal contributes about a third of the total. Conceptualising the cerebrospinal system as collection of compartments (CSF, blood, brain, spinal cord) allows it to be expressed mathematically as a hydraulic lumped–parameter model. The compliance and flow resistance between adjacent compartments are ‘lumped at’ (assigned to) their interface; i.e. these properties are spatially averaged over each compartment and so do not vary within compartments. The solution consists of the discrete compartment pressures as they vary in time. This modelling technique has long been popular in studying disorders of the intracranial CSF system, such as hydrocephalus (e.g. Agarwal et al. 1969; Ambarki et al. 2007), but including intraspinal compartments to investigate syringomyelia has only been attempted in three studies (Chang and Nakagawa 2003, 2004; Elliott et al. 2011). The reason for this disparity is that it is easier to measure the inter-compartmental compliances and resistances of the head than the spinal canal. The cranial volume may be considered constant due to the rigidity of the skull, the so-called Monro-Kellie doctrine , which makes any internal volume (hence pressure) changes well defined. In the spinal canal, the dura mater is surrounded by fluid (distensible veins) and fatty tissue that are necessary for the mobility of the spine so the total compartment volume is variable.
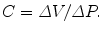
(7.3)
Dynamic compliance is a measure of how time–varying changes in pressure and volume are related, as in pulsation. It governs the speed of pressure waves which feature prominently in the spinal canal. A cough elevates the pressure in the thorax that squeezes blood from the thoracic veins into the adjacent epidural veins. Distension of these veins transmits pressure to the spinal subarachnoid space, leading to a travelling pressure wave (Lockey et al. 1975). Williams (1976) was the first to measure the speed of these waves using pressure transducers connected to lumbar puncture needles. A non-invasive technique, using MRI, has recently been developed (Kalata et al. 2009). Wave speeds are typically around 4 m/s.
The propagation of pressure waves in elastic, fluid-filled tubes is a well-studied problem of classical mechanics (Lamb 1898; Womersley 1955). The spinal cord may be thought of as an annular, elastic, solid cylinder, containing an inner cylindrical central canal and sheathed in a tube of pia mater, which in turn is surrounded by an annular cylinder of fluid, the spinal subarachnoid space that is contained by the outer tube of dura mater. A number of mathematical models of the spinal canal have been developed from variants of this system of coaxial tubes (Lockey et al. 1975; Loth et al. 2001; Berkouk et al. 2003; Carpenter et al. 2003; Bertram et al. 2005, 2008; Cirovic 2009; Elliott et al. 2009; Bertram 2009, 2010; Martin et al. 2012; Cirovic and Kim 2012; Elliott 2012; Cheng et al. 2012), elucidating the mechanics of a number of wave modalities.
The wave recorded by Williams (1976), normally described as the ‘CSF pulse wave ’ or the ‘subarachnoid pressure wave’, is made up of a moving section of cord constriction and an adjacent segment of dura distension. Of the known wave types, this one involves the largest cord motion and so is most easily observed with MRI. Another wave exists in which the cord distends, rather than constricts, but this vanishes as the central canal is obliterated by adulthood (Milhorat et al. 1994). The healthy spinal canal supports at least two further waves, one similar to the previous but also involving lengthwise cord compression and a final wave, almost exclusively involving stretching of the dura (Cirovic 2009; Bertram 2009; Cirovic and Kim 2012). A cough will initiate a pressure pulse in the thoracolumbar region which will set up each of the above wave types in pairs, one wave travelling in the rostral direction and the other in the caudal direction (analogous to the way surface waves radiate from a stone dropped into a pond). These waves will successively reflect at the craniocervical junction and the lumbar cistern, respectively, and vice versa. This may amplify the fluid pressure, and tissue stresses in regions where opposite-moving wave components superimpose. Individual waves will not persist indefinitely though. The motion of fluid and solid spinal components involves kinetic energy (Greek kinētikos, ‘to move’) that will be lost to internal friction. This friction is termed viscosity 8 in fluids and viscoelasticity in solids and is responsible for attenuating waves as they travel. Getting the speed of the CSF pulse wave in a mathematical model to match that measured in the human body has become a useful way of validating the model as it ensures that the dynamic compliance is anatomically realistic.
Although pressure waves are induced by abrupt percussive events, they do not induce a significant amount of CSF motion in the spinal subarachnoid space. The alterations in the shape of the cord and dura occur too quickly for the fluid to keep up so the tissue only has a ‘massaging’ effect, gently stirring the fluid into motion (Bertram 2009). The reciprocating motion of CSF, well known to the clinician, is due to the lower-frequency pulsations of the cardiac cycle (Bertram 2010). The interdependence of pressure drop and flow rate means that the pressure drop along the spinal subarachnoid space changes from positive to negative, and vice versa, twice per cardiac cycle.
7.4 Mechanics of Syringomyelia
7.4.1 Syrinxes
Mechanically, syrinxes provide the cord with additional localised compliance through displacement of the contained fluid when the syrinx is squeezed into a different shape. Williams (1980) hypothesised that a CSF pulse wave would compress the syrinx at one end, causing the fluid to ‘slosh’ to the other end, akin to squeezing a water balloon, with the syrinx subsequently extending by tissue dissection. In a computer-based mathematical model, Bertram (2009) demonstrated that a CSF pulse wave travelling rostrocaudally induces axial motion of the syrinx fluid relative to the syrinx walls, leading to fluid pressure at the caudal end of the syrinx exceeding spinal subarachnoid space pressure at the same level, and a distending (tensile) stress at the caudal tip of the syrinx wall. The pulse wave slowed down as it passed the syrinx, agreeing with Cirovic’s (2009) analytical prediction, but not enough to induce the substantial sloshing motions of syrinx fluid proposed by Williams. Consequently, the incurred stress had relatively little potential for tearing the cord tissue and concomitant lengthening of the syrinx. It was acknowledged, though, that a higher-resolution model of the spinal cord is needed to better capture the large stress gradients at the ends of the syrinx.
An additional complication arises with the presence of a syrinx—partial wave reflection and refraction. When a pressure wave reaches a syrinx border, some of the wave continues ahead, and the remainder doubles back due to the change in cross-sectional constitution. Given that there are many types of wave, all moving at different speeds, and that overlapping waves sum together (either reinforcing or cancelling each other), the resulting state of fluid pressure/velocity and tissue stress/displacement easily becomes complicated (e.g. see figure 10 in Bertram 2009). This, unfortunately, does not lend the wave mechanics to intuitive theorising, and some wave-based theories, while being admirable attempts to explain the pathophysiology of syrinx filling, are conceptually unphysical (e.g. Greitz 2006).
7.4.2 Syrinxes with Associated CSF Obstruction
Stenosis occurs at the craniocervical junction in the presence of a herniated hindbrain. It also occurs elsewhere along the spinal subarachnoid space due to, most commonly, scar tissue build-up following spinal trauma. These pathologies obstruct the CSF circulation and act as amplification sites for pressure and stress through the wave reflections that they produce. Their frequent juxtaposition with syrinxes has motivated several groups to pursue a mathematical line of enquiry (Berkouk et al. 2003; Carpenter et al. 2003; Bertram et al. 2005; Elliott et al. 2009; Bertram 2010; Cirovic and Kim 2012; Elliott 2012).
Carpenter and colleagues developed a pathogenesis hypothesis based on the theory of shockwaves (Berkouk et al. 2003; Carpenter et al. 2003). They demonstrated in a mathematical model of coaxial tubes that a pulse wave will become steeper as it propagates, much like a beach wave does on reaching shallow water. If the concomitant elevation in pressure difference between the spinal subarachnoid space and the cord/syrinx reaches the maximal value, then a so-called shock-like elastic jump occurs, which is mathematically similar to the beach wave breaking. When this pressure wave reaches a complete stenosis, the incident and reflected components superimpose, creating an abnormally large tissue stress/syrinx pressure that could potentially damage the cord/expand a syrinx. Although the predictions make a fundamental contribution to the mathematical modelling community, subsequent analysis reveals that the proposed mechanism is unlikely to play a role in the human body; the gross dimensions of the spinal canal and its contents only confer marginal shock-like stress/pressure changes (Elliott et al. 2009). When additional features are included in the coaxial tube representation of the spinal system, such as fluid viscosity and the ability to capture a spectrum of frequencies, shock-like phenomena become even less likely. The pressure waves tend to spread out and attenuate rather than steepen and amplify (Bertram et al. 2005).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








