Motor Systems
Motor systems are intrinsically rather more complex than sensory ones, which is one reason why we know rather less about them. Where do these complexities come from?
Why studying motor systems is difficult
An obvious way to study the motor system, by analogy with recording from sensory systems, is to stimulate various bits and see what happens. But – as we noted in Chapter 1 – there is a difficulty about doing this: how do we know what is an appropriate pattern of stimulation to apply in order to get a response?
A further difficulty in using stimulation to study the motor system is that whereas sensory systems by and large progress in a straightforward way from level to level, a characteristic of motor control is that every action necessarily results in sensory feedback. Lift your hand: immediately, a torrent of sensory activity floods back into the brain, from the skin, from muscle and joint receptors, from vision and the other special senses. This makes the effects of stimulating a particular region of the motor system additionally complex: any movement that may result from it also generates new patterns of afferent activity. By acting on centres whose descending activity then influences that region, this messes things up by altering the pattern of stimulation we are trying to apply.
For both these reasons, electrical stimulation has not been as helpful a way of studying the motor system as one might have thought. A more fruitful approach has been an extension of the methods that have been successful in probing sensory systems. We apply ‘real’ stimuli to the senses, and trace the resultant patterns of activity as they penetrate deeper and deeper through the levels of the nervous system and emerge triumphantly again at the motor end as movements. In systems as complex as those controlling the human hand, this is not yet technically feasible. But where the number of levels is much smaller, as in more primitive brains like those of insects, or in simpler sub-systems of the mammalian brain (like those controlling eye movements, which may have as few as three neuronal levels between input and output) this approach has taught us a great deal.
One general lesson we have learnt is how much more can be discovered about the brain by studying complete systems with an output, compared with purely sensory systems. The visual system is a good example. When people first started exploring it with microelectrodes, at first everything went swimmingly: going systematically from layer to layer into the cortex, investigators such as Hubel and Wiesel found a clear logical progression from ganglion cells to simple cells and to complex cells. People confidently expected this trend to continue, and that after line detectors we would discover square detectors and circle detectors and A detectors and teacup detectors… but they didn’t; visual neurophysiology began increasingly to lose its way. Why? Because investigating a sensory system without a clear sense of what it is for is like trying to understand a television without knowing that it is meant to show pictures. We may think it is ‘for’ perception; but since we have no idea what perception is (or any other aspect of consciousness) it is hardly surprising if we end up bewildered and lost. But once we start looking at systems that actually do something tangible, we make progress.
Motor control and feedback
Feedback means using information about results to improve performance, and feedback from the effects of motor responses is fundamentally important in the control of movement. A good way to begin a study of the motor system is to consider the ways in which this sensory information might in principle be used.
No feedback: ballistic control
There are many circumstances when our motor systems are forced to act blindly because for one reason or another they are deprived of normal sensory feedback. When I nonchalantly toss some orange-peel into a waste bin, once it has left my hand, no amount of sensory feedback
about its trajectory is going to enable me to modify its flight. I have clearly had to work out beforehand the precise sequence of motor commands necessary in order to produce the correct pattern of muscular contractions that I need to achieve my goal. Sometimes this kind of blind behaviour can extend to the overall result of the movement as well as the details of its execution. A classic example is the nest-building behaviour of the brown rat, described by Konrad Lorenz. Having decided to build a nest, it performs a stereotyped series of actions: it runs out to get nesting material, drags it back to the centre of the nest, sits down and forms it into a sort of circular rampart, pats it down and smoothes it, then runs out to get more material; and so on until the nest is finished.
about its trajectory is going to enable me to modify its flight. I have clearly had to work out beforehand the precise sequence of motor commands necessary in order to produce the correct pattern of muscular contractions that I need to achieve my goal. Sometimes this kind of blind behaviour can extend to the overall result of the movement as well as the details of its execution. A classic example is the nest-building behaviour of the brown rat, described by Konrad Lorenz. Having decided to build a nest, it performs a stereotyped series of actions: it runs out to get nesting material, drags it back to the centre of the nest, sits down and forms it into a sort of circular rampart, pats it down and smoothes it, then runs out to get more material; and so on until the nest is finished.

This certainly looks like the intelligent behaviour of an animal that is aware of the consequence of its actions: yet a simple experiment shows it to be nothing of the kind. If it is not given enough to make a nest, the rat still runs out to grab the (non-existent) material, and goes through the motions of dragging it back, forming it into a rampart and patting and smoothing it, even though in reality there is nothing there. Feedback, in other words, was not in fact being used. And of course we ourselves have all had the experience of carrying out some equally skilled and complex series of actions – making tea, for example – and have embarrassingly revealed its stereotyped, robotic nature by absent-mindedly putting coffee instead of tea into the teapot.
Motor acts of this general type are called ballistic – a word meaning ‘thrown’ – and the way in which they are controlled is best thought of in terms of a diagram like the one below. These kinds of diagrams are central to understanding control systems, and to appreciate them fully we need to get to grips with a certain amount of rather unattractive jargon. 

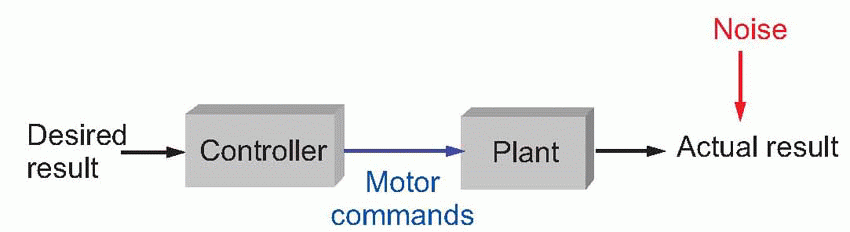 |
Here we start with the desired result or goal, in this case that we want the orange-peel in the bin. This is translated by a controller into an appropriate pattern of commands. These commands produce the actual result through their effect on what engineers call the plant – the thing that is being controlled, in this case, the body’s muscles. If the controller is functioning properly, then the actual result will equal the desired result: the peel will end up in the bin. How well all this works depends on how good the controller is: the more it knows about how the plant will behave in response to any particular command, the better it will perform. So it needs something like a library of motor programs suitable for different acts, where it can look up the rules needed to translate a particular desire into an appropriate command.
A well-known example of such a system is in the control of ballistic missiles. Here the desired result is the destruction of some displeasing portion of the globe; computations are then made, based on knowledge of the missile’s characteristics, to determine such parameters as what direction to point it in and how large a thrust is required at take-off: but once it is launched no further action can be taken beyond hoping that the calculations were in fact correct.
Ballistic control is conceptually simple, but it has a fatal defect: it is helplessly vulnerable to what systems engineers call noise. Noise is any kind of unpredictable disturbance that makes the actual result different from what the controller expects. If the wind happens to be blowing the wrong way, our ballistic missile may arrive somewhere embarrassing and cause a diplomatic incident. Because the world we live in is never entirely predictable – nothing is certain – a given set of motor commands will never produce quite the same result twice running. A particular pattern of activity in motor nerves will produce different movements of a limb on different occasions, depending on a host of internal factors: body temperature, fatigue, the amount of energy available, and so on. Even more important in motor systems is the effect of load. When we use our limbs to shift things around, carrying or throwing, a given degree of muscle activity will generate quite different movements, depending whether we are dealing with a lump of rock or a feather. As we shall see, most of the lower levels that control the limbs are devoted to solving this problem of achieving the movements we want despite the noise introduced by unpredictable loads.
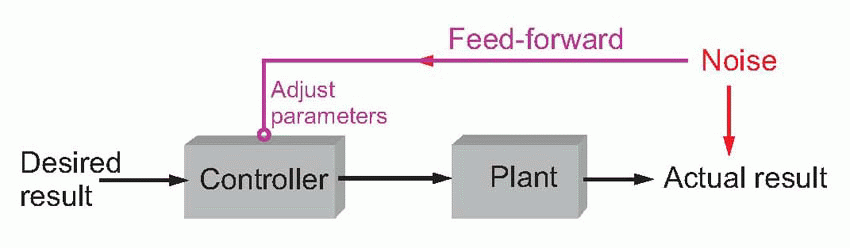
Parametric adjustment: feed-forward and feedback
One way of dealing with noise is to have some kind of sensor that monitors the noise before it affects the system, and to use this information to adjust the parameters of the controller to allow for it. This kind of modification of the controller parameters to anticipate the effects of noise is called parametric feed-forward. If we measure the speed of the wind before we launch our missile, we can allow for its disturbing effects, just as marksmen adjust their sights to allow for deviation by the wind. Much sensory information is used by the brain in this way, especially in making allowance for the effects of different loads.
We shall see later that the neural circuits controlling muscle length use information from force-detectors in the skin and tendons that monitor load in order to make appropriate adjustments of motor commands.
We shall see later that the neural circuits controlling muscle length use information from force-detectors in the skin and tendons that monitor load in order to make appropriate adjustments of motor commands.
 |
But even this approach is doomed to failure. In general there are infinitely many things that might cause perturbations, and the brain clearly cannot have a plan for dealing with every one of them in advance. Instead of trying to anticipate absolutely everything that might possibly occur, one solution is to take a more pragmatic approach, with a system that learns from its own mistakes, using not feed-forward but parametric feedback. This introduces two exciting new pieces of jargon: a comparator (the circle with two converging arrows) compares the actual result with the desired result by subtracting one from the other, and it generates an error signal that is used to modify the controller’s parameters. In general, the error signal is a measure of how well the system is coping: if it is zero, the controller is doing a good job, and there is no reason to change its parameters. If the system keeps on making a mess of things, generating persistent error signals, then the commands are gradually adjusted until it gets it right. The advantage of this approach is its flexibility. Rather than requiring stored programs ready in advance for any conceivable kind of action, by starting with rather simple, all-purpose programs, one may refine, through trial and error, what is needed for the tasks that are actually encountered.
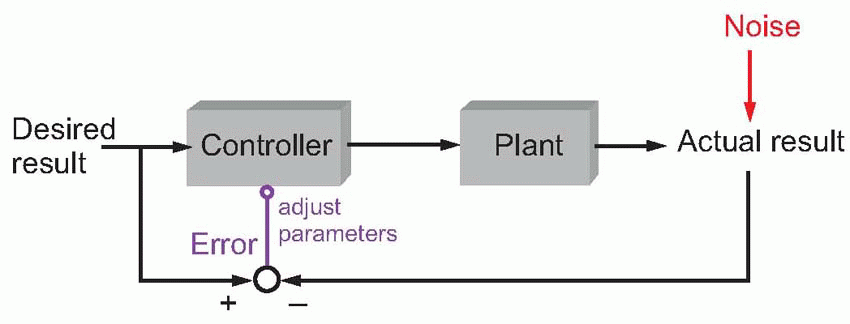 |
It goes without saying that this kind of behaviour – using error information from one attempt to improve performance on the next – is highly characteristic of the way in which our motor systems learn to execute complex actions. In playing darts, a novice may at first use preexisting programs developed perhaps from his experience of throwing other objects such as cricket balls, no doubt ultimately from throwing rattles out of his pram. But as he practises, though the feedback from each throw obviously arrives too late to use immediately, it is used to reduce future errors, and in the end he may gradually evolve very accurate programs specifically for dart-throwing. A great deal of the learning of motor skills can usefully be thought of as a parametric feedback of this kind, in which errors are used to modify our stored motor programs.
A specific example, discussed in more detail in Chapter 11, is the vestibulo-ocular reflex.  When we move our head, signals from the semicircular canals are used to drive the eyes by an equal amount in the opposite direction. As a result, they maintain the direction of gaze in space and the retinal image of the outside world remains relatively fixed. This is clearly a ballistic system. Equally clearly, it will go off the rails if the performance of the muscles is degraded through fatigue or disease, or if there is some malfunctioning of the canals. In fact it turns out that the reflex is continually adjusted to ensure that the eye movements really are equal and opposite to the head movement. The error signal in this case comes from neurons that respond to movement of the visual image across the retina; for this retinal slip only occurs when head and eye movement are not matched.
When we move our head, signals from the semicircular canals are used to drive the eyes by an equal amount in the opposite direction. As a result, they maintain the direction of gaze in space and the retinal image of the outside world remains relatively fixed. This is clearly a ballistic system. Equally clearly, it will go off the rails if the performance of the muscles is degraded through fatigue or disease, or if there is some malfunctioning of the canals. In fact it turns out that the reflex is continually adjusted to ensure that the eye movements really are equal and opposite to the head movement. The error signal in this case comes from neurons that respond to movement of the visual image across the retina; for this retinal slip only occurs when head and eye movement are not matched.
 When we move our head, signals from the semicircular canals are used to drive the eyes by an equal amount in the opposite direction. As a result, they maintain the direction of gaze in space and the retinal image of the outside world remains relatively fixed. This is clearly a ballistic system. Equally clearly, it will go off the rails if the performance of the muscles is degraded through fatigue or disease, or if there is some malfunctioning of the canals. In fact it turns out that the reflex is continually adjusted to ensure that the eye movements really are equal and opposite to the head movement. The error signal in this case comes from neurons that respond to movement of the visual image across the retina; for this retinal slip only occurs when head and eye movement are not matched.
When we move our head, signals from the semicircular canals are used to drive the eyes by an equal amount in the opposite direction. As a result, they maintain the direction of gaze in space and the retinal image of the outside world remains relatively fixed. This is clearly a ballistic system. Equally clearly, it will go off the rails if the performance of the muscles is degraded through fatigue or disease, or if there is some malfunctioning of the canals. In fact it turns out that the reflex is continually adjusted to ensure that the eye movements really are equal and opposite to the head movement. The error signal in this case comes from neurons that respond to movement of the visual image across the retina; for this retinal slip only occurs when head and eye movement are not matched.Though parametric feedback and feed-forward can vastly improve the performance of ballistic systems, they are still not ideal. In the first place, the calculations that are needed before the action takes place are in general extremely complex – even throwing orange-peel into a bin requires, in effect, the solution of a set of partial differential equations with countless variables – and it is not altogether plausible that the brain could actually have at its disposal a library of such routines so vast as to be able to deal with all the possible motor tasks it might ever encounter during its lifetime. The controller needs to have acquired knowledge about how the plant will behave in response to any kind of command sent to it, and keep this information up to date. So it needs memory as well as intelligence. In addition, parametric feedback only corrects after the event, by which time it may be too late. But there is another approach, much simpler and often better: direct feedback.
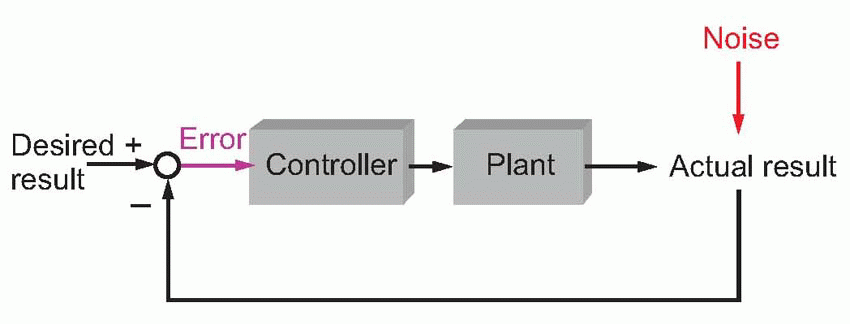
Direct feedback: guided control
Here we start, as before, with a desired result that we compare at every moment with the actual result. But now the error signal, instead of being used to tweak the parameters, is used directly as the input to the controller. Thus errors immediately generate motor commands that reduce the difference between the desired and actual result; this is the same kind of negative feedback system that underlies so many of the homeostatic mechanisms of ordinary physiology. Guided missiles are controlled by systems of this type: here the error signal might be something like the angle between the direction in which the missile is pointing and the direction of its target. Whereas a ballistic missile malfunctions disastrously
when the wind blows, a guided missile notes the effect of the wind on its relation to the target, and automatically corrects itself. When things go wrong, ballistic systems stay wrong, parametric ones gradually get better, and guided systems readjust immediately.
when the wind blows, a guided missile notes the effect of the wind on its relation to the target, and automatically corrects itself. When things go wrong, ballistic systems stay wrong, parametric ones gradually get better, and guided systems readjust immediately.
 |
In a guided system, instead of having to calculate what to do, you need only specify what you want. Like a welltrained servant, the system does all the rest by itself: such control systems are often called servo systems. Another advantage is that when errors arise, the computation of the correcting commands is in general very much simpler than the calculations needed in a ballistic system. A familiar example is a domestic central heating system, where the thermostat is the comparator, and generates an error signal which consists very simply of one of just two possible messages: either that the actual temperature is above what is wanted, or alternatively that it is below it – too hot or too cold. The subsequent computations of the motor commands could hardly be simpler: in the former case the boiler is switched off, in the latter case it is switched on. Another, physiological, example also illustrates this essential simplicity of guided systems. If we instruct a subject to look at a small light such as A and then suddenly move it closer to his nose as at B, we find that his eyes converge smoothly and quite quickly in such a way that in the end the image of the light still falls exactly on the fovea of each retina. The velocity of the convergence movement is high at first, but declines exponentially as the eye gets closer and closer to its target. This is just what would be expected of a guided system, in which the eyes are essentially driven by an error signal.
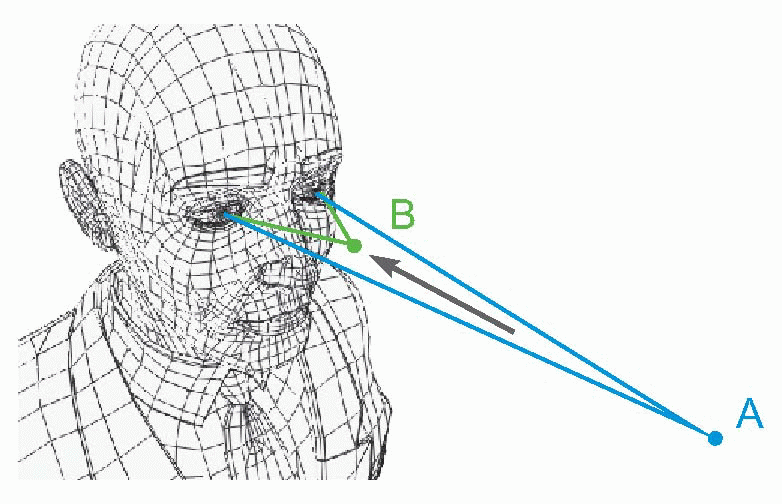 |
It turns out that this is indeed what is happening, and disparity between the two retinal images, sensed by cortical detectors of the kind described in Chapter 7, provides the error signal which generates the convergence. Experiments show that velocity of the eyes has a very simple relation to the size of this error: it is simply proportional. So as the eyes approach their goal, this error gets smaller, and the rate of movement correspondingly declines to zero: hence the time-course of the movement is roughly exponential. Direct feedback is intrinsically a simple process. 

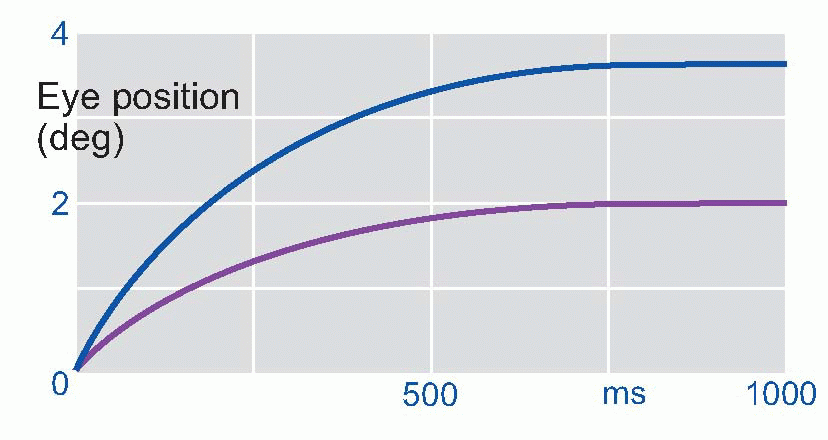 |
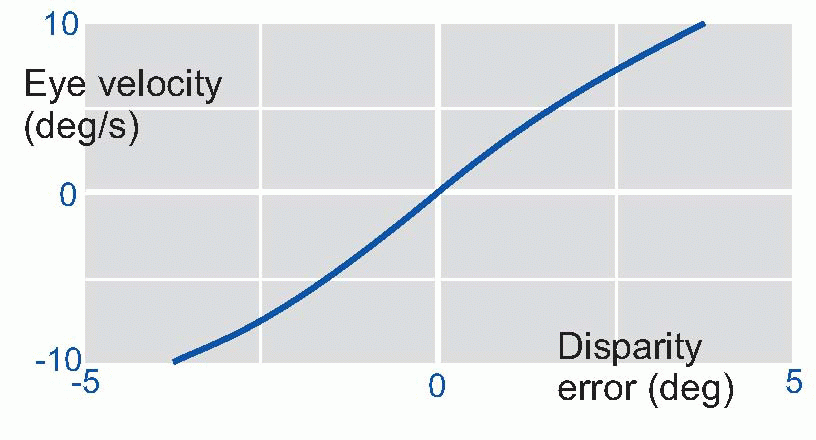 |
The overwhelming advantage of guided systems, however, is not so much their simplicity, but rather the fact that they are almost immune to the effects of noise. For if something unexpected happens that upsets the normal relationship between command and performance, this will be noticed at once (because it will generate error) and the system will instantly generate appropriate commands to achieve the desired result despite the existence of the disturbance. If you leave all the windows in your house open, the thermostat will at once sense the sudden drop in temperature, and the boiler will automatically be switched on until the temperature reaches the desired level once more. Thus the power and elegance of the system are that it guarantees to achieve what it has been designed to achieve, even when upset by types of interference that could not have been anticipated by its creator – including faults in the system itself (like the boiler furring up); it is capable of producing results that look intelligent even though – in sharp contrast to the ballistic system with its library of programs for different occasions – it knows very little (only the size of the error) and remembers nothing.
So why are all control systems not of this type? The reason is that direct feedback has a weakness. Its proper functioning depends critically on communicating information about the progress of the action rapidly to the comparator. In neural systems, both the sensory transduction and the consequent transmission may be rather slow, clearly a serious problem when trying to control fast movements. Delay of this kind ‘round the loop’ means that instead of responding to the error as it actually is, the system will be responding to the error as it was, however many milliseconds it takes for the information to find its way back to the brain. As a result, direct feedback systems have a tendency to show constant oscillations: if the feedback is turned at off at the moment the sensed error reaches zero, there will be an overshoot
in the opposite direction, requiring further correction, and so on: this is called hunting, and is obvious for example in ordinary domestic central heating systems. One way to get round it is to monitor not just the actual error x at any moment, but also the rate dx/dt at which it is changing, rather as the captain of a supertanker might stop the engines long before it reaches its berth, using the rate of slowing to predict where it will come to a halt. As can be seen in the figure above, (x + T dx/dt) is a good estimate of what the error will be at a time T in the future, so that if we make T equal to the time taken for observed corrections to have an effect, we can – to a first approximation – avoid these oscillatory responses. A good example of this (see p. 99) is in the Ia fibres from muscle spindles, which do indeed respond partly to error and partly to its rate of change, and for which T is roughly the time taken for information to be sensed and acted on.
in the opposite direction, requiring further correction, and so on: this is called hunting, and is obvious for example in ordinary domestic central heating systems. One way to get round it is to monitor not just the actual error x at any moment, but also the rate dx/dt at which it is changing, rather as the captain of a supertanker might stop the engines long before it reaches its berth, using the rate of slowing to predict where it will come to a halt. As can be seen in the figure above, (x + T dx/dt) is a good estimate of what the error will be at a time T in the future, so that if we make T equal to the time taken for observed corrections to have an effect, we can – to a first approximation – avoid these oscillatory responses. A good example of this (see p. 99) is in the Ia fibres from muscle spindles, which do indeed respond partly to error and partly to its rate of change, and for which T is roughly the time taken for information to be sensed and acted on.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree








